秋名山码民的主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
🙏作者水平有限,如发现错误,还请私信或者评论区留言!
目录
- 一、欧几里得
- 二、扩展欧几里得
- 三、算术基本定理
- 四、线性筛选求质数
- 五、等差数列
- 六、等比数列
- 七、组合计数
- 最后
一、欧几里得
求最大公约数的一种常用方法
public static int gcd(int a, int b) {
return b != 0 ? gcd(b, a % b) : a;
}
二、扩展欧几里得
求x,y使得ax+by = gcd(a,b)
public static int exGcd(int a,int b,int x,int y){
if(b == 0){
x = 1;
y = 0;
return a;
}
int d = exGcd(b,a%b,y,x);
y -= (a/b)*x;
return d;
}
三、算术基本定理
算术基本定理,又称为正整数的唯一分解定理,即:每个大于1的自然数,要么本身就是质数,要么可以写为2个或以上的质数的积,而且这些质因子按大小排列之后,写法仅有一种方式。

证明参考:维基百科
四、线性筛选求质数
在O(N)的时间复杂度内,求出来1 ~ n中所有的质数,以及每一个数的最小质因子。
private static void get_primes(int n) {
for (int i = 2; i <= n; i++) {
if (!st[i]) primes[cnt++] = i;
for (int j = 0; primes[j] * i <= n; j++) {
/*
因为prime中素数是递增的,所以如果i%prime[j]!=0代表i的最小质因数还没有找到,
即i的最小质因数大于prime[j]
也就是说prime[j]就是i*prime[j]的最小质因数,于是i*prime[j]被它的最小质因数筛掉了
*/
st[primes[j] * i] = true; // 把质数的i倍筛掉
/*
如果当i%prime[j]==0时,代表i的最小质因数是prime[j],
那么i*prime[j+k](k>0)这个合数的最小质因数就不是prime[j+k]而是prime[j]了
所以i*prime[j+k]应该被prime[j]筛掉,而不是后续的prime[j+k],于是在此时break
*/
if (i % primes[j] == 0) break; // 通过最小质因子来筛
}
}
}
五、等差数列
这俩个数列,学过高中数学的应该都清楚,我就不加以证明了。
1246. 等差数列
import java.util.Arrays;
import java.util.Scanner;
/**
* @Author 秋名山码神
* @Date 2023/2/17
* @Description
*/
public class Main {
static int N = 100010;
static int[] a = new int[N];
public static int gcd(int a,int b){
return b != 0 ? gcd(b,a%b) : a;
//b!=0 , 递归计算gcd(b,a%b)
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for(int i = 0; i<n; i++)
a[i] = sc.nextInt();
Arrays.sort(a,0,n);
int d = 0;
for(int i = 1; i<n; i++)
d = gcd(d,a[i] - a[0]);
if(d == 0){
System.out.println(n);
}else {
System.out.println((a[n-1] - a[0]) / d + 1);
}
}
}
六、等比数列
P8636 蓝桥杯 2016 省 AB 最大比例
#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
typedef long long LL;
LL x[N],a[N],b[N];
int cnt=0;
//假设原数列为 a,a*(p/q)^1,a*(p/q)^2,...,a*(p/q)^(n-1)
//假设抽取的数列 b0,b1,...,b(N-1) (从小到大排好序了)
// b1/b0,b2/b0,...,b(N-1)/b0--> (p/q)^x1,(p/q)^x2,...,(p/q)^x(N-1)
// 我们要求的是: (p/q)^k (p/q)>1,所以使k最大,即求 x1~x(N-1)的最大公约数
//这里我们使用更相减损术,因为我们没有得到确切的x1~x(N-1)是多少,我们只有(p/q)^x1,(p/q)^x2,...,(p/q)^x(N-1)这些的值
/*更相减损术:第一步:任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。
则第一步中约掉的若干个2的积与第二步中等数的乘积就是所求的最大公约数。*/
//更相减损术总用较大的减去较小的
/*例子:
98-63=35
63-35=28
35-28=7
28-7=21
21-7=14
14-7=7
所以,98和63的最大公约数等于7。*/
//我们这里要用更相减损术的是指数,所以要让(p/q)^x1,(p/q)^x2,...,(p/q)^x(N-1),两两计算,互除,除到结果为1,即x1=x2,此时幂次为0,结果为1,这其实就是y总的思路,再次感叹y总的才华
//把分子分母分别去算,结果是相同的因为,分子分母的幂次是相同的
LL gcd(LL a,LL b)
{
return b? gcd(b,a%b):a;
}
LL gcd_sub(LL a,LL b)
{
if(a<b) swap(a,b); //更相减损术总是大减小(它们的底数是一样的)
if(b==1) return a;
return gcd_sub(b,a/b);
}
int main()
{
int n;
cin>>n;
for(int i=0; i<n; i++) scanf("%lld",&x[i]);
sort(x,x+n);
for(int i=1; i<n; i++)
{
if(x[i] != x[i-1])
{
LL d=gcd(x[i],x[0]);
a[cnt]=x[i] / d; //得到x[i]/x[0]的分子
b[cnt]=x[0] / d; //得到x[i]/x[0]的分母
cnt++;
}
}
LL up=a[0],down=b[0];
for(int i=1; i<cnt; i++)
{
up=gcd_sub(up,a[i]); //两两求最大公约数
down=gcd_sub(down,b[i]);
}
cout<<up<<"/"<<down<<endl;
return 0;
}
七、组合计数
加法原理 : 若完成一件事的方法有n类,其中第i类方法包括ai种不同的方法,且这些方法互不重合,则完成这件事共有a1+a2+…+an种不同的方法。
乘法原理 :若完成一件事,需要n个步骤,其中第i个步骤有ai种不同的完成方法,且这些步骤互不干扰,则完成这件事共有a1a2…*an种不同的方法
排列数 : 从n个不同的元素中依次取出m个元素排成一列,产生的不同排列的数量为:

组合数 : 从n个元素中取出m个元素组成一个集合(不考虑顺序),产生的不同集合的数量为:
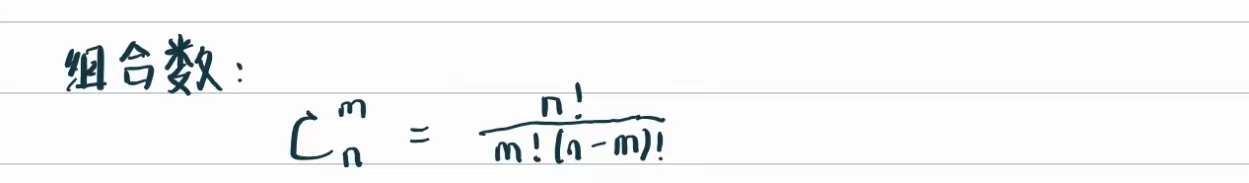
计算系数
//杨辉三角做法:
#include<iostream>
using namespace std;
long long x[1010][1010];
int main()
{
long long a,b,k,n,m;
cin>>a>>b>>k>>n>>m;
x[1][1]=1;
for(int i=2;i<=k+1;i++) for(int j=1;j<=i;j++)
x[i][j]=(x[i-1][j-1]*b+x[i-1][j]*a)%10007;
cout<<x[k+1][m+1];
return 0;
}
二项式做法
最后
数论的知识太多了,这是我最近三天想到的,后续有时间再补充吧!


![[蓝桥杯] 递归与递推习题训练](https://img-blog.csdnimg.cn/b32c0fab104b42f98cf30eca296850dc.png)