1、题目描述
设计一个结构包含如下三个方法:
void add(int index, int num); //把num加入到index位置
int get(int index); //取出index位置的值(是自然序的index位置,非排序后)
void remove(int index); //把index位置上的值删除
要求三个方法时间复杂度 O ( l o g N ) O(logN) O(logN)
2、思路分析
ArrayList 中删除一个元素需要将其后的元素全部往前移动一位,时间复杂度为
O
(
N
)
O(N)
O(N);LinkedList 中虽然删除一个元素的时间复杂度很低
O
(
1
)
O(1)
O(1),但是要找到这个待删除的元素得从头开始遍历,所以整体时间复杂度仍然为
O
(
N
)
O(N)
O(N)。
脚本语言中使用的“数组”好像什么功能都能完成,且很高效,是因为该数组底层并不是单纯的数组或双链表,只是高度改进后起名为“数组”。
题目补充说明:add(int index, int num) 方法在 index 位置加入 num,意思是假设原数组是 [3, 5, 2, 4],如果在 1 位置加入 7,则数组变成 [3, 7, 5, 2, 4]。
使用有序表可以设计出题目要求的复杂度的三个方法的结构。但是要注意:
-
为了区分值相同的两个数,在外面再封装一层。也就是说如果有多个相同的值,在树上就会有多个值相同的节点,通过内存地址区分开。每个节点记录的
size就是平衡因子,即以该节点为根的树上的节点个数。 -
改进的有序表并不是按照 key 进行排序的,而是按照自然时序。即当前节点的左树的自然时序都早于当前节点,右树的自然时序都晚于当前节点。
-
如果能维持一个以自然时序排列的树,无论左旋还是右旋,自然时序都维持正确,即不会改变这些数的相对次序。
-
对于一棵已经生成的树,加入新的数后无论如何旋转都不会改变它的相对次序,那么新加入的数应该挂在树的哪个位置上呢?
以自然时序排列组织的树 以及 旋转后相对次序没有发生改变 举例:
输入的数依次为[5, 3, 5]

再举例add 和 remove 操作:
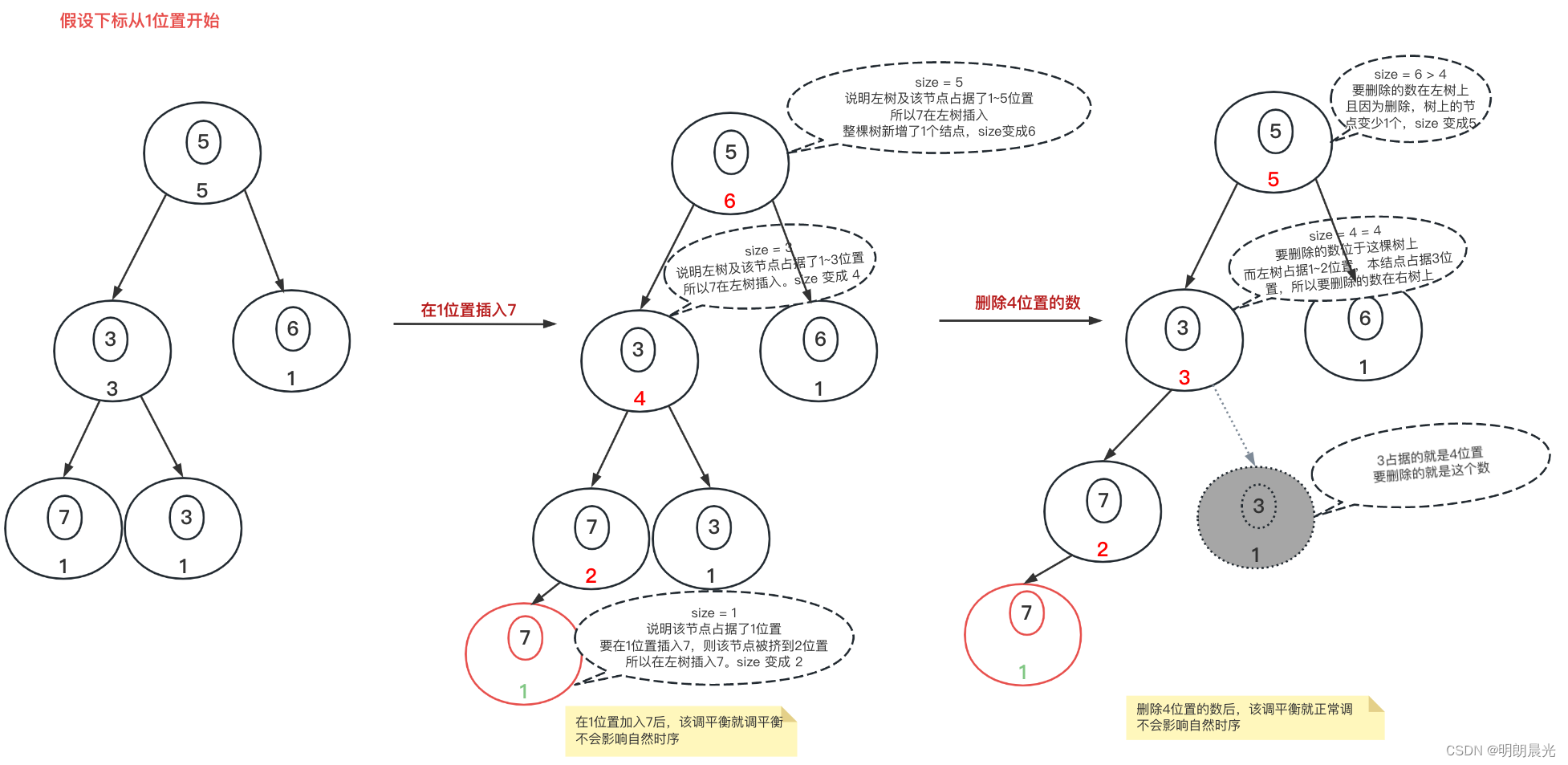
删除4位置的数后的树对应的自然时序就是[7, 7, 3, 5, 6]。
3、代码实现
import java.util.ArrayList;
//本质就是不去重版本的有序表/Size Balanced Tree
public class AddRemoveGetIndexGreat {
//没有key,因为参与排序的并不是key,而是隐含的自然时序
public static class SBTNode<V> {
public V value;
public SBTNode<V> l;
public SBTNode<V> r;
public int size; //平衡因子,也参与业务
public SBTNode(V v) {
value = v;
size = 1;
}
}
public static class SbtList<V> {
private SBTNode<V> root;
private SBTNode<V> rightRotate(SBTNode<V> cur) {
SBTNode<V> leftNode = cur.l;
cur.l = leftNode.r;
leftNode.r = cur;
leftNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return leftNode;
}
private SBTNode<V> leftRotate(SBTNode<V> cur) {
SBTNode<V> rightNode = cur.r;
cur.r = rightNode.l;
rightNode.l = cur;
rightNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return rightNode;
}
private SBTNode<V> maintain(SBTNode<V> cur) {
if (cur == null) {
return null;
}
int leftSize = cur.l != null ? cur.l.size : 0;
int leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;
int leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
int rightSize = cur.r != null ? cur.r.size : 0;
int rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
int rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
if (leftLeftSize > rightSize) {
cur = rightRotate(cur);
cur.r = maintain(cur.r);
cur = maintain(cur);
} else if (leftRightSize > rightSize) {
cur.l = leftRotate(cur.l);
cur = rightRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
} else if (rightRightSize > leftSize) {
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur = maintain(cur);
} else if (rightLeftSize > leftSize) {
cur.r = rightRotate(cur.r);
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
}
return cur;
}
//root这棵树上的index位置添加节点cur,这个cur一定不是重复的,因为封装了一层,有不同的内存地址
private SBTNode<V> add(SBTNode<V> root, int index, SBTNode<V> cur) {
if (root == null) {
return cur;
}
//以root为根的树上的节点个数加1,可以理解为与之前“区间和个数”问题中的all数据项合并了
root.size++;
//左树及根节点一共有多少个节点
int leftAndHeadSize = (root.l != null ? root.l.size : 0) + 1;
if (index < leftAndHeadSize) {
root.l = add(root.l, index, cur);
} else {
root.r = add(root.r, index - leftAndHeadSize, cur); //在右树上位于自然时序的第几位
}
root = maintain(root);
return root;
}
private SBTNode<V> remove(SBTNode<V> root, int index) {
//找到要删除的节点过程中的沿途节点的size都要减1
root.size--;
int rootIndex = root.l != null ? root.l.size : 0;
if (index != rootIndex) {
if (index < rootIndex) {
root.l = remove(root.l, index);
} else {
root.r = remove(root.r, index - rootIndex - 1);
}
return root;
}
if (root.l == null && root.r == null) {
return null;
}
if (root.l == null) {
return root.r;
}
if (root.r == null) {
return root.l;
}
SBTNode<V> pre = null;
SBTNode<V> suc = root.r;
suc.size--;
while (suc.l != null) {
pre = suc;
suc = suc.l;
suc.size--;
}
if (pre != null) {
pre.l = suc.r;
suc.r = root.r;
}
suc.l = root.l;
suc.size = suc.l.size + (suc.r == null ? 0 : suc.r.size) + 1;
return suc;
}
private SBTNode<V> get(SBTNode<V> root, int index) {
int leftSize = root.l != null ? root.l.size : 0;
if (index < leftSize) {
return get(root.l, index);
} else if (index == leftSize) {
return root;
} else {
return get(root.r, index - leftSize - 1);
}
}
//add方法:在index位置加入num
public void add(int index, V num) {
SBTNode<V> cur = new SBTNode<V>(num); //先封装一层,以区分相同的num
if (root == null) {
root = cur;
} else {
if (index <= root.size) {
root = add(root, index, cur);
}
}
}
public V get(int index) {
SBTNode<V> ans = get(root, index);
return ans.value;
}
public void remove(int index) {
if (index >= 0 && size() > index) {
root = remove(root, index);
}
}
public int size() {
return root == null ? 0 : root.size;
}
}
// 通过以下这个测试,
// 可以很明显的看到LinkedList的插入、删除、get效率不如SbtList
// LinkedList需要找到index所在的位置之后才能插入或者读取,时间复杂度O(N)
// SbtList是平衡搜索二叉树,所以插入或者读取时间复杂度都是O(logN)
public static void main(String[] args) {
// 功能测试
int test = 50000;
int max = 1000000;
boolean pass = true;
ArrayList<Integer> list = new ArrayList<>();
SbtList<Integer> sbtList = new SbtList<>();
for (int i = 0; i < test; i++) {
if (list.size() != sbtList.size()) {
pass = false;
break;
}
if (list.size() > 1 && Math.random() < 0.5) {
int removeIndex = (int) (Math.random() * list.size());
list.remove(removeIndex);
sbtList.remove(removeIndex);
} else {
int randomIndex = (int) (Math.random() * (list.size() + 1));
int randomValue = (int) (Math.random() * (max + 1));
list.add(randomIndex, randomValue);
sbtList.add(randomIndex, randomValue);
}
}
for (int i = 0; i < list.size(); i++) {
if (!list.get(i).equals(sbtList.get(i))) {
pass = false;
break;
}
}
System.out.println("功能测试是否通过 : " + pass);
// 性能测试
test = 500000;
list = new ArrayList<>();
sbtList = new SbtList<>();
long start = 0;
long end = 0;
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * (list.size() + 1));
int randomValue = (int) (Math.random() * (max + 1));
list.add(randomIndex, randomValue);
}
end = System.currentTimeMillis();
System.out.println("ArrayList插入总时长(毫秒) : " + (end - start));
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * (i + 1));
list.get(randomIndex);
}
end = System.currentTimeMillis();
System.out.println("ArrayList读取总时长(毫秒) : " + (end - start));
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * list.size());
list.remove(randomIndex);
}
end = System.currentTimeMillis();
System.out.println("ArrayList删除总时长(毫秒) : " + (end - start));
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * (sbtList.size() + 1));
int randomValue = (int) (Math.random() * (max + 1));
sbtList.add(randomIndex, randomValue);
}
end = System.currentTimeMillis();
System.out.println("SbtList插入总时长(毫秒) : " + (end - start));
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * (i + 1));
sbtList.get(randomIndex);
}
end = System.currentTimeMillis();
System.out.println("SbtList读取总时长(毫秒) : " + (end - start));
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * sbtList.size());
sbtList.remove(randomIndex);
}
end = System.currentTimeMillis();
System.out.println("SbtList删除总时长(毫秒) : " + (end - start));
}
}