2022省赛

问题描述

对于一个长度为 N 的整数数列 ​, 小蓝想知道下标 l 到 r 的部 分和是多少?

然而, 小蓝并不知道数列中每个数的值是多少, 他只知道它的 M 个部分和 的值。其中第 i 个部分和是下标 ​ 到  的部分和 , 值是   。

输入格式

第一行包含 3 个整数 N、M 和 Q 。分别代表数组长度、已知的部分和数量和询问的部分和数量。

接下来 M 行, 每行包含 3 个整数  。

接下来 Q 行, 每行包含 2 个整数 l 和 r, 代表一个小蓝想知道的部分和。

输出格式

对于每个询问, 输出一行包含一个整数表示答案。如果答案无法确定, 输出 UNKNOWN。

样例输入

5 3 3
1 5 15
4 5 9
2 3 5
1 5
1 3
1 2

样例输出

15
6
UNKNOWN

【题目大意】 

对于一个序列，给出若干个局部区间和
再询问是否可以通过上述区间和计算出指定[L,R]的区间和

【思路】

求区间和，很容易联想到前缀和[L,R]的区间和：s[R] - s[L-1]
情景:
若已知[2,4],[5,7]的区间和，那么[2,7]的区间和就可以计算出来
区间[2,7]相当于把[2,4]和[5,7]合并了起来
可以通过并查集实现区间的合并，合并后整个大区间内的任意两个下标之间一定可以计算出区间和

解题关键:带权并查集

• 我们把序列的每个元素的下标当成一个节点，每给出一对已知的区间和[L,R],我们就把下标L-1和R合并到一个集合中
• 合并集合的过程中，除了L-1,R两个端点，我们还需要记录区间和，可以额外建立一个保存权值的列表，使用带权并查集维护。
• 此题的权值d[ ]，d[x]表示x和祖宗节点fx的距离，值为x-fx

知识补充：加权并查集
由于此题中，两个点维护集合时存在差值关系，因此使用并查集时，需要额外维护权值。

假设：d[ ]权值数组，d[x]表示x到父节点的权值，经过路径压缩后，d[x]应表示为x到祖宗节点的权值

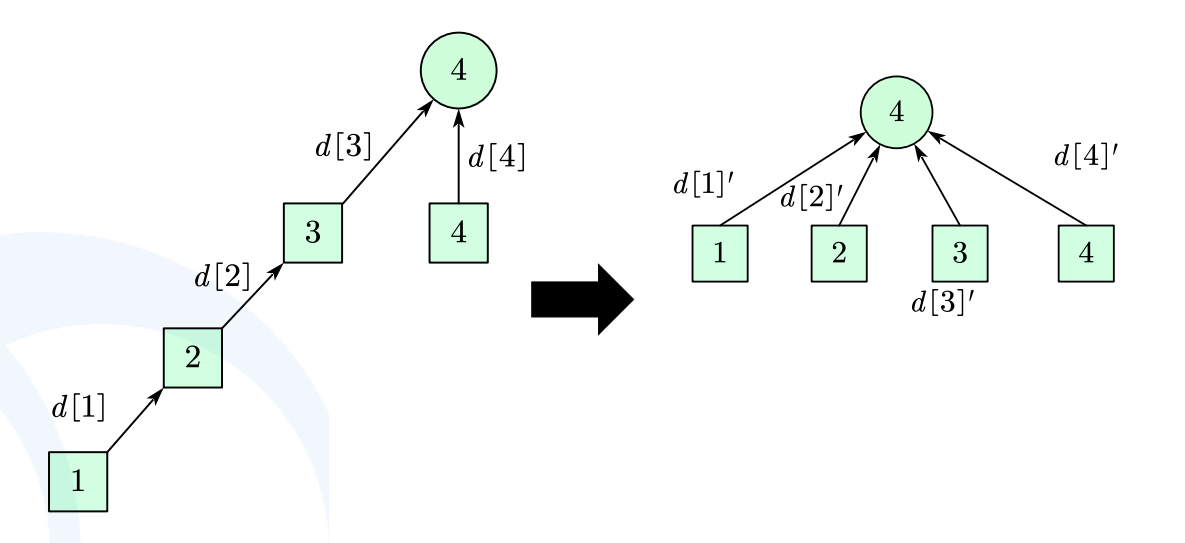
加权并查集的路径压缩

路径压缩后的权值变化
d[1]' = d[1]+d[2]＋d[3]

d[2]' = d[2]+d[3]
d[3]' = d[3]
d[4]' = d[4] 

举例：对样例进行加权并查集的路径压缩

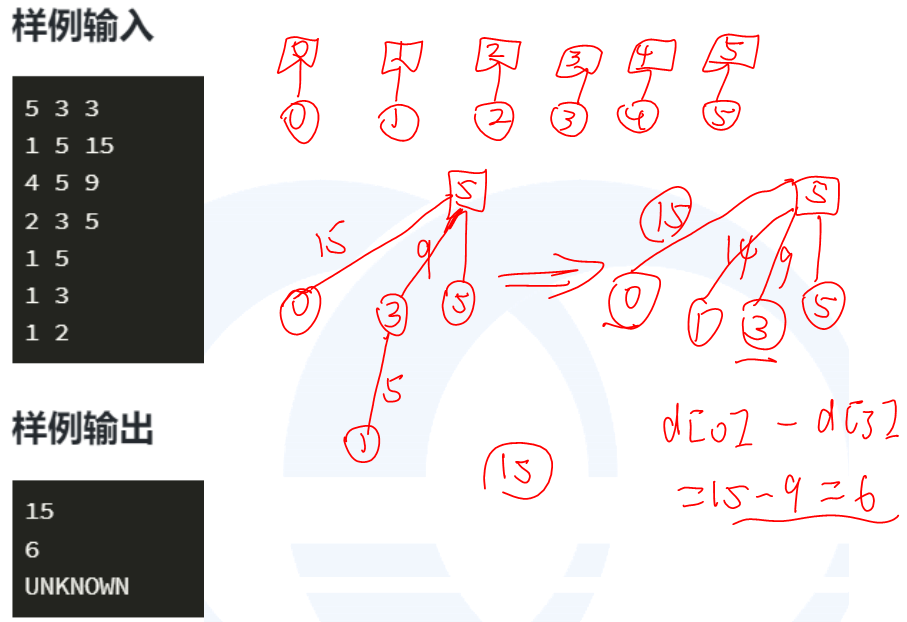
 带权值的路径压缩代码模板

def get_father(x :int):    #并查集组合的合并
    if x != father[x]:
        t = father[x]      #带权值的路径压缩，需要先记下father
        father[x] = get_father( father[x])
        d[x] += d[t]
    return father[x]

权值除了在路径压缩时需要更新外，在合并集合时，也需要更新

合并(x,y,s)时:    （注：s为[x,y]的区间和）
若fx,fy是x,y的祖宗节点，则合并fx,fy（将fx合并到fy）时d[fx] =s +d[y] - d[x]

 为什么是d[fx] =s +d[y] - d[x]？下面解释一下：

​​​d[x] = x - fx

d[y] = y - fy

所以：d[fx] = fx - fy = x- d[x] - (y - d[y]) = d[y] - d[x] + (x-y) = d[y] - d[x] + s

• 使用加权并查集，对于每对已知的左端点L，右端点R，和s，将L-1和R合并，合并过程中更新权值
• 所有已知区间和的合并操作完成后，对于接下来的每个查询[L1,R1]区间和，判断L1-1，R1是否属于同一集合，如果是，那么d[L1-1]-d[R]即为[L1,R1]的区间和，如果不是，说明此时的区间和无法求解。

 【代码】

N, M, Q = map(int, input().split())
father = [0] * (N + 10)
d = [0] * (N + 10)
def init(n):
    for i in range(1, n + 1):
        father[i] = i
def find_father(x):
    if x != father[x]:
        t = father[x]  # 带权值的路径压缩，需要先记下father
        father[x] = find_father(father[x])
        d[x] += d[t]   # 累加上一层的权值
    return father[x]

init(N)
for i in range(M):
    l, r, w = map(int, input().split())
    fl, fr = find_father(l - 1), find_father(r)  # 找出父节点
    if fl != fr:            # 不是在一个集合
        father[fl] = fr     # 将fr加入fl集合
        d[fl] = d[r] - d[l - 1] + w

ans = []
for i in range(Q):
    l, r = map(int, input().split())
    fl, fr = find_father(l - 1), find_father(r)
    if fl != fr:
        # print("UNKNOWN")
        ans.append("UNKNOWN")
    else:
        # print(d[l - 1] - d[r])
        ans.append(d[l - 1] - d[r])

for i in ans:
    print(i)