实验一 基于MATLAB语言的线性离散系统的Z变换分析法

一、实验目的

1. 学习并掌握 Matlab 语言离散时间系统模型建立方法；

2．学习离散传递函数的留数分析与编程实现的方法；

3．学习并掌握脉冲和阶跃响应的编程方法；

4．理解与分析离散传递函数不同极点的时间响应特点。

二、实验工具

1. MATLAB 软件（6.5 以上版本）；

2. 每人计算机一台。

三、实验内容

1. 在Matlab语言平台上，通过给定的离散时间系统差分方程，理解课程中Z变换定义，掌握信号与线性系统模型之间Z传递函数的几种形式表示方法；

2. 学习语言编程中的Z变换传递函数如何计算与显示相应的离散点序列的操作与实现的方法，深刻理解课程中Z变换的逆变换；

3. 通过编程，掌握传递函数的极点与留数的计算方法，加深理解G（z）/z 的分式方法实现过程；

4. 通过系统的脉冲响应编程实现，理解输出响应的离散点序列的本质，即逆变换的实现过程；

5. 通过编程分析，理解系统的Z传递函数等于单位脉冲响应的Z变换，并完成响应的脉冲离散序列点的计算；

6. 通过程序设计，理解课程中脉冲传递函数极点对系统动态行为的影响，如单独极点、复极点对响应的影响。

四、实验步骤

1.创建系统

%How to create digital system g % Four examples are as follows:

numg=[0.1 0.03 -0.07];  

deng=[1 -2.7 2.42 -0.72]; 

g=tf(numg,deng,-1)  

get(g);

[nn dd]=tfdata(g,'v')   

[zz,pp,kk]=zpkdata(g,'v')  

%Unite circle region with distrbuting zeros points and poles points

hold on

pzmap(g), hold off  

axis equal

运行结果：

 

 

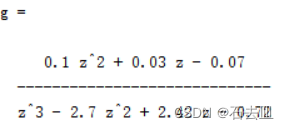
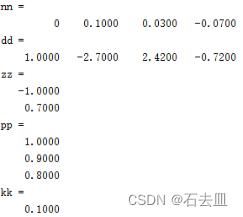
2.转换为零极点标准形式

    %Convert from tf(z-function) to zpk(z-function) %Part C exercise form

gg=zpk(g)

[zz,pp,kk tts]=zpkdata(gg,'v')

[z,p k,ts]=zpkdata(g,'v')            

运行结果：

 

1. 四个例子

% Four examples are as follows:

% Part A exercise

eg1mun=[1.25 -1.25,0.30];

eg1den=[1 -1.05 0.80 -0.10];

eg1=tf(eg1mun,eg1den,-1);

eg1zpk=zpk(eg1);

[zz1,pp1,kk1,tts1]=zpkdata(eg1zpk,'v');

%Part B exercise

eg2mun=[0.84 -0.062 -0.156 0.058];

eg2den=[1 -1.03 0.22 0.094 0.05];

eg2=tf(eg2mun,eg2den,-1);

eg2zpk=zpk(eg2);

[zz2,pp2,kk2,tts2]=zpkdata(eg2zpk,'v');

%Part C exercise

zz3=[-0.2 0.4];

pp3=[0.6 0.5+0.75i 0.5-0.75i 0.3];

kk3=150;

tts3=-1;

eg3zpk=zpk(zz3,pp3,kk3,tts3);

eg3=tf(eg3zpk);

%Part D exercise

zz4=[-0.3 0.4+0.2i 0.4-0.2i];

pp4=[-0.6 -0.3,0.5 0.6];

kk4=5;

tts4=-1;

eg4zpk=zpk(zz4,pp4,kk4,tts4);

eg4=tf(eg4zpk);

1. 留数法

% Residue method and impluse response

numg=[2 -2.2 0.65];

deng=[1 -0.6728 0.0463 0.4860];

[rGoz, pGoz,other]=residue(numg,[deng 0])

%[mag_pGoz,theta_pGoz] =xy2p(pGoz)

%[mag-rGoz,theta-rGoz]=xy2p(rGoz)

G=tf(numg,deng,-1)

impulse(G)

[y,k]=impulse(G);

stem(k,y,'filled');

impulse(G)

运行结果：

 

1. 复杂极点响应

%When transfer function is G(Z) with complex ,t=t*ts;pole of z=e^(+-j*30*pi/3) and z=-0.5,as well as its gain value is unit step signal,its collecting cycle is 0.5 second,how to analyze its response.

gcf

ts=0.3;

num=[1 0.5];

den=conv([1 -exp(i*pi/3)],[1 -exp(-i*pi/3)]);

g1=tf(num,den,ts)

[y,k]=impulse(g1,20);

stem(k,y,'filled'),grid

运行结果：

 

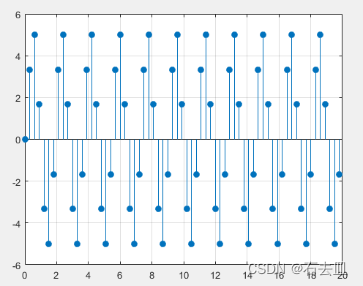
1. 重极点响应

% How to analyze response with repeating poles dtime=[0:90];

%y(k+2)-1.8y(k+1)+0.81y(k)=3u(k+1)-1.2u(k) yi=impulse(gstep,dtime)

gcf

num=[3 -1.2];

den=[1 -1.8 0.81];

[rGoz, pGoz,other]=residue(num,[den 0])

t=0:60;

y=rGoz(2,1).*(t.*(pGoz(2,1).^(t-1)))+rGoz(1,1).*(pGoz(1,1).^(t))

y1=zeros(1,61);

y1(1,1)=rGoz(3,1);

y=y+y1;

t=ts*t;

stem(t,y,'filled'),grid

%Special example about difference real pole to

system response

%[rGoz,pGoz,other]=residue(num,[den,0])

%num1=[rGoz(1) 0];

%den1=[1 -pGoz(1)]

%gg1=tf(num1,den1,ts)

%[y,t]=impulse(gg1,50)

%stem(t,y,'filled'),grid

运行结果：

 

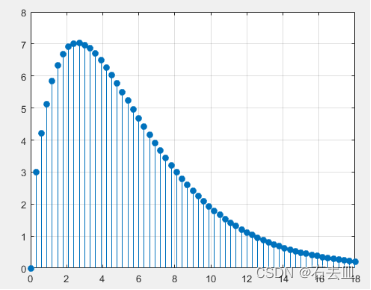
1. 阶跃响应

numg=[2 -2.2 0.56];

deng=[1 -0.6728 0.0463 0.4860];

g=tf(numg,deng,1);

numgstep=[numg 0];

dengstep=conv(deng,[1 -1]);

gstep=tf(numgstep,dengstep,1)

dtime=[0:90];

yi=impulse(gstep,dtime)

subplot(2,1,1)

stem(dtime,yi,'filled')

ys=step(g,dtime);

subplot(2,1,2)

stem(dtime,ys,'filled')

dcgain(g)

ys_ss=ys(end)

ys_ss=ys(max(dtime))

运行结果：

 

 

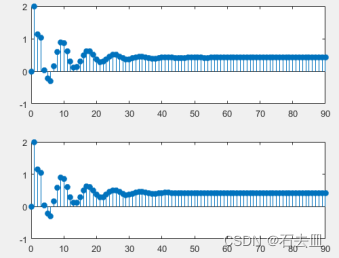
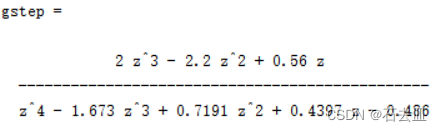
% Example 1: Analysis of subsection input function

subplot(1,1,1)

num=[2 -2.2 0.56];

den=[1 -0.6728 0.0463 0.4860];

ts=0.2;

g=tf(num,den,ts);

dtime=[0:ts:8]';

u=2.0*ones(size(dtime));

ii=find(dtime>=2.0); u(ii)=0.5;

y=lsim(g,u,dtime);

stem(dtime,y,'filled'),grid

hold on

plot(dtime,u,'o')

hold off

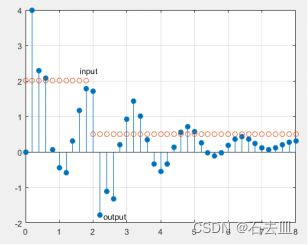
text(2.3,-1.8,'output')

text(1.6,2.3,'input')

运行结果：

 

• 实验思考

1、根据实验结果，分析离散传递函数不同极点的时间响应特点。

离散系统的时间响应是由各个极点时间响应的线性叠加而成的，根据极点在不同的位置我们可以看出如下规律：

1. 极点在单位圆外的正实轴上，对应的暂态响应分量单调发散；
2. 极点在单位圆与正实轴的交点，对应的暂态响应分量是等幅的；
3. 极点在单位圆内的正实轴上，对应的暂态响应分量单调衰减；
4. 极点在单位圆内的负实轴上，对应的暂态响应分量是以2T为周期正负交替的衰减振荡；
5. 极点在单位圆与负实轴的交点，对应的暂态响应分量是以2T为周期正负交替的等幅振荡；
6. 极点在单位圆外的负实轴上，对应的暂态响应分量是以2T为周期正负交替的发散振荡。

1. 通过程序设计，分析不同的传递函数极点 如单独极点、复极点、重根极点对系统动态行为的影响

   当极点是稳定的单极点时，系统的输出如图所示：

 

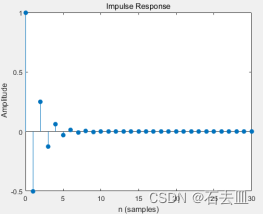
 当极点是稳定的实极点时，系统的输出如图所示：

 

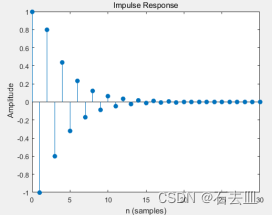
 当极点是稳定复极点时，系统的输出如图所示：

 

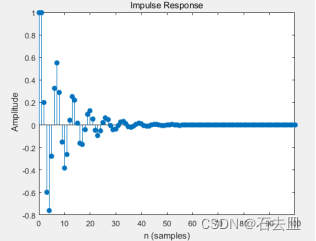
 当极点是稳定重实极点时，系统的输出如图所示：

 

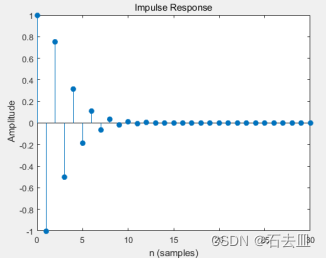
1. 分析留数法的意义，根据系统的阶跃响应判别系统稳定性

留数法相对于长除法以及部分分式法，得出的结果更加准确，可以直观看出z变换的形式，无论是有理形式还是非有理形式均可以运用，因此留数法更加实用。当系统是稳定无差系统时，系统的阶跃响应与输入理想情况相等，当系统是有差稳定系统时，阶跃响应会存在一定偏差，如果是不稳定系统，系统输出将会发散。

1. 对 Z 变换的进一步思考。

    从z变换的本质来看，实际上就是对离散信号和系统的拉普拉斯变换，由此我们会根本容易理解Z变换的重要性，同时也可以看出Z变换和傅里叶变换之间的关系。Z变换中的Z平面与拉普拉斯中的S平面存在映射的关系，即z=exp(Ts)。在Z变换中，单位圆上的结果即对应离散时间傅里叶变换的结果。因此，Z变换也是一种非常重要的分析工具。