目录
- 一、回顾
- 二、图嵌入概述
- 2.1 补充知识——表示学习
- 2.2 图嵌入
- 2.3 图嵌入-基本框架 编码器——解码器
- 2.3.1 编码器
- 2.3.2 解码器
- 2.3.3 执行步骤
- 2.4 随机游走
- 2.4.1 随机游走的方法步骤
- 2.4.2 计算优化
- 三、随机梯度下降
- 3.1 SGD步骤
- 3.2 批处理
- 四、node2vec
- 五、基于随机游走的图嵌入的缺点:
- 六、deepwalk优缺点
- 参考文献
一、回顾
本门课程主线是将图转化为连续稠密的向量,本文及之前的文章均为不讲属性特征,只讲社群连接特征。
如何将节点转化为D维向量
- 人工特征学习:节点重要度,集群系数,Graphlet
- 图表式学习:通过随机游走构造自监督学习网络。DeepWalk,Node2Vec
- 矩阵分解
- 深度学习:图神经网络
本文主要讲的是图嵌入(Graph Embedding)
由节点,边,子图,全图,基于手工构造特征,矩阵分解,随机游走,图神经网络
二、图嵌入概述
2.1 补充知识——表示学习
表示学习:自动学习特征。将各模态输入转为向量
2.2 图嵌入
只利用节点连接信息,没有节点属性信息
将节点映射为d维向量
低维:向量维度远小于节点数
连续:每个元素都是实数(有正有负,有大有小)
稠密:每个元素都不为0

2.3 图嵌入-基本框架 编码器——解码器
2.3.1 编码器
- 实现功能:输入一个节点,输出这个节点对应的D维向量
- 最简单的编码器:查表(将所有节点的相关度直接写为一张表) E N C ( v ) = z v = Z ⋅ v ENC(v)=z_v=Z\cdot v ENC(v)=zv=Z⋅v
- Z表示一个矩阵,每一列表示一个节点,行数表示向量的维度
- 优化Z矩阵的方法:DeepWalk、Node2Vec
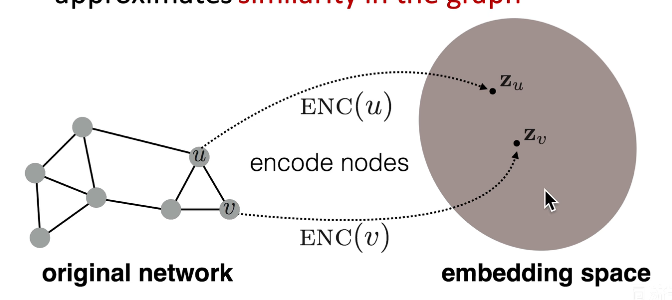
2.3.2 解码器
-
实现功能:输入需人为定义的节点相似度,输出向量点乘数值(余弦相似度)。
s i m i l a r i t y ( u , v ) ≈ z v T z u {similarity(u,v)\approx z_v^Tz_u} similarity(u,v)≈zvTzu
e.g若定义两节点相连即位相似,则 i f if if两节点之间相连,则向量点乘数值会接近1; e l s e else else节点不相连,则节点向量会接近垂直,向量点乘数值会接近0.
-
直接优化嵌入向量,使用随机游走方式,如果两个节点出现在同一个随机游走序列中,就反映了这两个节点是相似的,并与下游任务无关
2.3.3 执行步骤
- 编码器:节点->D维向量。
- 定义一个节点相似度函数。
- 解码器DEC地图从嵌入到相似度评分。
- 迭代优化每个节点的D维向量,使得图中相似节点向量数量积大,不相似节点向量数量积小。
2.4 随机游走
-
定义:随机游走(英语:Random Walk,缩写为 RW),是一种数学统计模型,它是一连串的轨迹所组成,其中每一次都是随机的。
-
可以与NLP一一对应

2.4.1 随机游走的方法步骤
- P ( v ∣ z u ) P(v∣z_u) P(v∣zu):从 u u u节点触发的随机游走序列经过 v v v节点的概率
- 使用softmax方法计算 P ( v ∣ z u ) P(v∣z_u) P(v∣zu): σ ( z ) [ i ] = e z [ i ] ∑ j − 1 K e z [ j ] σ(z)[i]=\frac{e^{z[i]}}{∑^K_{j-1}e^{z[j]}} σ(z)[i]=∑j−1Kez[j]ez[i]
- 具体步骤:
- 采样得到若干随机游走序列,计算条件概率 P ( v ∣ z u ) P(v∣z_u) P(v∣zu)
- 迭代优化每个节点的D维,使得序列中共现节点向量数量积大,不共现节点向量数量积小,计算结果反映了向量相似度
- 优点:表示能力、计算便捷、无监督/自监督学习问题(没用到任何标签)
- 使用极大似然估计,优化目标函数 m a x f ∑ u ∈ V l o g P ( N R ( u ) ∣ z u ) \underset{f}{max}\mathop{\sum}\limits_{u\in V}logP(N_R(u)|z_u) fmaxu∈V∑logP(NR(u)∣zu)其中 N R ( u ) N_R(u) NR(u)表示从u节点出发的随机游走序列的所有邻域节点
- 整个优化的目标函数:
 其中
其中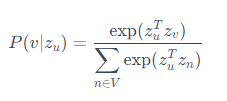 遍历所有节点,并遍历从u节点出发的随机游走序列的所有邻域节点,计算节点u和节点v在该随机游走序列中共现。
遍历所有节点,并遍历从u节点出发的随机游走序列的所有邻域节点,计算节点u和节点v在该随机游走序列中共现。
2.4.2 计算优化
1.负采样
l o g ( e x p ( z u T z v ) ∑ n ∈ V e x p ( z u T z n ) ) ≈ l o g ( σ ( z u T z v ) ) − ∑ i = 1 k l o g ( σ ( z u T z n i ) ) , n i P v ( 非均匀分布采样 ) log(\frac{exp(z_u^Tz_v)}{\mathop{\sum}\limits_{n\in V}exp(z_u^Tz_{n})})\approx log(\sigma(z_u^Tz_{v}))-\mathop{\sum}\limits_{i=1}^{k}log(\sigma(z_u^Tz_{ni})),n_i ~P_v(非均匀分布采样) log(n∈V∑exp(zuTzn)exp(zuTzv))≈log(σ(zuTzv))−i=1∑klog(σ(zuTzni)),ni Pv(非均匀分布采样)
2.k的选择,最好在5~20之间
3.理论上同一个随机游走序列中的节点不应当被用为负样本,但是在图神经网络中,图的样本足够大,使得很难重复,因此使用同一图
三、随机梯度下降
3.1 SGD步骤
- 采样,生成Mini-batch
- 前向推断,或损失函数
- 反向传播,求每个权重的更新速度
- 优化更新权重
3.2 批处理

四、node2vec
可设置深度优先还是广度优先
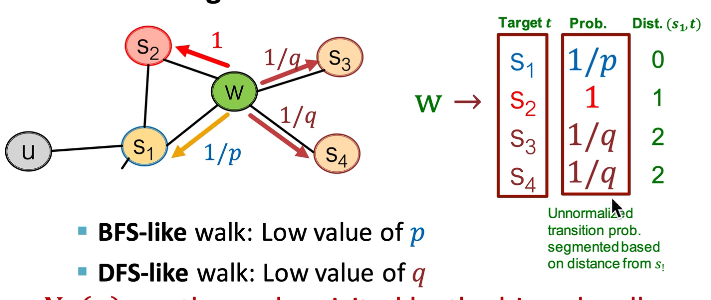
由两个参数p,q控制是上回还是去下一个节点

Node2Vec算法:
计算每条边的随机游走概率
以u节点为出发点,长度为l*,生成r*个随机游走序列
用随机梯度下降优化目标函数
五、基于随机游走的图嵌入的缺点:
- 随机游走的图嵌入方法都是对图中已有的节点计算特征,无法立刻泛化到新加入的节点,其实是某种程度的过拟合
- 只是探索相邻局部信息,只能采样出地理上相近的节点
- 仅利用图本身的连接信息,并没有使用属性信息
六、deepwalk优缺点

参考文献
[1] 斯坦福CS224W图机器学习、图神经网络、知识图谱【同济子豪兄】