动归算法专题
1.拆分词句

- 是不是,在不在都是可以用动归解决的
- 状态转义方程不一定都是等式,也有可能是条件
2.三角形

- 动归算法也不是一定要借助新开空间,也是可以用自己原来的空间
3.背包问题

4.分割回文串-ii

5.不同的子序列

贪心算法专题
- 只管一步的最优结果,
1.分割平衡字符串
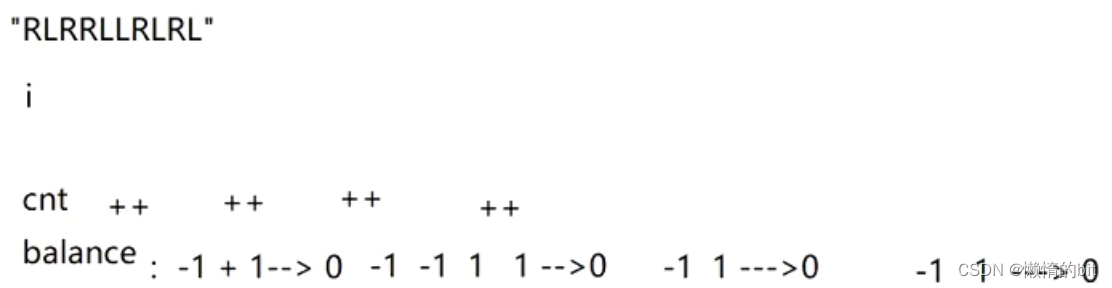
- 贪心策略: 不让平衡字符串嵌套
2.买卖股票的最佳时机
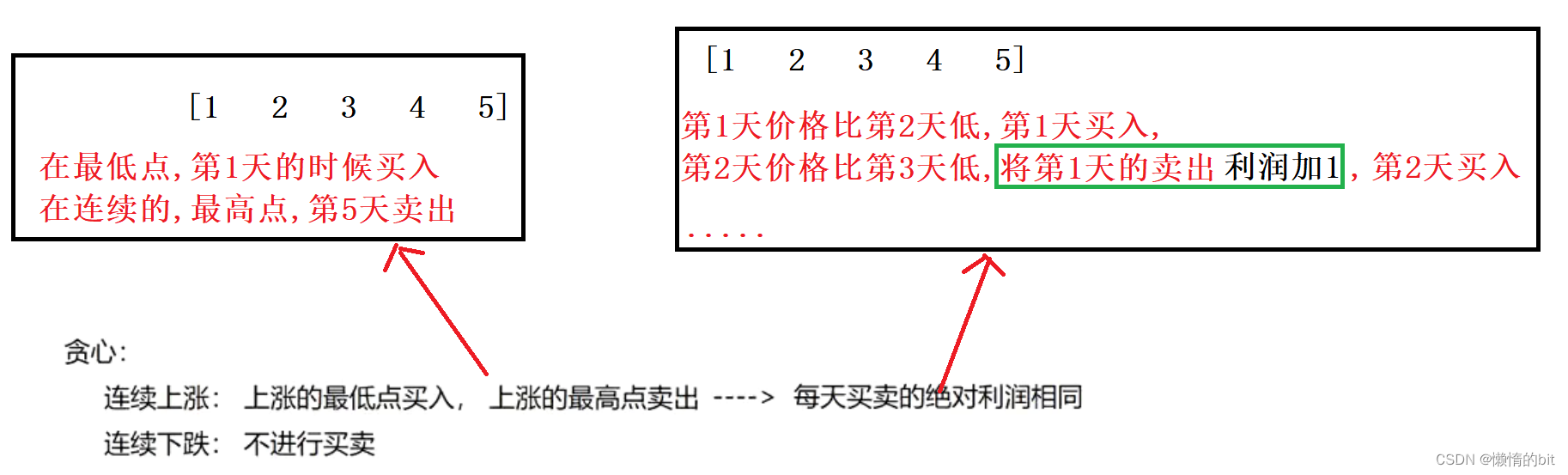
- 贪心策略:只要后一天的股票比前一天的股票高,
就把前一天的股票卖了,买后一天的股票
3. 跳跃游戏
- 贪心策略: 站在每一个位置,更新最远可以到达的位置
4.最多可以参加的会议数目

- 贪心策略: 每一天取结束时间最早的会议
回溯算法专题
深度优先遍历
1.员工的重要性
- 哈希 + 深度优先遍历(递归)
2.图像渲染
- 深度优先遍历(递归)
3.电话号码的字母组合
- 全排列 + 回溯
4.组合总和
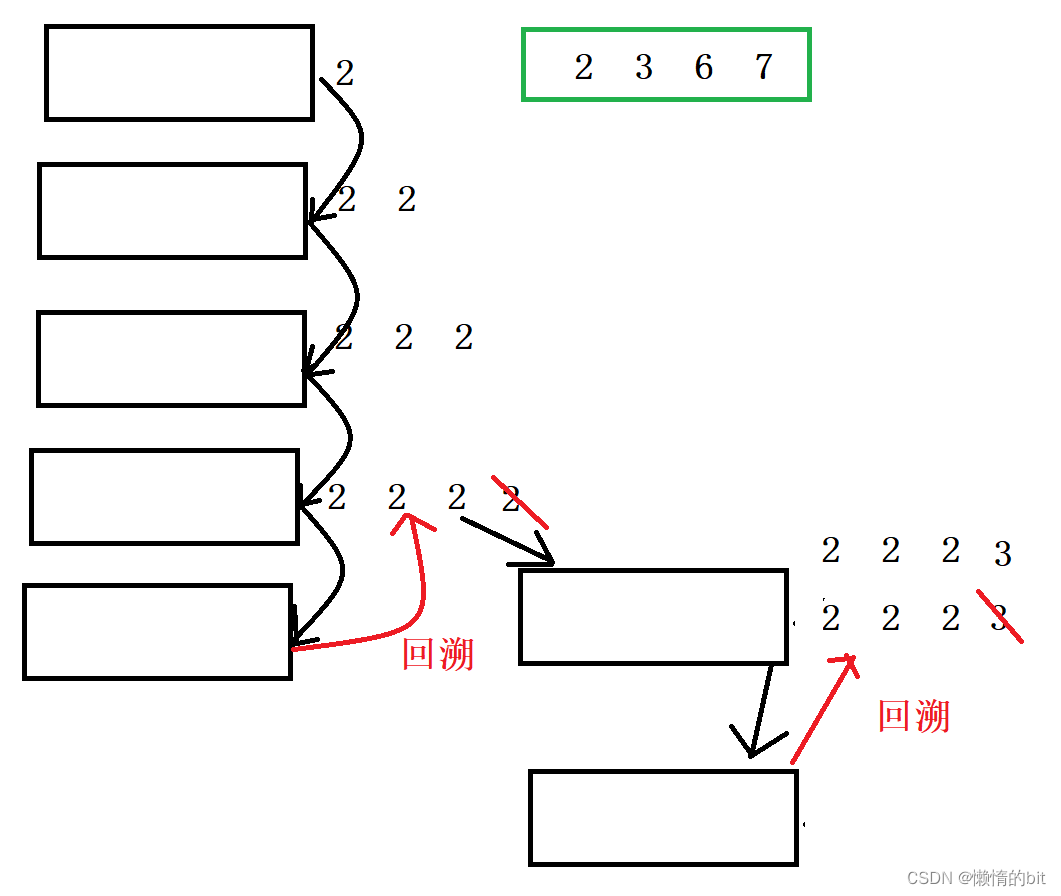
- 回溯一般在递归之后
5.N皇后
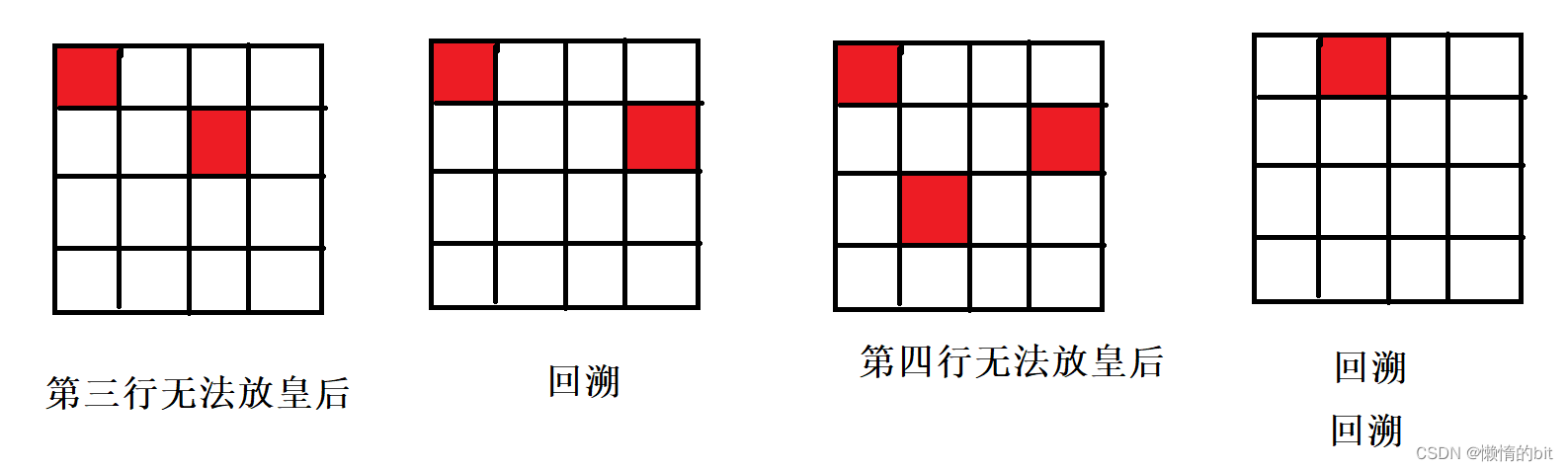
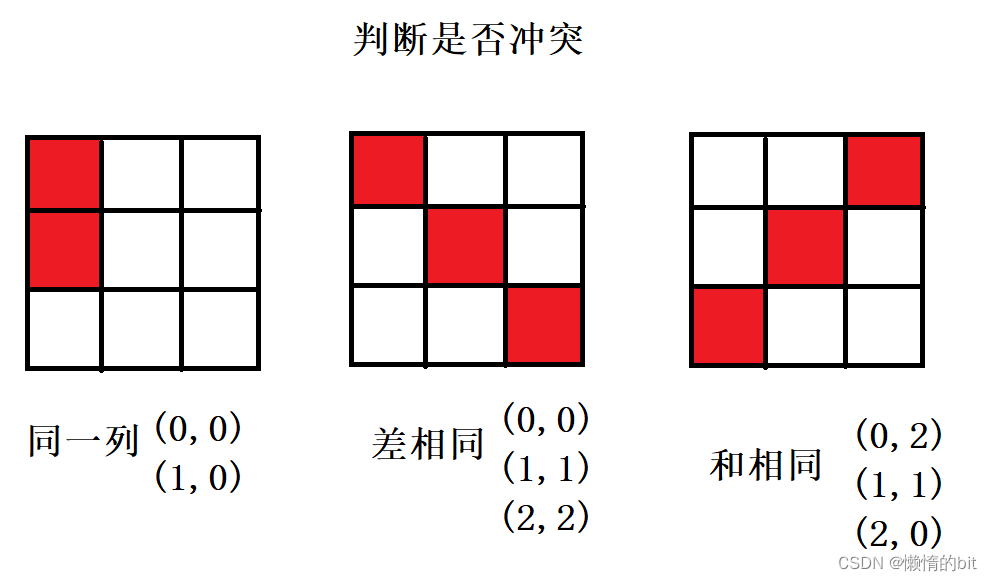
- 需要一个全部位置矩阵(存放全部为位置),需要一个临时矩阵(存放一个结果的位置矩阵)
- 遍历每列,需要一个判断是否冲突的函数,不冲突放入,DFS(下一行)+回溯
- 最后再把全部位置矩阵转换成字符串矩阵
广度优先遍历
1.腐烂的橘子
- 广度优先一般不用递归,多使用队列来实现层序遍历
2.单词接龙
- 从题目分析wordList中的单词只能使用一次,使用unordered_map<string,bool>u_s;
3.打开转盘锁
-
unordered_set<string>book;可能会出现重复的字符串,对已经搜索过的,不再搜索,
字符串匹配算法
BF算法

- BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配,
- 若相等,则继续比较S的第二个字符和 T的第二个字符;
- 若不相等,则比较S的第二个字符(i - j + 1)和 T的第一个字符(j = 0),依次比较下去,直到得出最后的匹配结果
#include <iostream>
#include <assert.h>
using namespace std;
int BF(const char* str, const char* sub)
{
assert(str != NULL && sub != NULL);
if (str == NULL || sub == NULL)
{
return -1;
}
int i = 0;
int j = 0;
int strLen = strlen(str);
int subLen = strlen(sub);
while (i < strLen && j < subLen)
{
if (str[i] == sub[j])
{
i++;
j++;
}
else
{
//回退
i = i - j + 1;
j = 0;
}
}
if (j >= subLen)
{
return i - j;
}
return -1;
}
int main()
{
printf("%d\n", BF("ababcabcdabcde", "abcd"));
printf("%d\n", BF("ababcabcdabcde", "abcde"));
printf("%d\n", BF("ababcabcdabcde", "abcdef"));
return 0;
} 
- 时间复杂度分析:最坏为O(m*n); m是主串长度,n是子串长度
KMP算法
-
KMP 算法是一种 改进 的 字符串匹配算法
-
KMP 和 BF 唯一不一样的地方在,我主串的 i 并不会回退,并且 j 也不会移动到 0 号位置
1. 首先举例,为什么主串不回退?

- 假设目前在2号位置匹配失败,就算回退到1位置,也是没有必要的,
- 1位置的字符b和字串0位置a,也不一样,
2.j的回退位置
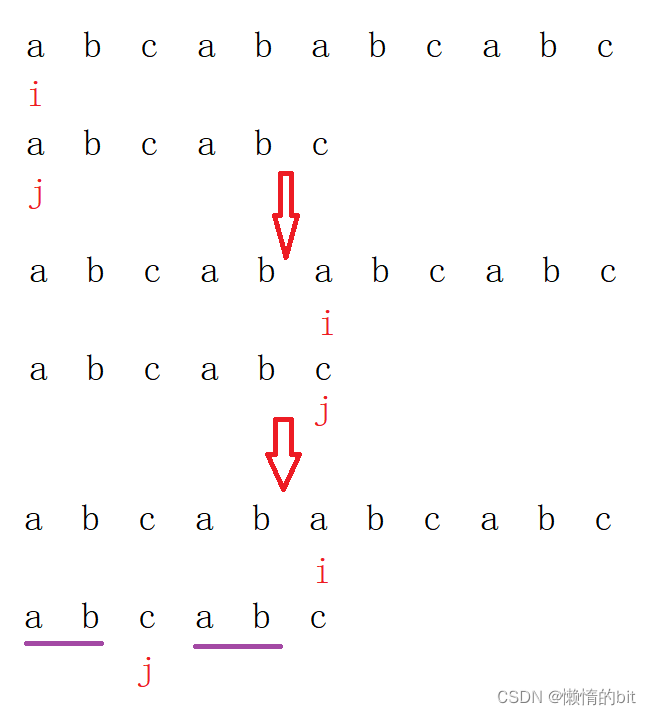
- 当匹配失败的时候,我们不进行回退i,
- 因为在这个地方匹配失败,说明i的前面和j的前面,必定有一部分是相同的,不然两个下标不可能走到这里来
- 从这个图中可以看出,如果j回退到2下标(字符c的位置),j不回退,这就是最好的情况了
通过上面的描述,kmp算法:就是匹配失败,i不变,j回退到一个最佳位置,
而想要得到这个最佳位置就需要引出next数组
next数组的引入

- next[j] = k;来表示,不同的j来对应一个 K 值, 这个 K就是你将来要移动的j要移动的位置。
- k值的求法: 找到匹配成功部分的两个相等的真子串(不包含本身),
- 一个以下标 0 字符开始,另一个以 j-1 下标字符结尾。
-
初始化: next[0] = -1;next[1] = 0
next数组的推导
情况一: 前提next[i] = k ,当p[i] == p[k]时
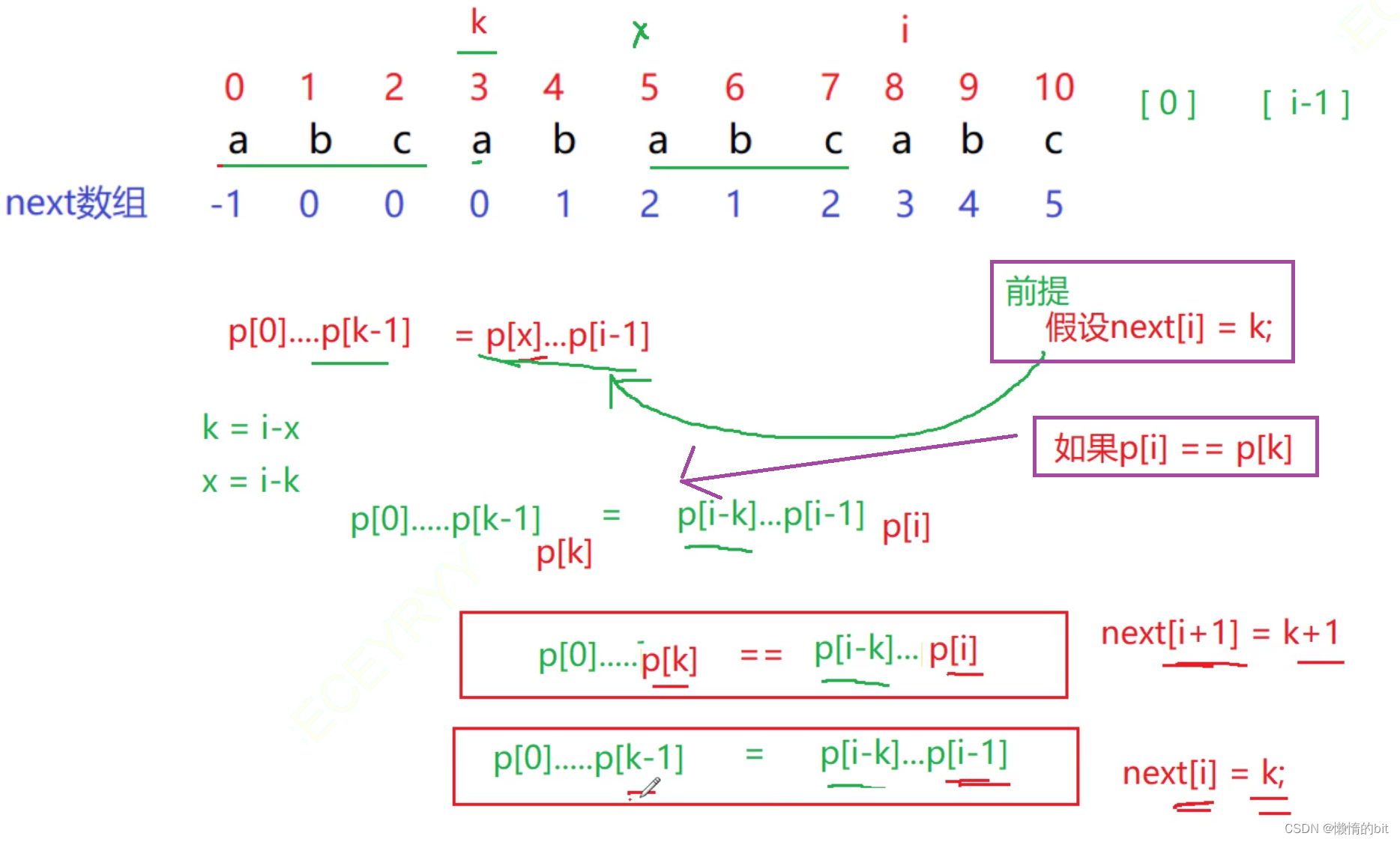
情况二: 前提next[i] = k ,当p[i] != p[k]时
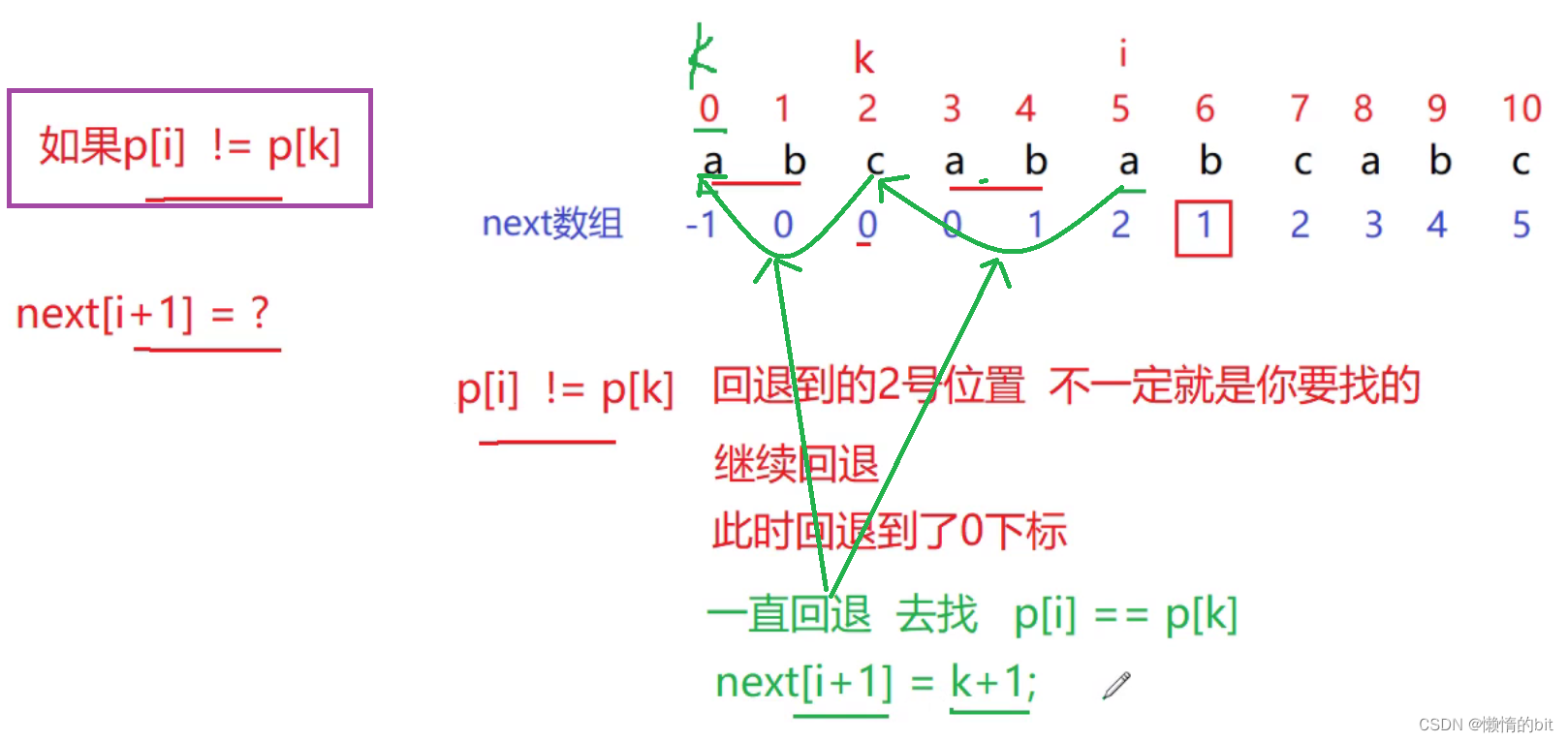
#include <iostream>
#include <assert.h>
#include <vector>
using namespace std;
vector<int> get_next(string& s) {
vector<int>next(s.size(), -1);
// 初始化
if (s.size() > 1) {
next[1] = 0;
}
int i = 2;// 从下标2开始
int k = 0;// 前一项的k值
while (i < s.size()) {
if (k == -1 || s[i - 1] == s[k]) {
next[i] = ++k;
i++;
}
else {
k = next[k];// 回退
}
}
return next;
}
int KMP(string& str, string& sub, int pos) {
if (str.empty() || sub.empty()) {
return -1;
}
if (sub.length() > str.length()) {
return -1;
}
assert(pos >= 0 && pos < str.length());
// string tmp = str;
vector<int> next = get_next(sub);
// 先默认pos等于0;
int i = pos;// 主串下标
int j = 0;// 字串下标
while (i < str.length() && j < sub.length()) {
if (j == -1 || str[i] == sub[j]) {
i++; j++;
}
else {
// i不变,j回退到一个最佳位置
j = next[j];
}
}
if (j >= sub.length()) {
return i - j ;// 下标
}
return -1;
}
int main()
{
string s1 = "abcababcabc";
string s2 = "abcabc";
int pos = KMP(s1, s2,0);
cout << pos << endl;
return 0;
}
对next数组的优化
vector<int> get_next(string& s) {
vector<int>next(s.size(), -1);
// 初始化
if (s.size() > 1) {
next[1] = 0;
}
int i = 2;// 从下标2开始
int k = 0;// 前一项的k值
while (i < s.size()) {
if (k == -1 || s[i - 1] == s[k]) {
next[i] = ++k;
if (s[next[i]] == s[i]) {
next[i] = next[next[i]];
//k = next[i];
}
i++;
}
else {
k = next[k];// 回退
}
}
return next;
}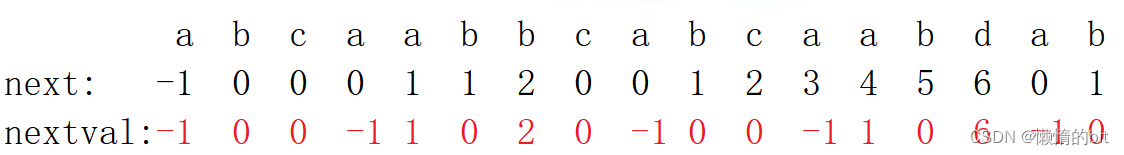
- nextval数组的求法很简单,如果当前回退的位置,正好是和当前字符一样,那么就写那个字符的nextval值,反之就不变