文章目录
- 约束优化:低维线性时间线性规划算法(Seidel算法)、低维线性时间严格凸二次规划算法
- 带约束优化问题的定义
- 带约束优化问题的分类及时间复杂度
- 低维线性规划问题
- 定义
- Seidel线性规划算法
- 低维严格凸二次规划问题
- 定义
- 低维情况下的精确最小范数算法:将Seidel的算法从LP推广到严格凸的QP上。
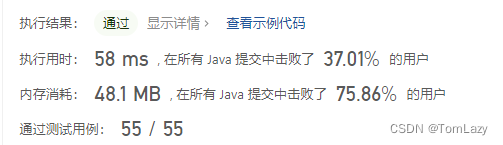
- c++代码
- 参考文献
约束优化:低维线性时间线性规划算法(Seidel算法)、低维线性时间严格凸二次规划算法
带约束优化问题的定义

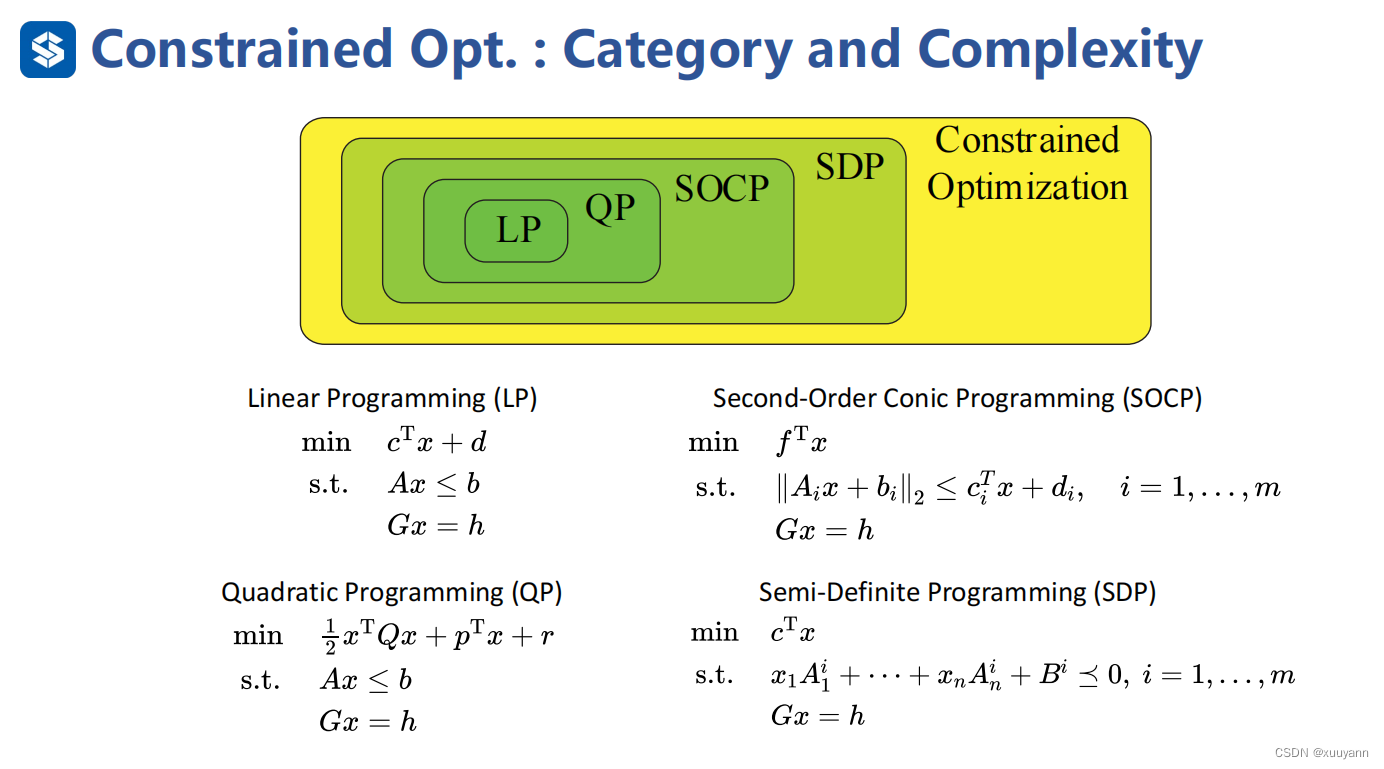
带约束优化问题的分类及时间复杂度
- 线性规划问题(LP)
- 二次规划问题(QP)
- 二次锥规划问题(SOCP)
- 半正定规划问题(SDP)

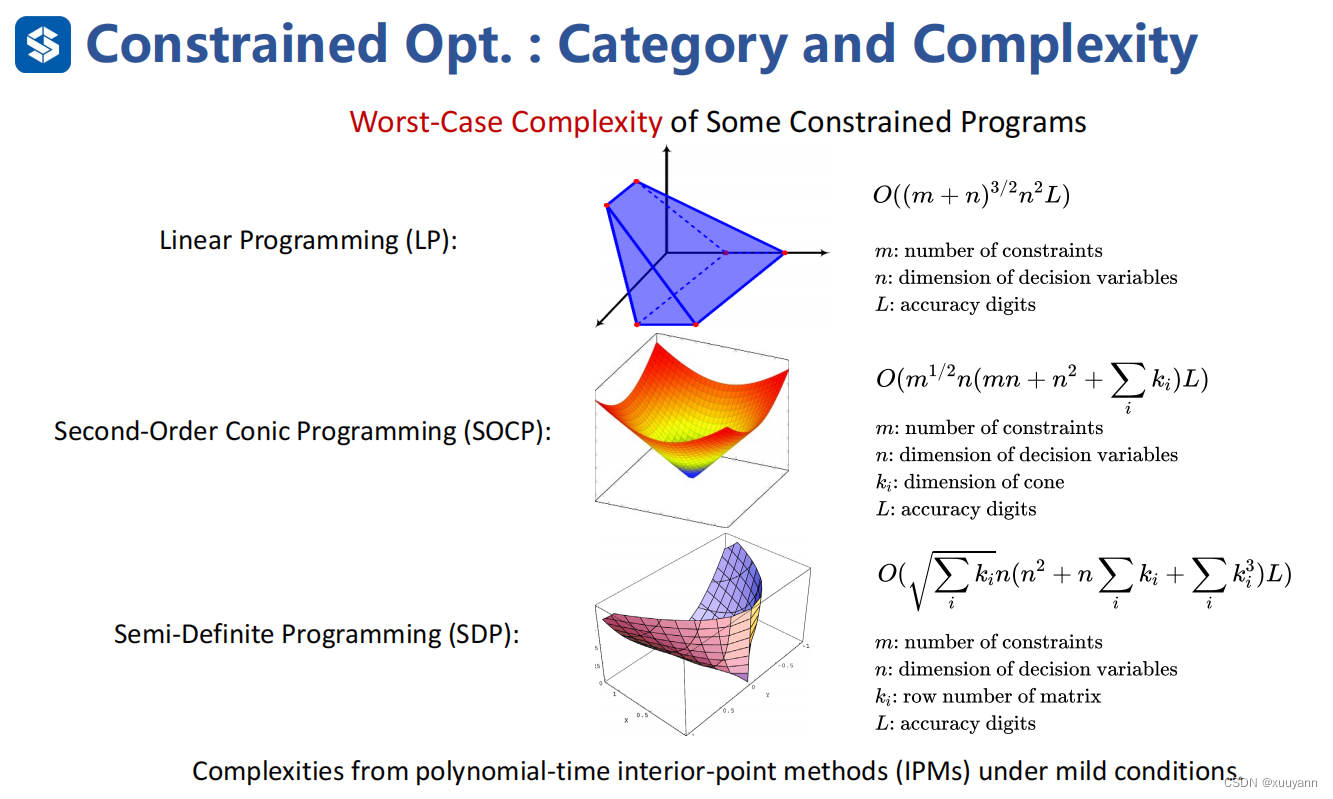
优化算法可以分为精确算法和非精确算法,顾名思义精确算法就是可以得到优化问题的精确解,非精确算法只能得到有一定保证的近似解。虽然前者可以通过有限次迭代得到精确解,但适用范围很窄,后者可适用于更多实际问题。
低维线性规划问题
定义
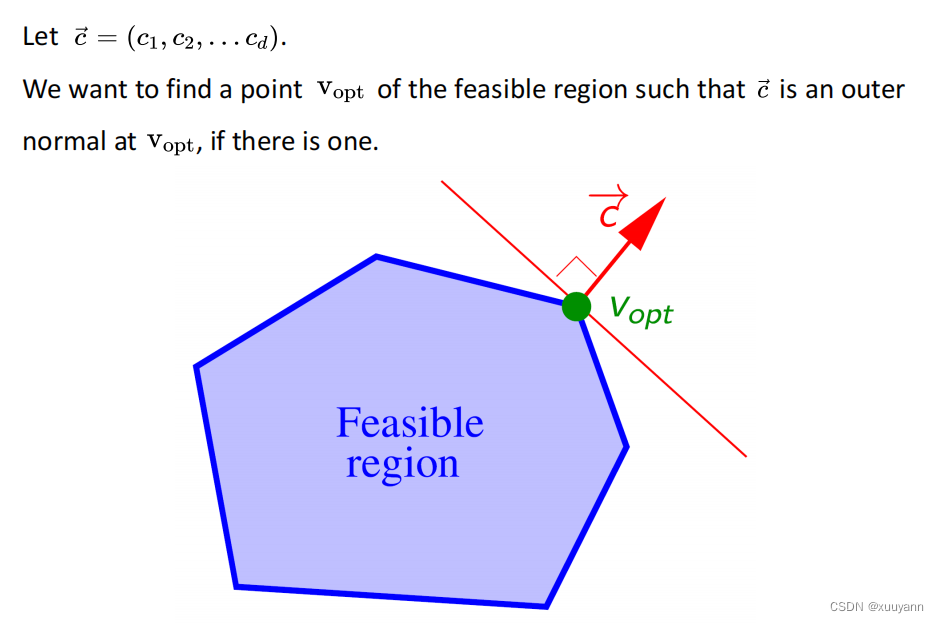
目标函数和约束函数均为线性的,低维线性规划问题的维度是优化变量的维度 d d d,一般很小,比如三维四维等,但约束的个数n可以很大很大。

线性规划问题的可行解集是约束半空间 ∈ R d \in \mathbb{R}^d ∈Rd的交集,是一个凸多面体几何 ∈ R d \in \mathbb{R}^d ∈Rd,最优解在可行解集边缘或者顶点处。如下图所示,对于目标函数 f ( x ) = c ⊤ x f(x)=c^{\top}x f(x)=c⊤x,构造一个以 c ⃗ \vec{c} c为法向量的平面,这个平面构成的半空间 c ⊤ ( x − V o p t ) ⩽ 0 c^{\top}(x-V_{opt}) \leqslant 0 c⊤(x−Vopt)⩽0包含可行解集,沿着法向量的正向或反向即可找到约束下的最优值。
Seidel线性规划算法
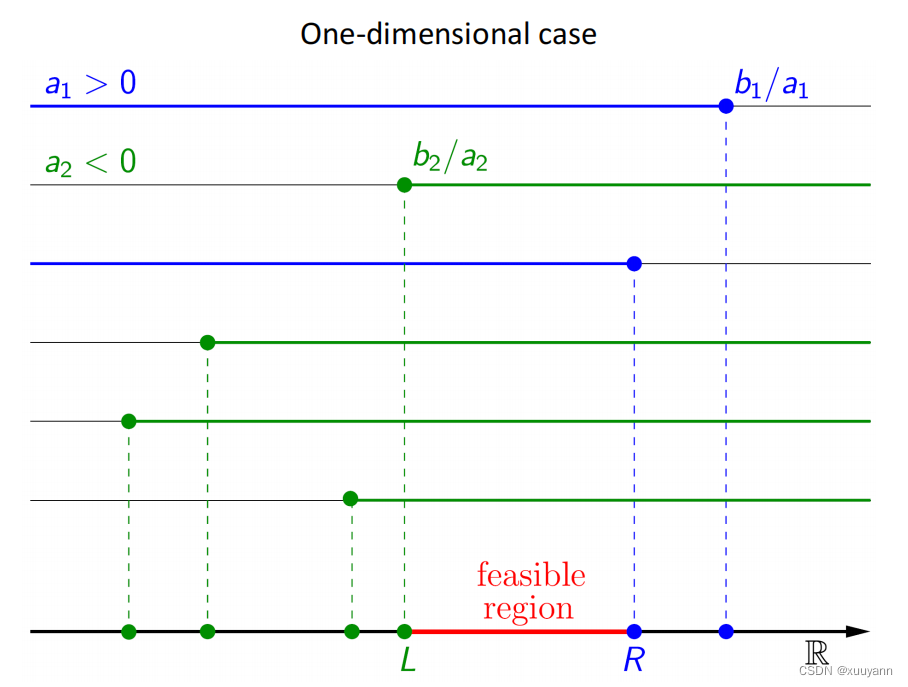
如下图所示,一维线性规划例子,很简单。

如下图所示,二维线性规划例子,也很简单。
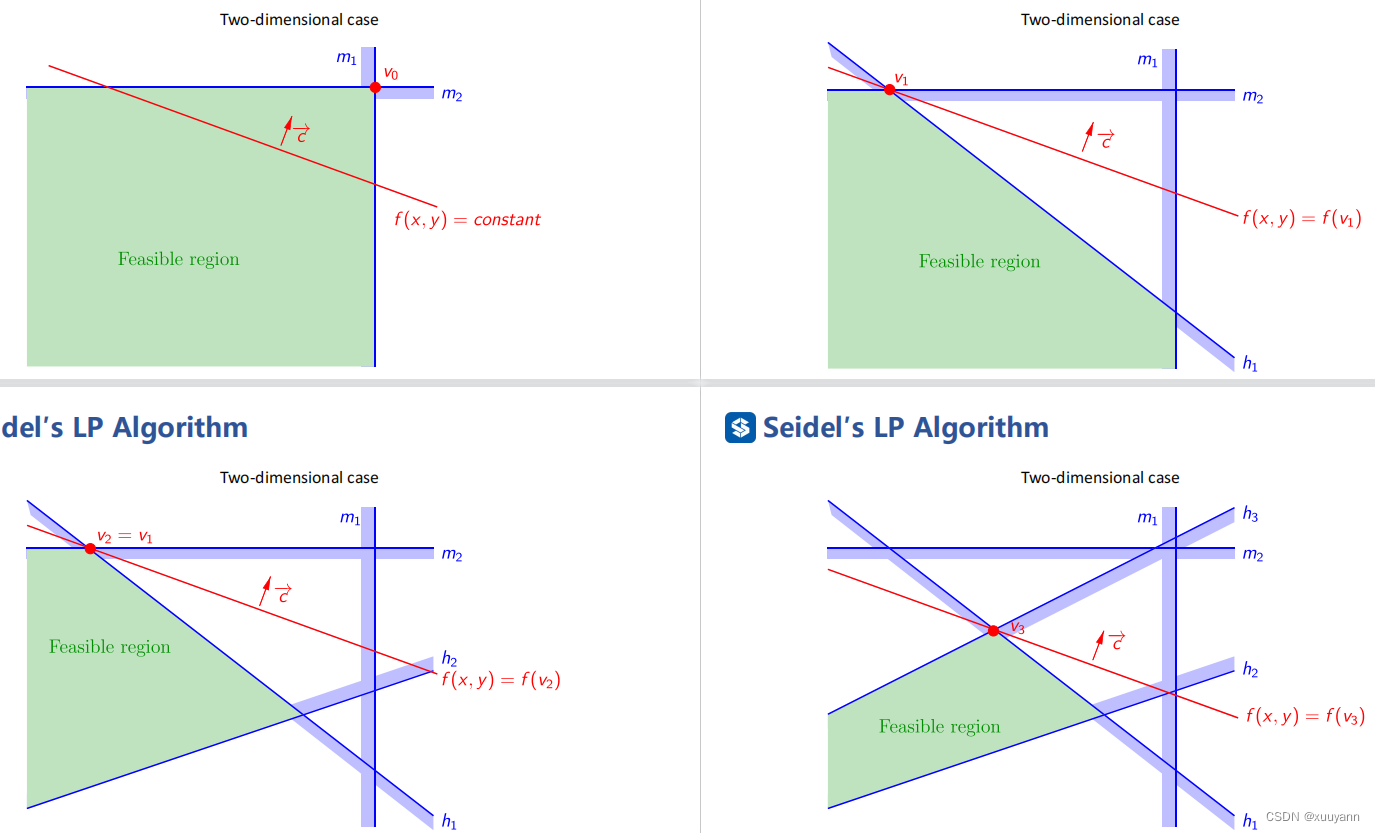
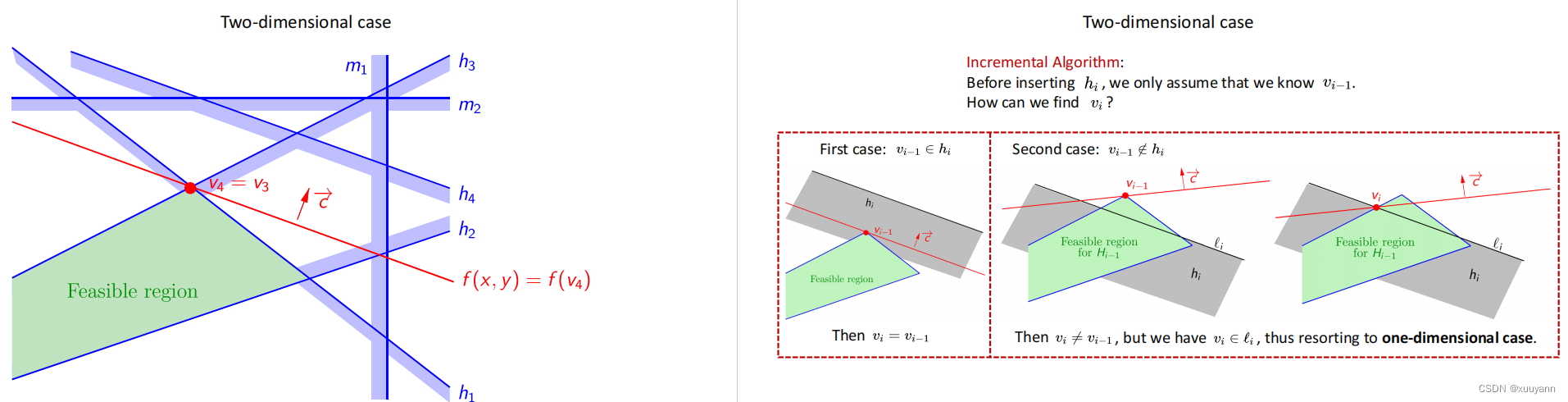
拓展到多维,可使用Seidel线性规划算法进行精确求解,适用于维度不高但约束很多的线性规划问题。Seidel‘s LP利用列主元高斯消元法将 d d d维线性规划问题投影到 d − 1 d-1 d−1维超平面空间内,时间复杂度为 O ( n ) O(n) O(n)。

低维严格凸二次规划问题
定义
一般形式如下所示,目标函数为二次型且严格凸即 M Q M_{\mathcal{Q}} MQ正定,约束函数为仿射(线性)时,称该问题为严格凸二次规划(QP)问题。对于严格凸二次规划问题, M Q M_{\mathcal{Q}} MQ正定则可以做Cholesky分解,可将原问题转换成解最小范数问题,从几何意义上可以理解为最优解就是可行解集凸多面体上与origin原点最近的点。

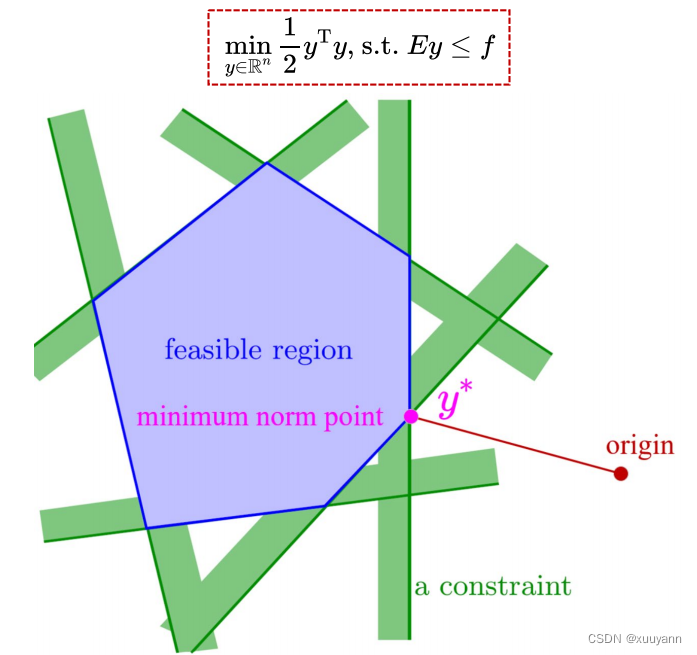
低维情况下的精确最小范数算法:将Seidel的算法从LP推广到严格凸的QP上。
先以简单的一维和二维为例。
一维情况:
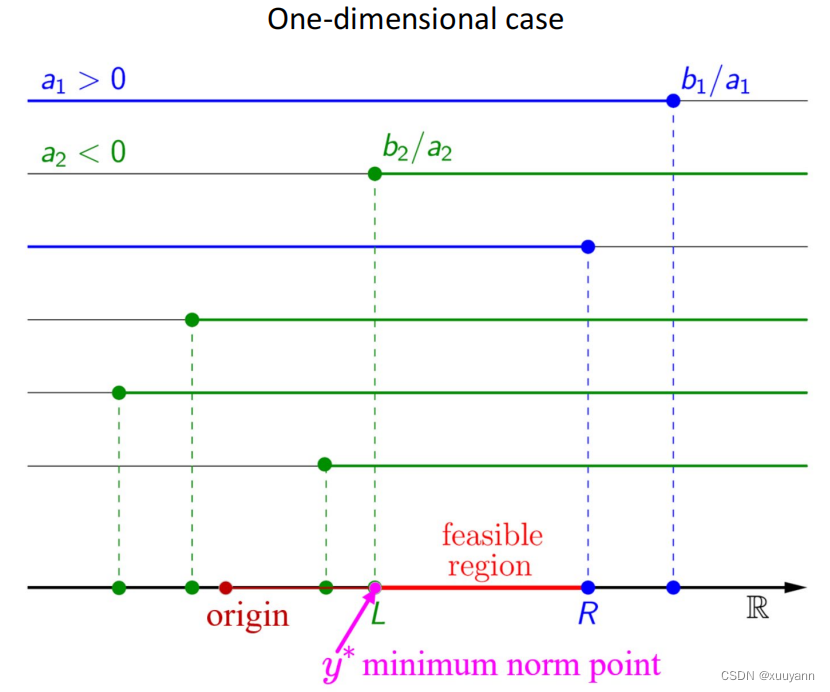
二维情况:
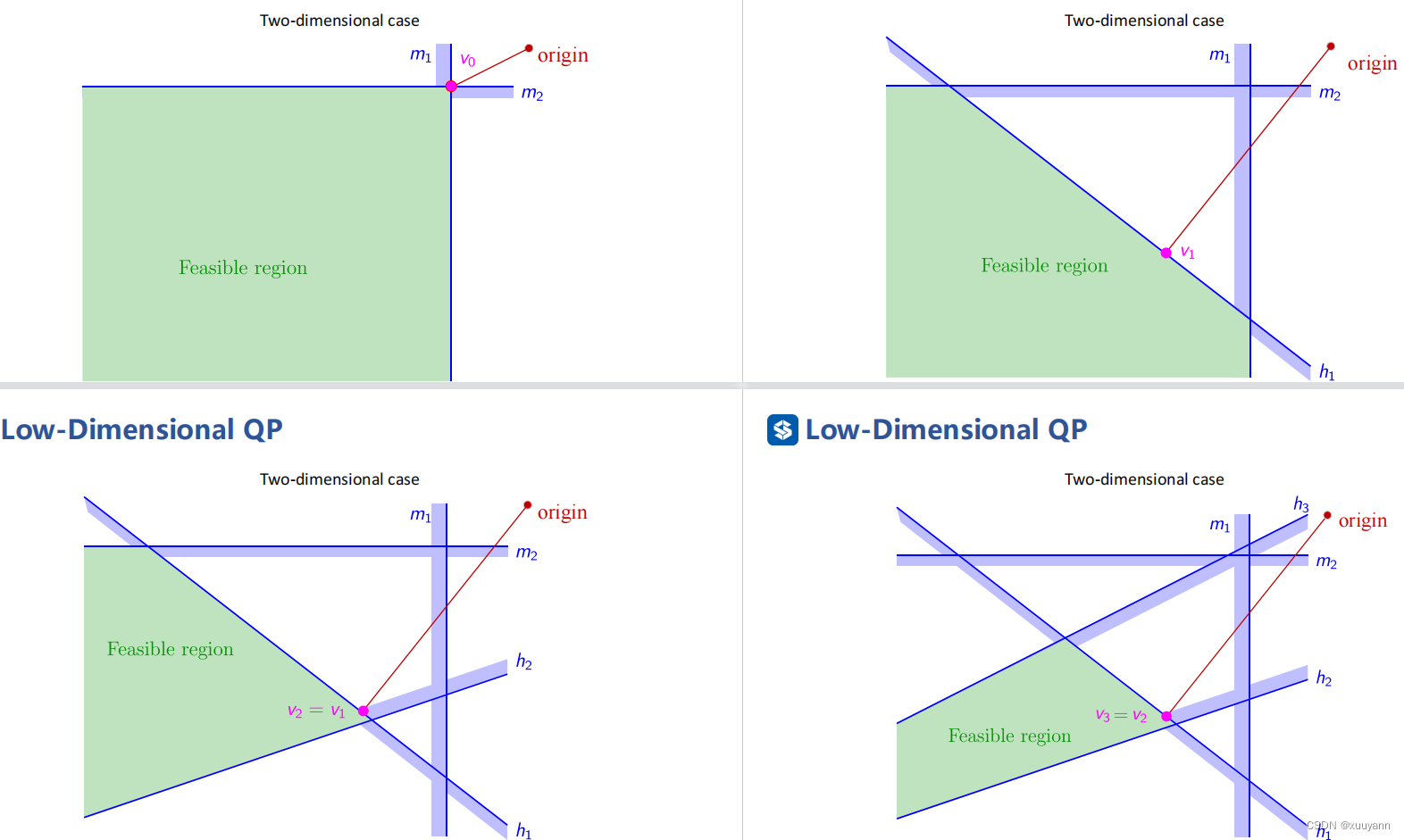
扩展到多维,算法伪代码如下图所示。其中,算法入参 H \mathcal{H} H表示约束 A y ≤ b Ay \leq b Ay≤b, A ∈ R n × d A \in \mathbb{R}^{n \times d} A∈Rn×d,
h h h表示包含解的超平面约束;
v ∈ R d v \in \mathbb{R}^d v∈Rd表示超平面约束内的最小范数点(迭代过程中的new origin);
M ∈ R d × ( d − 1 ) M \in \mathbb{R}^{d \times(d-1)} M∈Rd×(d−1)表示 h h h超平面上的一组标准正交基;
H ′ \mathcal{H}^{\prime} H′表示超平面约束 h h h上的 ( d − 1 ) (d-1) (d−1)维不等式,迭代更新的 H ′ \mathcal{H}^{\prime} H′可以参考前面一维二维例子中不断迭代更新的Feasible region。

第1~3行:若约束维度为1时,就是最简单的一维问题,直接解就行;若约束维度大于1,进入第4行;
第4行:迭代初始化一个空集 I \mathcal{I} I;
第5行:以随机顺序加入一个新的超平面约束 h ∈ H h \in \mathcal{H} h∈H, h : g T y = f h: g^{\mathrm{T}} y=f h:gTy=f,进入循环迭代;
第6行:如果满足前一迭代约束的最优解 y ∉ h y \notin h y∈/h,进行第7步;若 y ∈ h y \in h y∈h,表示新约束满足,进行第11行;
第7行:此时满足前一迭代约束的最优解
y
∉
h
y \notin h
y∈/h,
{
M
,
v
,
H
′
}
←
\left\{M, v, \mathcal{H}^{\prime}\right\} \leftarrow
{M,v,H′}← HouseholderProj
(
I
,
h
)
(\mathcal{I}, h)
(I,h)表示将
I
\mathcal{I}
I投影至
h
h
h约束上得到一个
(
d
−
1
)
(d-1)
(d−1)维问题(降维),并得到投影后的
(
d
−
1
)
(d-1)
(d−1)维不等式约束
H
′
\mathcal{H}^{\prime}
H′,进行第8行。对第7行进行详解,如下图所示,前一迭代为红色的Origin,直接求原Origin与不等式约束
H
′
\mathcal{H}^{\prime}
H′最近的点
y
∗
y^*
y∗很麻烦,但可以根据垂直距离最短和勾股定理间接计算:
∥
y
∗
−
o
∥
2
=
∥
y
∗
−
v
∥
2
+
∥
v
−
o
∥
2
\left\|y^*-o\right\|^2=\left\|y^*-v\right\|^2+\|v-o\|^2
∥y∗−o∥2=∥y∗−v∥2+∥v−o∥2
其中,
v
v
v表示前一迭代的Origin在新约束
h
h
h投影得到的New Origin。以
v
v
v为原点建立超平面约束
h
h
h的一组标准正交基
M
∈
R
d
×
(
d
−
1
)
M \in \mathbb{R}^{d \times(d-1)}
M∈Rd×(d−1)。以二维为例,
M
=
[
M
1
,
M
2
]
M=[M_1,M_2]
M=[M1,M2],则
y
∗
−
v
y^*-v
y∗−v是在
M
M
M构成的线性空间中的一个向量:
y
∗
−
v
=
M
1
y
1
′
+
M
2
y
2
′
=
[
M
1
M
2
]
[
y
1
′
y
2
′
]
=
M
y
′
y^*-v=M_1 y_1^{\prime}+M_2 y_2^{\prime}=\left[\begin{array}{ll}M_1 & M_2\end{array}\right]\left[\begin{array}{l}y_1^{\prime} \\ y_2^{\prime}\end{array}\right]=My^{\prime}
y∗−v=M1y1′+M2y2′=[M1M2][y1′y2′]=My′
其中,
y
′
∈
R
(
d
−
1
)
×
1
y^{\prime} \in \mathbb{R}^{(d-1) \times 1}
y′∈R(d−1)×1表示
y
∗
y^*
y∗在
M
M
M构成线性空间中的坐标。因为
M
T
M
=
I
M^\mathrm{T}M=I
MTM=I,则有:
∥
y
∗
−
o
∥
2
=
∥
y
∗
∥
2
=
∥
M
y
′
∥
2
+
∥
v
−
o
∥
2
=
∥
y
′
∥
2
+
∥
v
−
o
∥
2
=
∥
y
∗
∥
2
\left\|y^*-o\right\|^2=\left\|y^*\right\|^2= \left\|M y^{\prime}\right\|^2+\|v-o\|^2=\left\|y^{\prime}\right\|^2+\|v-o\|^2=\left\|y^*\right\|^2
∥y∗−o∥2=∥y∗∥2=∥My′∥2+∥v−o∥2=∥y′∥2+∥v−o∥2=∥y∗∥2
最小化
∥
y
∗
∥
2
\left\|y^*\right\|^2
∥y∗∥2问题转换成最小化
∥
y
′
∥
2
\left\|y^{\prime}\right\|^2
∥y′∥2,实现了优化问题的降维。

问题1:如何求集合 I \mathcal{I} I投影到 h h h上的约束 H ′ \mathcal{H}^{\prime} H′?
已知 H \mathcal{H} H为超平面约束 A y ≤ b Ay \leq b Ay≤b,其中 A ∈ R n × d , y ∈ R d × 1 , b ∈ R n × 1 A \in \mathbb{R}^{n \times d}, y \in \mathbb{R}^{d \times 1}, b \in \mathbb{R}^{n \times 1} A∈Rn×d,y∈Rd×1,b∈Rn×1,在得到 M M M矩阵后,将 M y ′ + v = y My^{\prime}+v=y My′+v=y带入原约束 A y ≤ b Ay \leq b Ay≤b可得, A M y ′ + A v ≤ b AMy^{\prime}+Av \leq b AMy′+Av≤b,也即 A M y ′ ≤ b − A v AMy^{\prime} \leq b-Av AMy′≤b−Av,其中 M ∈ R d × ( d − 1 ) M \in \mathbb{R}^{d \times(d-1)} M∈Rd×(d−1), y ′ ∈ R ( d − 1 ) × 1 y^{\prime} \in \mathbb{R}^{(d-1) \times 1} y′∈R(d−1)×1, A M ∈ R n × ( d − 1 ) AM \in \mathbb{R}^{n \times(d-1)} AM∈Rn×(d−1), b − A v ∈ R n × 1 b-Av \in \mathbb{R}^{n \times 1} b−Av∈Rn×1。因此,求得降维后投影后的约束 H ′ : ( A M ) y ′ ≤ b − A v \mathcal{H}^{\prime}:(AM)y^{\prime} \leq b-Av H′:(AM)y′≤b−Av。
问题2:如何找到超平面 h : g T y = f h:g^{\mathrm T}y=f h:gTy=f上的一组标准正交基 M M M?
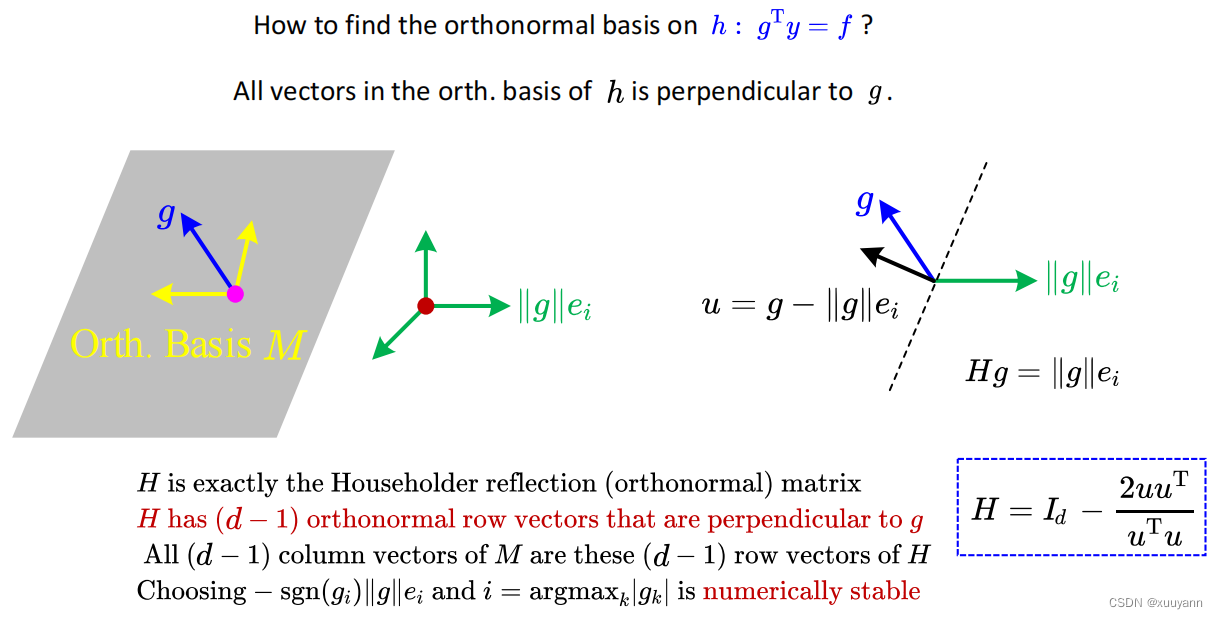
已知 g g g为超平面 h h h的法向,则可在构造一组标准正交基 ( e 1 , ⋅ ⋅ ⋅ , e i , ⋅ ⋅ ⋅ , e d ) (e_1,···,e_i,···,e_d) (e1,⋅⋅⋅,ei,⋅⋅⋅,ed),令 e i = ∥ g ∥ e i e_i=\|g\| e_i ei=∥g∥ei,显然 ( e 1 , ⋅ ⋅ ⋅ , ∥ g ∥ e i , ⋅ ⋅ ⋅ , e d ) (e_1,···,\|g\|e_i,···,e_d) (e1,⋅⋅⋅,∥g∥ei,⋅⋅⋅,ed)还是一组正交基,只要令 g g g与 ∥ g ∥ e i \|g\|e_i ∥g∥ei同向,则剩余的 ( e 1 ⋯ e d ⏟ d − 1 ) (\underbrace{e_1 \cdots e_d}_{d-1}) (d−1 e1⋯ed)即为要求的 M M M。
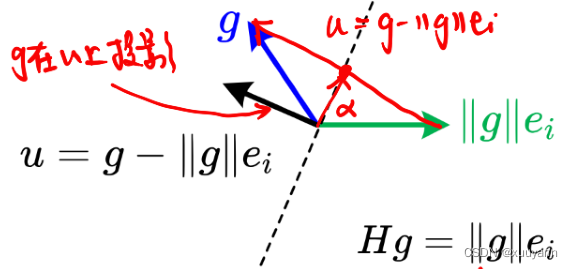
同向不好求,但可以利用反射变换进行间接求解,即令
g
g
g与
∥
g
∥
e
i
\|g\| e_i
∥g∥ei互为反射变换,满足映射关系
H
g
=
∥
g
∥
e
i
Hg=\|g\| e_i
Hg=∥g∥ei。如下图所示,以虚线为镜面,则
u
u
u为镜面的法向量,
u
=
g
−
∥
g
∥
e
i
u=g-\|g\| e_i
u=g−∥g∥ei,为了数值稳定性,选择投影方向为
−
sgn
(
g
i
)
∥
g
i
∥
e
i
-\operatorname{sgn}\left(g_i\right)\left\|g_i\right\| e_i
−sgn(gi)∥gi∥ei,其中
i
=
arg
max
k
∣
g
k
∣
i=\arg \max _k\left|g_k\right|
i=argmaxk∣gk∣,所以原始公式变为
u
=
g
+
sgn
(
g
i
)
∥
g
i
∥
e
i
u=g+\operatorname{sgn}\left(g_i\right)\left\|g_i\right\| e_i
u=g+sgn(gi)∥gi∥ei。黑色向量为
g
g
g在
u
u
u上的投影,为
g
T
u
∥
u
∥
u
∥
u
∥
g^{\mathrm{T}}\frac{u}{\|u\|}\frac{u}{\|u\|}
gT∥u∥u∥u∥u,则:
∥
g
∥
e
i
=
g
−
g
T
u
∥
u
∥
u
∥
u
∥
−
g
T
u
∥
u
∥
u
∥
u
∥
=
g
−
2
⋅
g
T
u
∥
u
∥
u
∥
u
∥
=
(
I
d
−
2
u
u
T
u
T
u
)
g
=
H
g
\begin{aligned} \|g\| e_i &=g-g^{\mathrm{T}}\frac{u}{\|u\|} \frac{u}{\|u\|}-g^{\mathrm{T}}\frac{u}{\|u\|} \frac{u}{\|u\|} \\ & =g-2 \cdot g^{\mathrm{T}} \frac{u}{\|u\|}\frac{u}{\|u\|} \\ & =\left(I_d-\frac{2 u u^{\mathrm{T}}}{u^{\mathrm{T}} u}\right) g \\ & = Hg \end{aligned}
∥g∥ei=g−gT∥u∥u∥u∥u−gT∥u∥u∥u∥u=g−2⋅gT∥u∥u∥u∥u=(Id−uTu2uuT)g=Hg
即,反射矩阵
H
=
(
I
d
−
2
u
u
T
u
T
u
)
H=\left(I_d-\frac{2 u u^{\mathrm{T}}}{u^{\mathrm{T}} u}\right)
H=(Id−uTu2uuT)。将
H
H
H按行分块,可得:
H
g
=
∥
g
∥
e
i
=
(
α
1
T
⋮
α
i
−
1
T
α
i
T
α
i
+
1
T
⋮
α
d
T
)
g
=
(
0
⋮
0
∥
g
∥
0
⋮
0
)
H g=\|g\| e_i=\left(\begin{array}{c} \alpha_1^{\mathrm{T}} \\ \vdots \\ \alpha_{i-1}^{\mathrm{T}} \\ \hdashline \alpha_i^{\mathrm{T}} \\ \hdashline \alpha_{i+1}^{\mathrm{T}} \\ \vdots \\ \alpha_d^{\mathrm{T}} \end{array}\right) g = \left(\begin{array}{c} 0 \\ \vdots \\ 0 \\ \|g\| \\ 0 \\ \vdots \\ 0 \end{array}\right)
Hg=∥g∥ei=
α1T⋮αi−1TαiTαi+1T⋮αdT
g=
0⋮0∥g∥0⋮0
根据上述分析,可得
α
i
T
g
=
∥
g
∥
\alpha_i^{\mathrm{T}} g=\|g\|
αiTg=∥g∥,
α
j
≠
i
T
g
=
0
\alpha_{j \neq i}^{\mathrm{T}} g=0
αj=iTg=0,因此求得
M
=
(
α
1
⋯
α
i
−
1
,
α
i
+
1
⋯
α
d
)
∈
R
d
×
(
d
−
1
)
M=\left(\alpha_1 \cdots \alpha_{i-1}, \alpha_{i+1} \cdots \alpha_d\right) \in \mathbb{R}^{d \times(d-1)}
M=(α1⋯αi−1,αi+1⋯αd)∈Rd×(d−1)。
第8行: y ′ ← y^{\prime} \leftarrow y′← LowDimMinNorm ( H ′ ) \left(\mathcal{H}^{\prime}\right) (H′),根据第7步的降维操作后进行递归,递推推出条件为解出第1~3步的一维最优化问题。在求出降维后的 d − 1 d-1 d−1维最优解 y ′ y^{\prime} y′后,进行第9步;
第9行:通过 y = M y ′ + v y=My^{\prime}+v y=My′+v计算得到 d d d维最优解 y y y,进行第11行。
第11行:将超平面约束 h h h收入到集合 I \mathcal{I} I中,跳转第5行,执行下一个循环迭代。
c++代码
参考代码:ZJU-FAST-Lab/SDQP
代码对投影降维过程进行了简化:为了加快求解速度,不直接求解反射矩阵H,直接求投影后的不等式约束 H ′ : ( A M ) y ′ ≤ b − A v \mathcal{H}^{\prime}:(AM)y^{\prime} \leq b-Av H′:(AM)y′≤b−Av。设不等式约束个数为n,优化量的维度为d, c = − 2 u T u c=-\frac{2}{\mathbf{u}^{\mathrm{T}} \mathbf{u}} c=−uTu2, u = ( u 1 , u 2 , u 3 , … , u d ) T \mathbf{u}=\left(u_1, u_2, u_3, \ldots, u_d\right)^{\mathrm{T}} u=(u1,u2,u3,…,ud)T,
对原约束系数矩阵
A
A
A进行行分块:
A
=
[
a
11
a
12
a
13
…
a
1
d
a
21
a
22
a
23
…
a
2
d
a
31
a
32
a
33
…
a
3
d
⋮
⋮
⋮
⋮
a
n
1
a
n
2
a
n
3
…
a
n
d
]
n
×
d
=
[
A
1
A
2
A
3
⋮
A
n
]
\mathbf{A}=\left[\begin{array}{ccccc} a_{11} & a_{12} & a_{13} & \ldots & a_{1 d} \\ a_{21} & a_{22} & a_{23} & \ldots & a_{2 d} \\ a_{31} & a_{32} & a_{33} & \ldots & a_{3 d} \\ \vdots & \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & a_{n 3} & \ldots & a_{n d} \end{array}\right]_{n \times d}=\left[\begin{array}{c} \mathbf{A}_1 \\ \mathbf{A}_2 \\ \mathbf{A}_3 \\ \vdots \\ \mathbf{A}_n \end{array}\right]
A=
a11a21a31⋮an1a12a22a32⋮an2a13a23a33⋮an3…………a1da2da3d⋮and
n×d=
A1A2A3⋮An
计算反射矩阵
H
H
H:
H
=
I
d
+
c
[
u
1
u
1
u
1
u
2
u
1
u
3
…
u
1
u
d
u
2
u
1
u
2
u
2
u
2
u
3
…
u
2
u
d
u
3
u
1
u
3
u
2
u
3
u
3
…
u
3
u
d
⋮
u
d
u
1
u
d
u
2
u
d
u
3
…
u
d
u
d
]
=
I
d
+
c
u
T
u
\mathbf{H}=\mathbf{I}_d+c\left[\begin{array}{ccccc} u_1 u_1 & u_1 u_2 & u_1 u_3 & \ldots & u_1 u_d \\ u_2 u_1 & u_2 u_2 & u_2 u_3 & \ldots & u_2 u_d \\ u_3 u_1 & u_3 u_2 & u_3 u_3 & \ldots & u_3 u_d \\ \vdots & & & & \\ u_d u_1 & u_d u_2 & u_d u_3 & \ldots & u_d u_d \end{array}\right]=\mathbf{I}_d+c \mathbf{u}^{\mathrm{T}} \mathbf{u}
H=Id+c
u1u1u2u1u3u1⋮udu1u1u2u2u2u3u2udu2u1u3u2u3u3u3udu3…………u1udu2udu3ududud
=Id+cuTu
假设
g
g
g中第二个元素的绝对值最大,去掉
H
H
H中的第二行,则矩阵
M
M
M为:
M
=
[
1
0
…
0
0
0
…
0
0
1
…
0
⋮
⋮
⋮
0
0
…
1
]
+
c
[
u
1
u
1
u
3
u
1
…
u
d
u
1
u
1
u
2
u
3
u
2
…
u
d
u
2
u
1
u
3
u
3
u
3
…
u
d
u
3
⋮
⋮
⋮
u
1
u
d
u
3
u
d
…
u
d
u
d
]
d
×
(
d
−
1
)
=
I
′
+
c
[
U
1
U
3
…
U
d
]
\mathbf{M}=\left[\begin{array}{cccc} 1 & 0 & \ldots & 0 \\ 0 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \ldots & 1 \end{array}\right]+c\left[\begin{array}{cccc} u_1 u_1 & u_3 u_1 & \ldots & u_d u_1 \\ u_1 u_2 & u_3 u_2 & \ldots & u_d u_2 \\ u_1 u_3 & u_3 u_3 & \ldots & u_d u_3 \\ \vdots & \vdots & & \vdots \\ u_1 u_d & u_3 u_d & \ldots & u_d u_d \end{array}\right]_{d \times(d-1)}=\mathbf{I}^{\prime}+c\left[\begin{array}{lllll} \mathbf{U}_1 & \mathbf{U}_3 & \ldots & \left.\mathbf{U}_d\right] \end{array}\right.
M=
100⋮0001⋮0…………000⋮1
+c
u1u1u1u2u1u3⋮u1udu3u1u3u2u3u3⋮u3ud…………udu1udu2udu3⋮udud
d×(d−1)=I′+c[U1U3…Ud]
投影后:
A
′
=
A
M
=
[
a
11
a
12
a
13
…
a
1
d
a
21
a
22
a
23
…
a
2
d
⋮
⋮
⋮
⋮
a
n
1
a
n
2
a
n
3
…
a
n
d
]
(
[
1
0
…
0
0
0
…
0
0
1
…
0
⋮
⋮
⋮
0
0
…
1
]
+
c
[
u
1
u
1
u
3
u
1
…
u
d
u
1
u
1
u
2
u
3
u
2
…
u
d
u
2
u
1
u
3
u
3
u
3
…
u
d
u
3
⋮
⋮
⋮
u
1
u
d
u
3
u
d
…
u
d
u
d
]
)
=
[
a
11
a
13
…
a
1
d
a
21
a
23
…
a
2
d
⋮
⋮
⋮
a
n
1
a
n
3
…
a
n
d
]
+
c
[
a
11
u
1
u
1
+
a
12
u
1
u
2
+
a
13
u
1
u
3
+
⋯
+
a
1
d
u
1
u
d
…
a
21
u
1
u
1
+
a
22
u
1
u
2
+
a
23
u
1
u
3
+
⋯
+
a
2
d
u
1
u
d
…
⋮
a
n
1
u
1
u
1
+
a
n
2
u
1
u
2
+
a
n
3
u
1
u
3
+
⋯
+
a
n
d
u
1
u
d
…
]
=
[
a
11
a
13
…
a
1
d
a
21
a
23
…
a
2
d
⋮
⋮
⋮
a
n
1
a
n
3
…
a
n
d
]
+
c
[
A
1
U
1
A
1
U
3
…
A
1
U
d
A
2
U
1
A
2
U
3
…
A
2
U
d
⋮
⋮
⋮
A
n
U
n
A
n
U
3
…
A
n
U
d
]
\begin{aligned} & \mathbf{A}^{\prime}=\mathbf{A} \mathbf{M} \\ & =\left[\begin{array}{ccccc} a_{11} & a_{12} & a_{13} & \ldots & a_{1 d} \\ a_{21} & a_{22} & a_{23} & \ldots & a_{2 d} \\ \vdots & \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & a_{n 3} & \ldots & a_{n d} \end{array}\right]\left(\left[\begin{array}{cccc} 1 & 0 & \ldots & 0 \\ 0 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \ldots & 1 \end{array}\right]+c\left[\begin{array}{cccc} u_1 u_1 & u_3 u_1 & \ldots & u_d u_1 \\ u_1 u_2 & u_3 u_2 & \ldots & u_d u_2 \\ u_1 u_3 & u_3 u_3 & \ldots & u_d u_3 \\ \vdots & \vdots & & \vdots \\ u_1 u_d & u_3 u_d & \ldots & u_d u_d \end{array}\right]\right) \\ & =\left[\begin{array}{cccc} a_{11} & a_{13} & \ldots & a_{1 d} \\ a_{21} & a_{23} & \ldots & a_{2 d} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 3} & \ldots & a_{n d} \end{array}\right]+c\left[\begin{array}{cc} a_{11} u_1 u_1+a_{12} u_1 u_2+a_{13} u_1 u_3+\cdots+a_{1 d} u_1 u_d & \ldots \\ a_{21} u_1 u_1+a_{22} u_1 u_2+a_{23} u_1 u_3+\cdots+a_{2 d} u_1 u_d & \ldots \\ \vdots \\ a_{n 1} u_1 u_1+a_{n 2} u_1 u_2+a_{n 3} u_1 u_3+\cdots+a_{n d} u_1 u_d & \ldots \end{array}\right] \\ & =\left[\begin{array}{cccc} a_{11} & a_{13} & \ldots & a_{1 d} \\ a_{21} & a_{23} & \ldots & a_{2 d} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 3} & \ldots & a_{n d} \end{array}\right]+c\left[\begin{array}{cccc} \mathbf{A}_1 \mathbf{U}_1 & \mathbf{A}_1 \mathbf{U}_3 & \ldots & \mathbf{A}_1 \mathbf{U}_d \\ \mathbf{A}_2 \mathbf{U}_1 & \mathbf{A}_2 \mathbf{U}_3 & \ldots & \mathbf{A}_2 \mathbf{U}_d \\ \vdots & \vdots & & \vdots \\ \mathbf{A}_n \mathbf{U}_n & \mathbf{A}_n \mathbf{U}_3 & \ldots & \mathbf{A}_n \mathbf{U}_d \end{array}\right] \\ & \end{aligned}
A′=AM=
a11a21⋮an1a12a22⋮an2a13a23⋮an3………a1da2d⋮and
100⋮0001⋮0…………000⋮1
+c
u1u1u1u2u1u3⋮u1udu3u1u3u2u3u3⋮u3ud…………udu1udu2udu3⋮udud
=
a11a21⋮an1a13a23⋮an3………a1da2d⋮and
+c
a11u1u1+a12u1u2+a13u1u3+⋯+a1du1uda21u1u1+a22u1u2+a23u1u3+⋯+a2du1ud⋮an1u1u1+an2u1u2+an3u1u3+⋯+andu1ud………
=
a11a21⋮an1a13a23⋮an3………a1da2d⋮and
+c
A1U1A2U1⋮AnUnA1U3A2U3⋮AnU3………A1UdA2Ud⋮AnUd
b ′ = b − A v = [ b 1 b 2 ⋮ b n ] − [ a 11 a 13 … a 1 d a 21 a 23 … a 2 d ⋮ ⋮ ⋮ a n 1 a n 3 … a n d ] [ v 1 v 2 ⋮ v d ] = [ b 1 − A 1 v b 2 − A 2 v ⋮ b n − A n v ] \begin{aligned} \mathbf{b}^{\prime} & =\mathbf{b}-\mathbf{A} \mathbf{v} \\ & =\left[\begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_n \end{array}\right]-\left[\begin{array}{cccc} a_{11} & a_{13} & \ldots & a_{1 d} \\ a_{21} & a_{23} & \ldots & a_{2 d} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 3} & \ldots & a_{n d} \end{array}\right]\left[\begin{array}{c} v_1 \\ v_2 \\ \vdots \\ v_d \end{array}\right]=\left[\begin{array}{c} b_1-\mathbf{A}_1 \mathbf{v} \\ b_2-\mathbf{A}_2 \mathbf{v} \\ \vdots \\ b_n-\mathbf{A}_n \mathbf{v} \end{array}\right] \end{aligned} b′=b−Av= b1b2⋮bn − a11a21⋮an1a13a23⋮an3………a1da2d⋮and v1v2⋮vd = b1−A1vb2−A2v⋮bn−Anv
代码及关键注释如下:
/*
MIT License
Copyright (c) 2022 Zhepei Wang (wangzhepei@live.com)
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.
*/
#ifndef SDQP_HPP
#define SDQP_HPP
#include <Eigen/Eigen>
#include <cmath>
#include <random>
namespace sdqp
{
constexpr double eps = 1.0e-12;
enum
{
MINIMUM = 0, ///< 有解
INFEASIBLE, ///< 无解
};
template <int d>
/**
* @brief set_zero 赋值为0
*/
inline void set_zero(double *x)
{
for (int i = 0; i < d; ++i)
{
x[i] = 0.0;
}
return;
}
template <int d>
/**
* @brief dot 点乘
*/
inline double dot(const double *x,
const double *y)
{
double s = 0.0;
for (int i = 0; i < d; ++i)
{
s += x[i] * y[i];\mathbf{I}
}
return s;
}
template <int d>
inline double sqr_norm(const double *x)
{
double s = 0.0;
for (int i = 0; i < d; ++i)
{
s += x[i] * x[i];
}
return s;
}
template <int d>
/**
* @brief mul 数乘
*/
inline void mul(const double *x,
const double s,
double *y)
{
for (int i = 0; i < d; ++i)
{
y[i] = x[i] * s;
}
return;
}
template <int d>
/**
* @brief max_abs 求向量中最大绝对值
*/
inline int max_abs(const double *x)
{
int id = 0;
double mag = std::fabs(x[0]);
for (int i = 1; i < d; ++i)
{
const double s = std::fabs(x[i]);
if (s > mag)
{
id = i;
mag = s;
}
}
return id;
}
template <int d>
inline void cpy(const double *x,
double *y)
{
for (int i = 0; i < d; ++i)
{
y[i] = x[i];
}
return;
}
inline int move_to_front(const int i,
int *next,
int *prev)
{
if (i == 0 || i == next[0])
{
return i;
}
const int previ = prev[i];
next[prev[i]] = next[i];
prev[next[i]] = prev[i];
next[i] = next[0];
prev[i] = 0;
prev[next[i]] = i;
next[0] = i;
return previ;
}
template <int d>
/**
* @brief min_norm
* @param halves 约束增广矩阵[A,-b]
* @param n 约束的维度
* @param m 前一迭代最优解违反约束的索引
* @param opt 满足约束的最优解
* @param work 约束空间地址
* @param next
* @param prev
* @return
*/
inline int min_norm(const double *halves,
const int n,
const int m,
double *opt,
double *work,
int *next,
int *prev)
{
int status = MINIMUM;
set_zero<d>(opt);
if (m <= 0)
{
return status;
}
double *reflx = work;
double *new_opt = reflx + d;
double *new_halves = new_opt + (d - 1);
double *new_work = new_halves + n * d; // 给下一迭代过程中的约束增广矩阵开辟新的地址
for (int i = 0; i != m; i = next[i])
{
const double *plane_i = halves + (d + 1) * i; // 第i个超平面约束
// opt违反了第i个超平面约束 A_ix-b > 0
if (dot<d>(opt, plane_i) + plane_i[d] > (d + 1) * eps)
{
const double s = sqr_norm<d>(plane_i);
if (s < (d + 1) * eps * eps)
{
return INFEASIBLE;
}
mul<d>(plane_i, -plane_i[d] / s, opt); // 求new_origin=fg/(g^(T)g)
if (i == 0)
{
continue;
}
// stable Householder reflection with pivoting
// 选择绝对值最大元素的index作为投影的方向
const int id = max_abs<d>(opt);
const double xnorm = std::sqrt(sqr_norm<d>(opt));
cpy<d>(opt, reflx);
// u = g + sgn(g_i)||g_i||*e_i
reflx[id] += opt[id] < 0.0 ? -xnorm : xnorm; // 镜面的法向量u=reflx
// H = I_d + hu^(T)u
const double h = -2.0 / sqr_norm<d>(reflx);
// 将之前的约束I都投影到选定的约束hi上,所以遍历到i平面马上退出
for (int j = 0; j != i; j = next[j])
{
double *new_plane = new_halves + d * j; // 投影后的约束增广矩阵[AM,-b+Av]
const double *old_plane = halves + (d + 1) * j; // 原约束增广矩阵[A,-b],按行分块
// 投影后的约束变为AM和b-Av,为加快求解速度,不直接求H
const double coeff = h * dot<d>(old_plane, reflx);
for (int k = 0; k < d; ++k)
{
const int l = k < id ? k : k - 1; // 用于去掉H矩阵中的第id行,往前挪一位
new_plane[l] = k != id ? old_plane[k] + reflx[k] * coeff : new_plane[l]; // A'=AM
}
// 投影后的约束为d-1维,正常应该是b'=b-Av,但这里传入的是-b',old_plane[d]=-b
new_plane[d - 1] = dot<d>(opt, old_plane) + old_plane[d];
}
// 降维后进行递归
status = min_norm<d - 1>(new_halves, n, i, new_opt, new_work, next, prev);
if (status == INFEASIBLE)
{
return INFEASIBLE;
}
double coeff = 0.0;
for (int j = 0; j < d; ++j)
{
const int k = j < id ? j : j - 1;
coeff += j != id ? reflx[j] * new_opt[k] : 0.0;
}
coeff *= h;
for (int j = 0; j < d; ++j)
{
const int k = j < id ? j : j - 1;
opt[j] += j != id ? new_opt[k] + reflx[j] * coeff : reflx[j] * coeff;
}
i = move_to_front(i, next, prev);
}
}
return status;
}
template <>
/**
* @brief min_norm<_Tp1> 解一维最小范数问题
*/
inline int min_norm<1>(const double *halves,
const int n,
const int m,
double *opt,
double *work,
int *next,
int *prev)
{
opt[0] = 0.0;
bool l = false;
bool r = false;
for (int i = 0; i != m; i = next[i])
{
const double a = halves[2 * i];
const double b = halves[2 * i + 1];
if (a * opt[0] + b > 2.0 * eps)
{
if (std::fabs(a) < 2.0 * eps)
{
return INFEASIBLE;
}
l = l || a < 0.0;
r = r || a > 0.0;
if (l && r)
{
return INFEASIBLE;
}
opt[0] = -b / a;
}
}
return MINIMUM;
}
inline void rand_permutation(const int n,
int *p)
{
typedef std::uniform_int_distribution<int> rand_int;
typedef rand_int::param_type rand_range;
static std::mt19937_64 gen;
static rand_int rdi(0, 1);
int j, k;
for (int i = 0; i < n; ++i)
{
p[i] = i;
}
for (int i = 0; i < n; ++i)
{
rdi.param(rand_range(0, n - i - 1));
j = rdi(gen) + i;
k = p[j];
p[j] = p[i];
p[i] = k;
}
}
template <int d>
/**
* @brief sdmn 求解转换后的最小范数问题,新约束Ax <= b
* @return
*/
inline double sdmn(const Eigen::Matrix<double, -1, d> &A,
const Eigen::Matrix<double, -1, 1> &b,
Eigen::Matrix<double, d, 1> &x)
{
x.setZero(); // 初始化最小值为0
const int n = b.size(); // 约束的维度
if (n < 1)
{
return 0.0;
}
Eigen::VectorXi perm(n - 1);
Eigen::VectorXi next(n);
Eigen::VectorXi prev(n + 1);
if (n > 1)
{
rand_permutation(n - 1, perm.data());
prev(0) = 0;
next(0) = perm(0) + 1;
prev(perm(0) + 1) = 0;
for (int i = 0; i < n - 2; ++i)
{
next(perm(i) + 1) = perm(i + 1) + 1;
prev(perm(i + 1) + 1) = perm(i) + 1;
}
next(perm(n - 2) + 1) = n;
}
else
{
prev(0) = 0;
next(0) = 1;
next(1) = 1;
}
Eigen::Matrix<double, d + 1, -1, Eigen::ColMajor> halves(d + 1, n);
Eigen::VectorXd work((n + 2) * (d + 2) * (d - 1) / 2 + 1 - d);
const Eigen::VectorXd scale = A.rowwise().norm();
halves.template topRows<d>() = (A.array().colwise() / scale.array()).transpose();
halves.template bottomRows<1>() = (-b.array() / scale.array()).transpose(); // 这里传入的是-b
const int status = min_norm<d>(halves.data(), n, n,
x.data(), work.data(),
next.data(), prev.data());
double minimum = INFINITY;
if (status != INFEASIBLE)
{
minimum = x.norm();
}
return minimum;
}
/**
* minimize 0.5 x' Q x + c' x
* subject to A x <= b
* Q must be positive definite
**/
template <int d>
inline double sdqp(const Eigen::Matrix<double, d, d> &Q,
const Eigen::Matrix<double, d, 1> &c,
const Eigen::Matrix<double, -1, d> &A,
const Eigen::Matrix<double, -1, 1> &b,
Eigen::Matrix<double, d, 1> &x)
{
Eigen::LLT<Eigen::Matrix<double, d, d>> llt(Q);
if (llt.info() != Eigen::Success)
{
return INFINITY;
}
// 对Q进行Cholesky分解,将严格凸QP问题转换为简单的最小范数问题
const Eigen::Matrix<double, -1, d> As = llt.matrixU().template solve<Eigen::OnTheRight>(A);
const Eigen::Matrix<double, d, 1> v = llt.solve(c);
const Eigen::Matrix<double, -1, 1> bs = A * v + b;
double minimum = sdmn<d>(As, bs, x);
if (!std::isinf(minimum))
{
llt.matrixU().template solveInPlace<Eigen::OnTheLeft>(x);
x -= v;
minimum = 0.5 * (Q * x).dot(x) + c.dot(x);
}
return minimum;
}
} // namespace sdqp
#endif
参考文献
机器人中的数值优化
最优化:建模、算法与理论/最优化计算方法
ZJU-FAST-Lab/SDQP