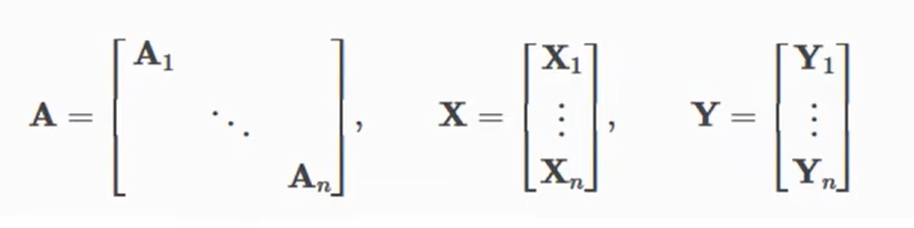线性回归

算法简述

线性回归是一种基本的机器学习算法，它用于建立自变量和因变量之间的线性关系模型。它假设自变量和因变量之间存在线性关系，通过最小化误差平方和来找到最优的模型参数，包括截距和斜率，以使模型的预测值尽可能地接近真实值。在实际应用中，线性回归算法广泛用于预测房价、股票价格、销售量等连续性数值型数据的预测问题。

LinearRegression() API

LinearRegression() 是一个基于最小二乘法的线性回归模型。它通过拟合一个线性方程来预测响应变量（因变量）和一个或多个解释变量（自变量）之间的关系。

LinearRegression() 可以通过一些参数进行调整来优化模型的性能，以下是其中一些常见的参数：

fit_intercept：是否计算截距。默认为 True。
normalize：是否对解释变量进行归一化。默认为 False。
copy_X：是否复制解释变量。默认为 True。
n_jobs：并行处理的数量。默认为 1。
positive：是否强制回归系数为正。默认为 False。

在实践中，一般使用默认参数即可，只有在特定的情况下，如当数据集非常大或者具有特定的特征时，才需要进行调整。

from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 加载糖尿病数据集
diabetes = load_diabetes()

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, test_size=0.2, random_state=42)

# 创建线性回归模型
model = LinearRegression()

# 训练模型
model.fit(X_train, y_train)

# 预测结果
y_pred = model.predict(X_test)

# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print("均方误差：", mse)
在这个例子中，我们首先加载了糖尿病数据集，然后使用 train_test_split 函数将数据集划分为训练集和测试集。接着，我们创建了一个线性回归模型，并使用训练集对模型进行训练。最后，我们使用测试集对模型进行测试，并计算出模型的均方误差。

需要注意的是，线性回归模型的性能很大程度上依赖于特征的选择和数据的预处理。在实际应用中，我们通常会对特征进行筛选和处理，以提高模型的预测准确性。

SGDRegressor API

SGDRegressor 是一种基于随机梯度下降法的线性回归模型。相较于传统的最小二乘法，它在大规模数据集下具有更好的计算效率和泛化性能。SGDRegressor 通过随机梯度下降算法来逐步调整回归系数，从而拟合数据集。它可以用于线性回归、L1正则化回归（Lasso）、L2正则化回归（Ridge）以及弹性网络回归（Elastic Net）等。

SGDRegressor 可以通过一些参数进行调整来优化模型的性能，以下是其中一些常见的参数：

loss：损失函数类型。默认为 'squared_loss'，即使用平方误差作为损失函数。也可以选择 'huber'、'epsilon_insensitive' 或 'squared_epsilon_insensitive'。
penalty：正则化类型。默认为 'l2'，即L2正则化。也可以选择 'l1' 或 'elasticnet'。
alpha：正则化强度。默认为 0.0001。
l1_ratio：当 penalty='elasticnet' 时，L1正则化的比例。默认为 0.15。
fit_intercept：是否计算截距。默认为 True。
learning_rate：学习率类型。默认为 'invscaling'，即随时间递减的学习率。也可以选择 'constant' 或 'optimal'。
eta0：学习率的初始值。默认为 0.01。
power_t：学习率的递减速率。默认为 0.25。
early_stopping：是否启用提前停止。默认为 False。
validation_fraction：提前停止时验证集的比例。默认为 0.1。
n_iter_no_change：连续多少次迭代损失函数未下降时停止迭代。默认为 5。
epsilon：当 loss='huber' 或 'epsilon_insensitive' 时，使用的 epsilon 值。默认为 0.1。

在实践中，SGDRegressor 的调参需要根据具体的数据集和任务来进行，一般需要进行多轮实验来找到最优参数组合。同时，使用随机梯度下降法进行模型训练时，需要仔细调节学习率等参数，以避免过拟合或欠拟合。

from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# 加载糖尿病数据集
diabetes = load_diabetes()

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, test_size=0.2, random_state=42)

# 线性回归模型
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)

# 在测试集上预测并评估模型
y_pred = lr_model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)

# 输出结果
print("均方误差：", mse)
在这个示例中，我们直接将糖尿病数据集划分为训练集和测试集，并使用 LinearRegression 进行线性回归。最后在测试集上计算均方误差。由于数据没有进行标准化处理，预测结果的单位与目标变量的单位相同，因此均方误差的量级也比标准化后的数据要大。

LinearRegression() 和 SGDRegressor对比

LinearRegression() 和 SGDRegressor 都是用于线性回归的算法。

LinearRegression() 是最基本的线性回归算法，它的实现基于最小二乘法。它通过拟合一个线性方程来预测响应变量（因变量）和一个或多个解释变量（自变量）之间的关系。在这种情况下，这个线性方程是一个一次函数，它可以表示为 y = a1x1 + a2x2 + … + anxn + b，其中 x1, x2, …, xn 是解释变量，y 是响应变量，a1, a2, …, an 是回归系数，b 是截距。在这种算法中，目标是找到最佳的回归系数和截距，以使误差最小化。它的计算比较简单，但如果数据集非常大，它的性能可能会受到影响。

相比之下，SGDRegressor 是一种基于随机梯度下降（SGD）的线性回归算法。它是一种迭代算法，每次迭代时只考虑一个样本，并在每次迭代中更新回归系数，直到达到最小化误差的目标。因此，它比 LinearRegression() 更适合大数据集，并且可以在线更新模型。SGDRegressor 可以支持不同类型的损失函数，如平方误差损失函数和 Huber 损失函数等。通过调整不同的超参数，如学习率和正则化参数，可以调整 SGDRegressor 的性能。

在实践中，如果数据集较小，使用 LinearRegression() 可能更容易实现，同时也更容易解释模型。如果数据集较大，则 SGDRegressor 更具有优势，因为它可以更快地收敛，并且可以在线更新模型。

下面是一个 LinearRegression 和 SGDRegressor 的对比示例：

from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.metrics import mean_squared_error

# 加载糖尿病数据集
diabetes = load_diabetes()

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, test_size=0.2, random_state=42)

# 线性回归模型
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)

# 随机梯度下降回归器
sgd_model = SGDRegressor(random_state=42)
sgd_model.fit(X_train, y_train)

# 在测试集上预测并评估模型
lr_pred = lr_model.predict(X_test)
lr_mse = mean_squared_error(y_test, lr_pred)

sgd_pred = sgd_model.predict(X_test)
sgd_mse = mean_squared_error(y_test, sgd_pred)

print(lr_mse,"  ",sgd_mse)

过拟合与欠拟合

过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)
欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)

岭回归

岭回归是一种用于处理多重共线性（即自变量之间存在高度相关性）和数据过拟合问题的线性回归模型。在标准的最小二乘线性回归中，当数据集存在多重共线性时，回归系数可能会出现很大的方差，导致预测结果不可靠；当模型复杂度过高时，也容易出现过拟合现象，导致模型在训练集上表现很好但在测试集上表现较差。

岭回归通过在损失函数中添加一个正则化项，对回归系数进行限制，从而减小方差，降低过拟合的风险。正则化项的大小由超参数α控制，α越大，正则化项的影响越大，回归系数越接近于0，从而减少方差的同时增加偏差。因此，超参数α的选择非常重要，通常需要通过交叉验证等方法进行调参。

在岭回归中，alpha是一个正则化参数，用于控制模型的复杂度。alpha的值越大，模型的正则化项的影响就越大，模型的复杂度就会降低，从而减少过拟合的风险。相反，如果alpha的值太小，模型就容易过拟合。因此，alpha需要通过交叉验证等技术进行调整，以找到最优的值。

下面是使用岭回归来解决过拟合和欠拟合问题的代码示例：

from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 加载数据集
boston = load_boston()
X, y = boston.data, boston.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 定义岭回归模型
ridge = Ridge()

# 定义超参数范围
params = {'alpha': [0.1, 1, 10, 100, 1000]}

# 使用网格搜索选择最优超参数
grid = GridSearchCV(estimator=ridge, param_grid=params, cv=5, scoring='neg_mean_squared_error')
grid.fit(X_train, y_train)

# 输出最优超参数和对应的负均方误差
print('Best alpha:', grid.best_params_['alpha'])
print('Best negative mean squared error:', grid.best_score_)

# 在测试集上评估模型性能
y_pred = grid.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print('Test set mean squared error:', mse)

在这个示例中，我们使用sklearn中的Ridge模型来进行岭回归，通过网格搜索来选择最优的超参数alpha，使用均方误差（MSE）作为评价指标。在最优超参数下，我们在测试集上得到了较低的MSE，说明岭回归可以有效地降低过拟合风险，提高模型泛化能力。

应用场景

线性回归是机器学习中最基础的模型之一，掌握它的原理和应用非常重要。除了前面讨论到的内容外，以下是一些可能有帮助的补充信息：

线性回归假设自变量和因变量之间的关系是线性的，因此在实际应用中，需要根据数据的特点来判断是否适合使用线性回归模型，或者是否需要对数据进行变换。
在实际应用中，线性回归模型往往需要进行特征工程来提高模型的预测性能。特征工程包括特征选择、特征变换、特征组合等技术，可以从数据中提取更有用的信息，以提高模型的准确性。
在处理非线性问题时，可以使用多项式回归模型，它通过对原始特征进行多项式变换来引入非线性项，从而拟合更加复杂的关系。不过需要注意的是，过高的多项式阶数可能会导致过拟合，因此需要通过交叉验证等技术来选择合适的阶数。
线性回归模型的性能指标通常采用均方误差（MSE）或平均绝对误差（MAE）等指标来衡量。在实际应用中，还需要考虑到模型的解释性、鲁棒性等因素来进行综合评估。
在使用线性回归模型时，需要注意数据集的划分和样本的随机性，否则可能会导致模型的偏差或方差过大，从而影响预测性能。