前言:本期学习是由datawhale(公众号)组织,由子豪兄讲解的202302期CS224图机器学习的学习笔记。本次学习为图嵌入表示学习,主要通过无监督或半监督的方法让图中的信息表示为指定尺寸向量。不用人工完成特征工程,与下游任务无关。主要针对矩阵分解和随机游走两种方法讲解图嵌入表示学习的过程。
图嵌入特点
输入为图输出为向量。
低纬 向量维度小于节点数
连续 元素均为实数
稠密 不会出现0元素
输出的向量与下游任务无关,由算法自主学习特征。
基本框架
编码器
输入节点,输出向量。
解码器
将向量计算之间的关系,检查是否符合原图的特点。(点之间的关系是否保存完整)
相似度计算方法:随机游走计算两个节点之间重复路径。
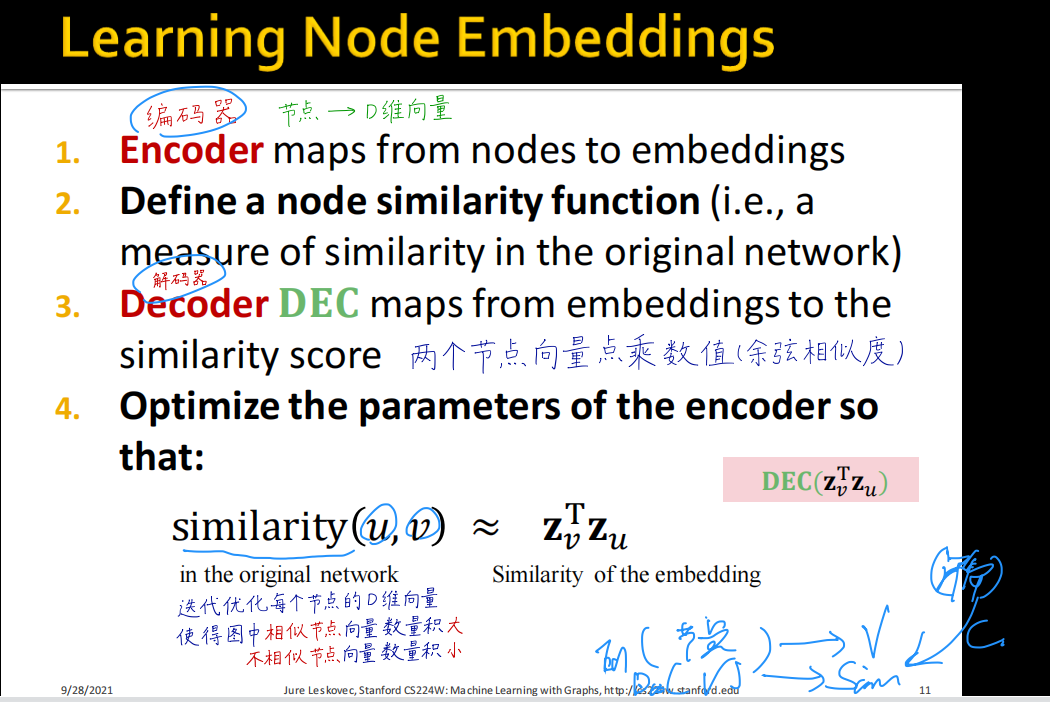


编码器解码器组合的目标:

随机游走算法
将图比作文章,随机游走序列就是句子。每个节点都是单词。随机游走的路径之间进行相似度计算,向量之间的积表示为相似关系。

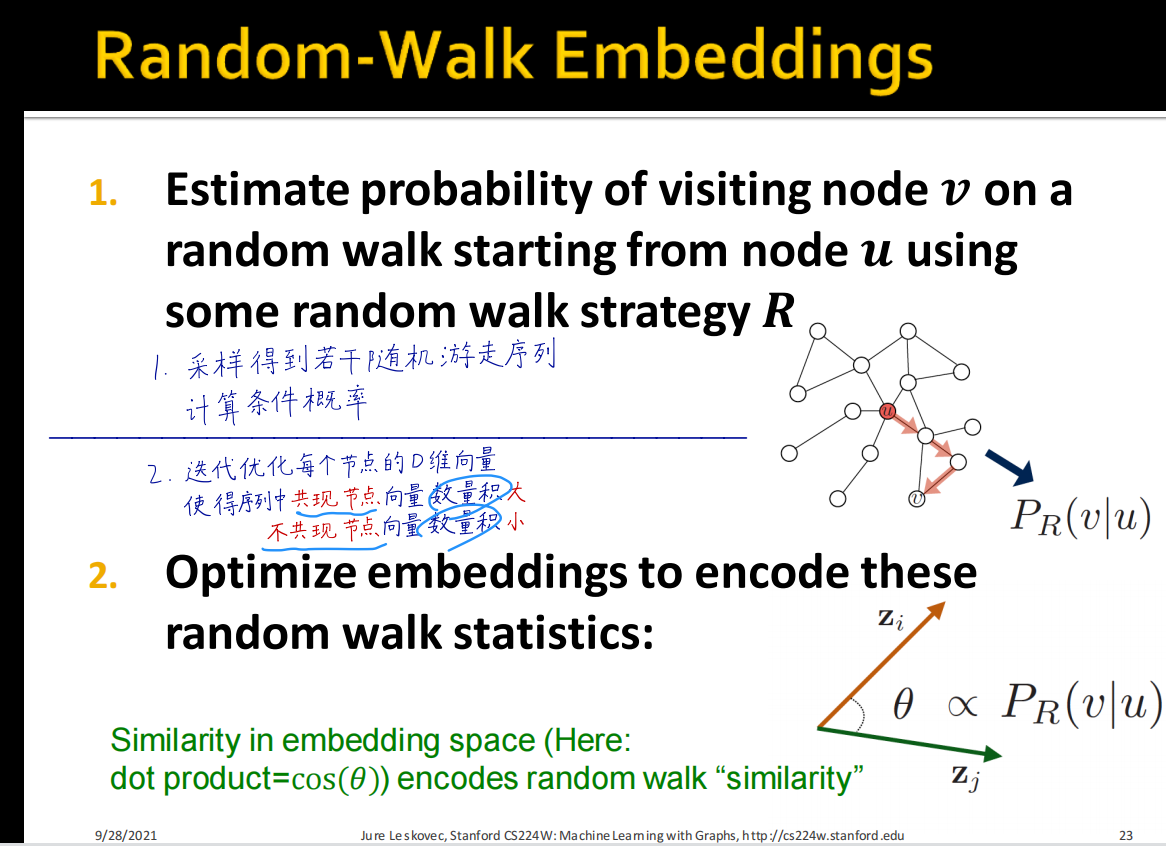
梯度下降方法让相似度达到最大化的思路是通过最大似然估计的角度,让预测准确度尽可能达到准确度最大值。


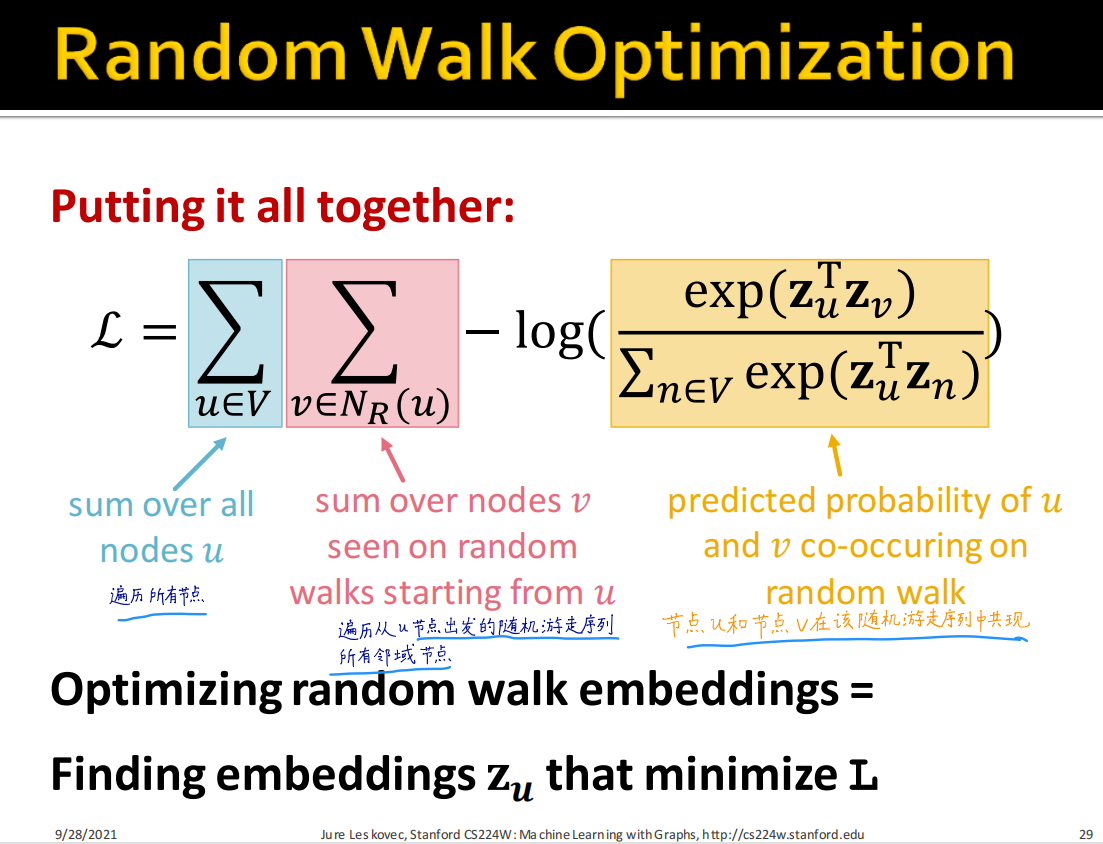
为了减少上式计算量,进行如下简化。将对数中分母部分的所有节点简化为部分节点计算(K个)。增加计算速度。


梯度优化
可以对每个节点求梯度后进行优化,也可对单一结单优化。
这里推荐折中方法,选择一批节点优化后迭代。

Node2Vec方法
Node2Vec其实是有偏二阶随机游走的方法。在随机游走的基础上增加深度和广度的概率偏执。通过偏执完成对下一跳的选择。
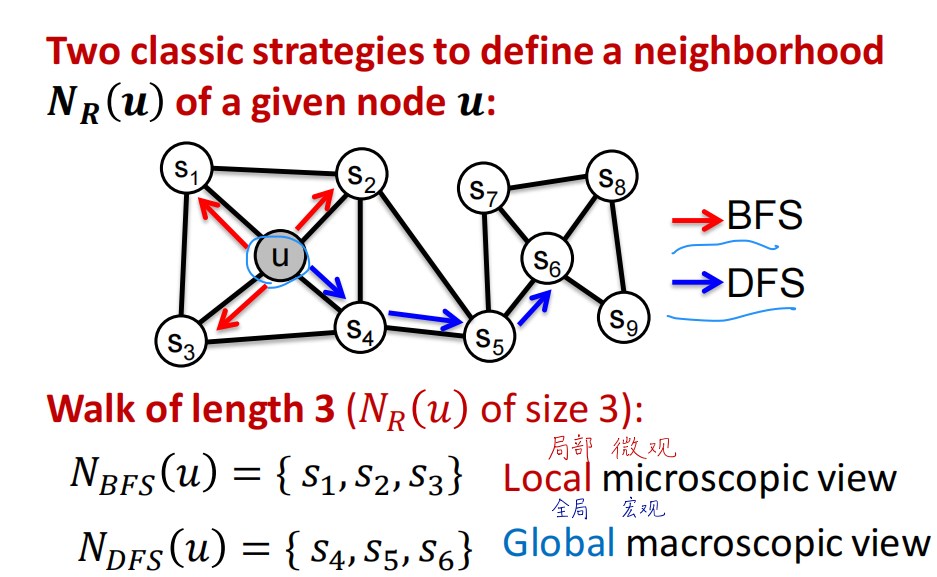
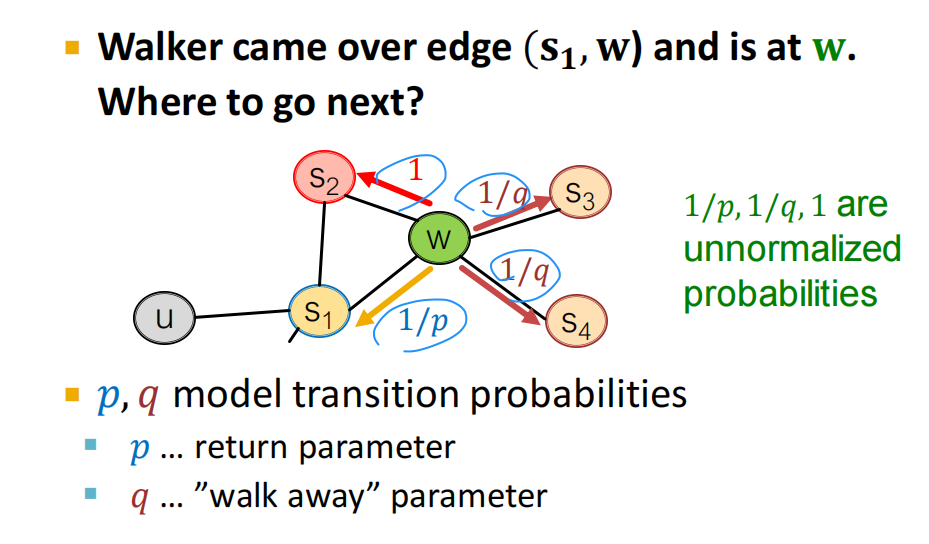
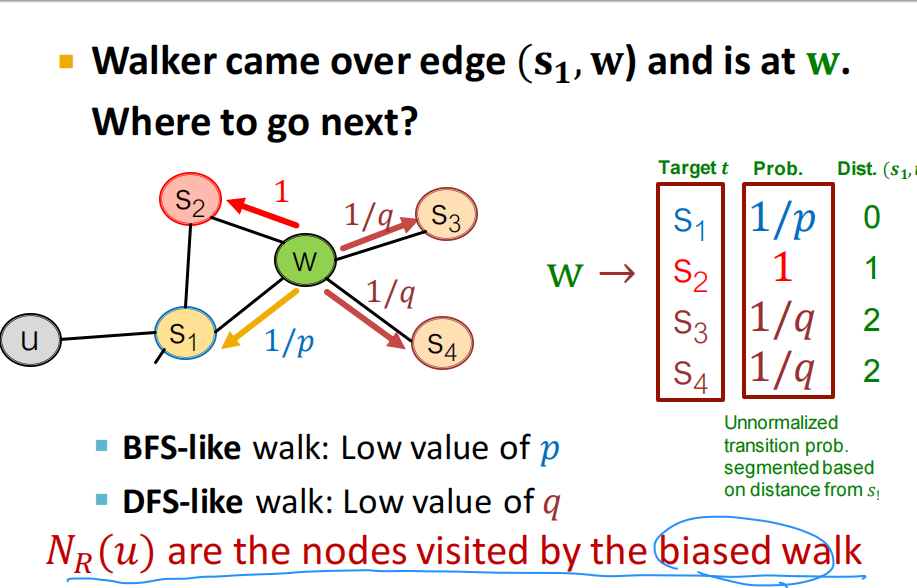
矩阵视角分析图嵌入和随机游走
目标向量的表示
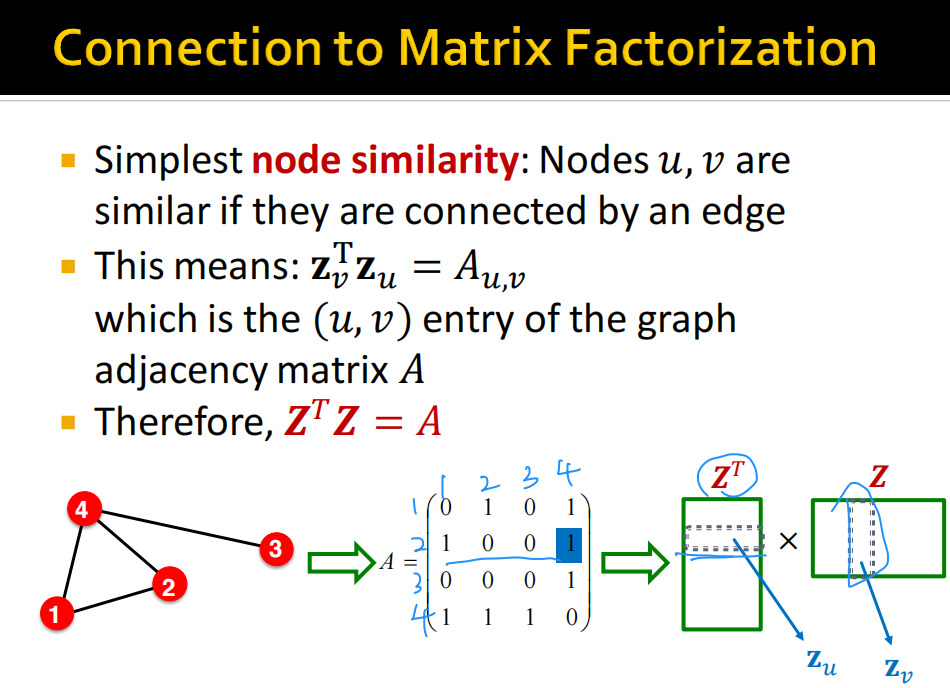
由于向量之间相乘并不是方阵相乘,进行二范数计算后得到相似度。

随机游走

Node2vec

总结


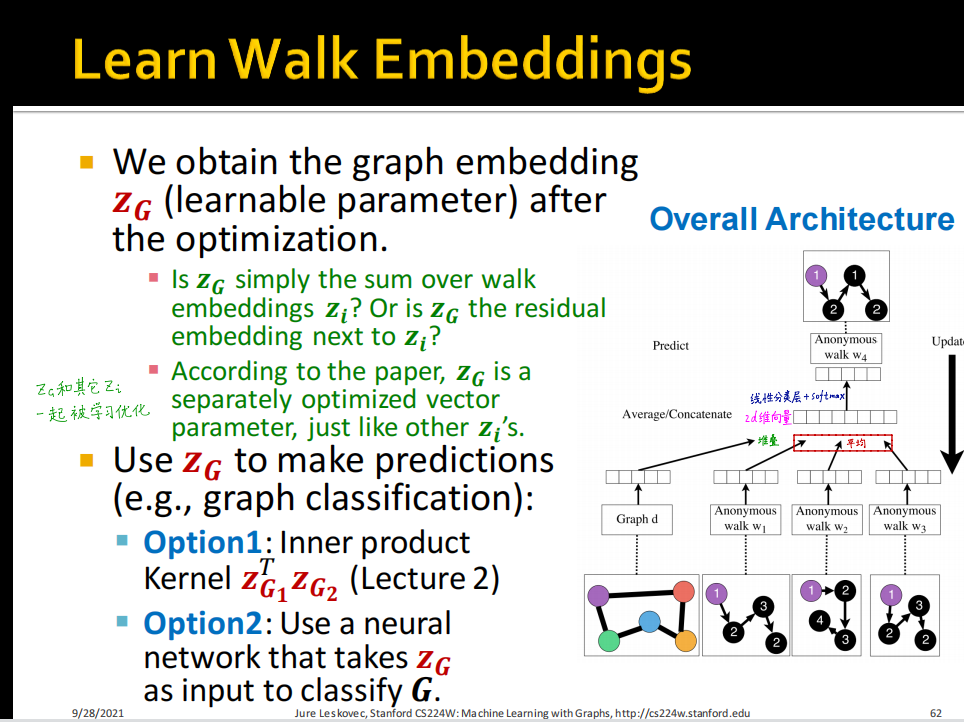
嵌入整张图
主要分为以下三步


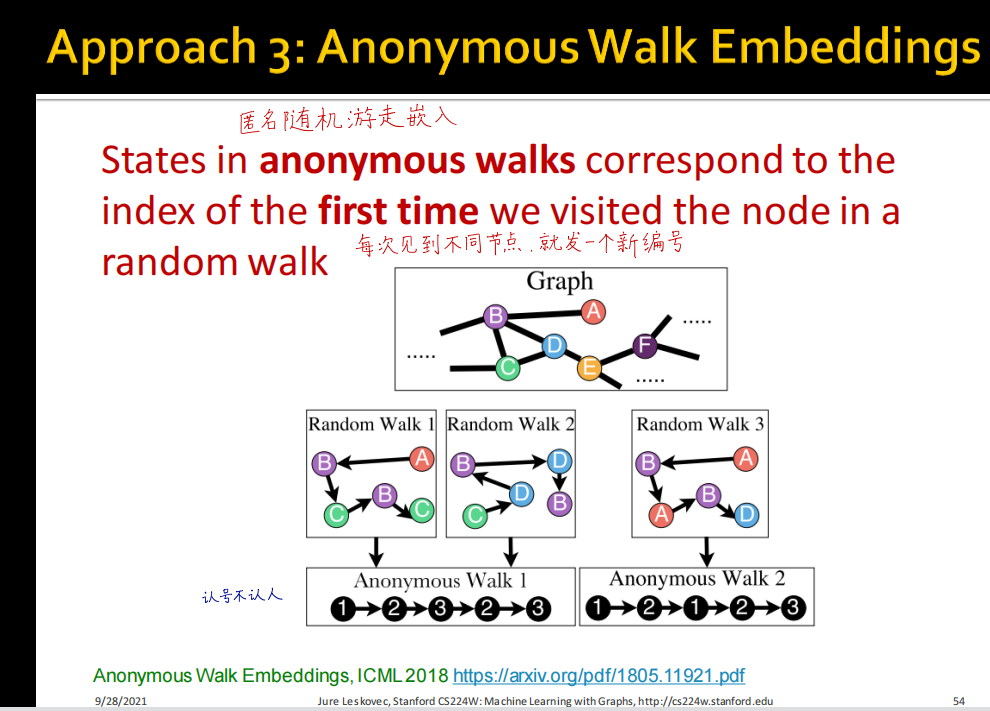
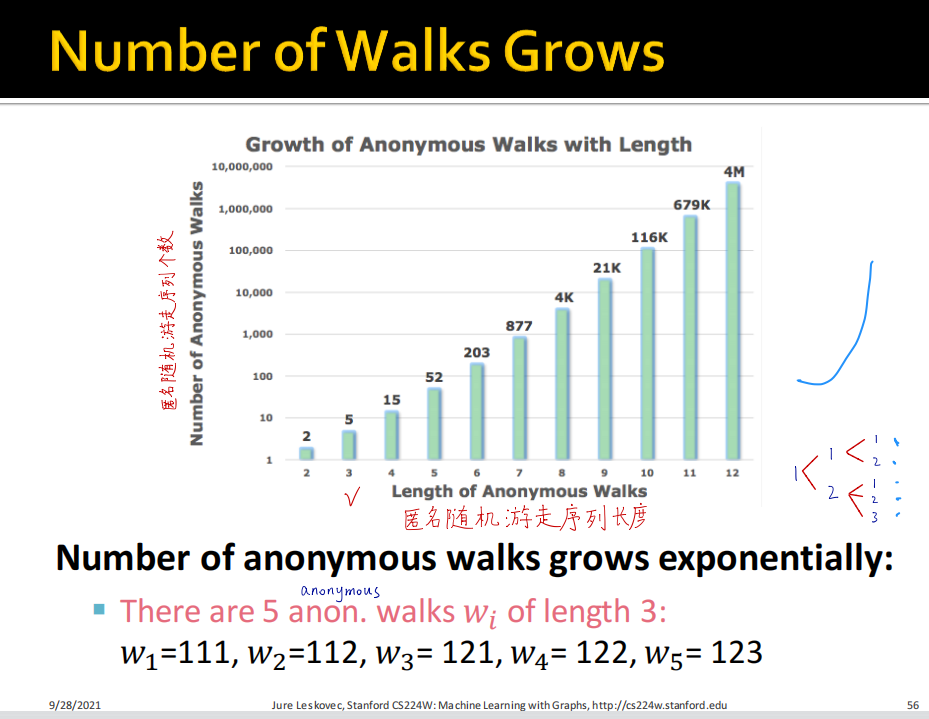
核心思路,比如对四个节点连接求另一个节点,将三个节点进行堆叠求平均,再求出新的向量