一、简介
树状数组 (Binary Indexed Tree,BIT),利用数的二进制特征进行检索的一种树状结构。
一种真正的高级数据结构: 二分思想、二叉树、位运算、前缀和。
高效!
代码极其简洁!
二、基本应用
数列a1,a2,....,an,操作:
单点修改:修改元素add(k,x): 把ak加上x。
求和:
sum (x) = a1 + ... + ax
区间和ai + ... + aj = sum(j) - sum(i-1)
三、不修改、只查询
数列aj, a2,..., an,求区间和: ai+ ...+aj
数列是静态的,用前缀和计算区间和,特别高效。
前缀和:sum[i]=a1+...+ ai
区间和: ai+...+aj = sum[j]-sum[i-1]
查询一次区间和,O(1)
代码


如果数列是动态的
修改元素add(k,x):把a加上x。
复杂度O(1)
求区间和:sum(j) - sum(i-1)
复杂度:O(n)--------->效率低
四、动态修改、求区间和: 用树状数组
数列是动态的
修改元素add(k,x):把ak加上x。
求区间和:sum(j) - sum(i-1)
复杂度都是: O(logn)
代码

五、从二叉树到树状数组
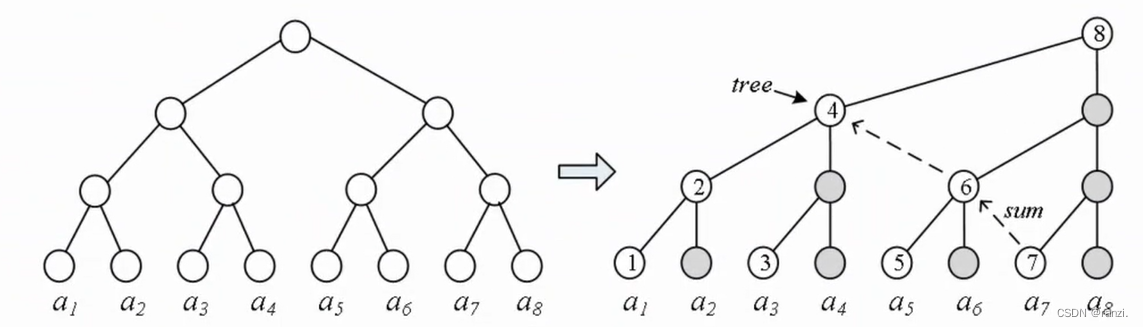
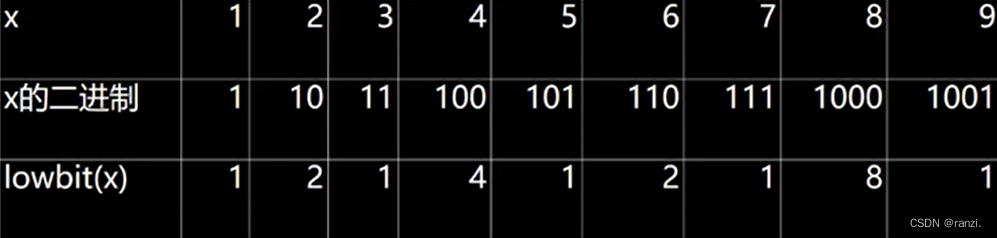
六、神奇的lowbit(x)操作
语法:lowbit(x)=x &-x
功能:找到x的二进制数的最后一个1
七、tree[ ]数组
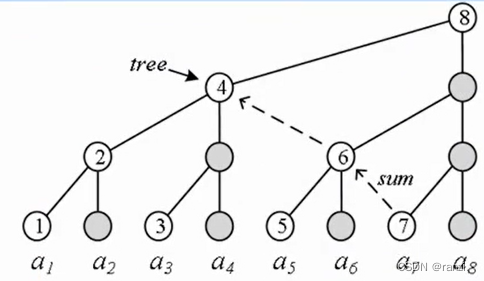
从lowbit(x)推出tree[ ]数组,所有的计算都基于tree[ ],令m =lowbit(x)。
定义tree[x]:把ax和它前面共m个数相加。
例: lowbit(6)=2,有tree[6] = a5+a6。

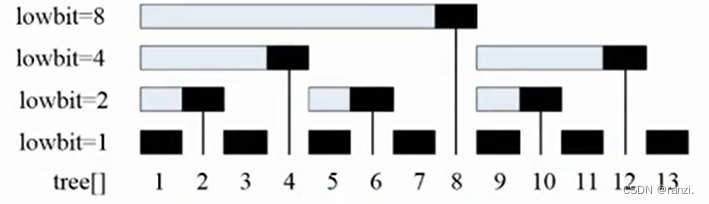
横线中的黑色表示tree[x],等于横线上元素相加的和。
八、基于tree[ ]的计算
求和sum=a1 +...+ax
利用tree[ ]数组求sum,例如:
sum[8] = tree[8]
sum[7] = tree[7] + tree[6] + tree[4]
sum[9] = tree[9] + tree[8]
以上关系是如何得到的?借助lowbit(x)。
九、sum[ ]的计算
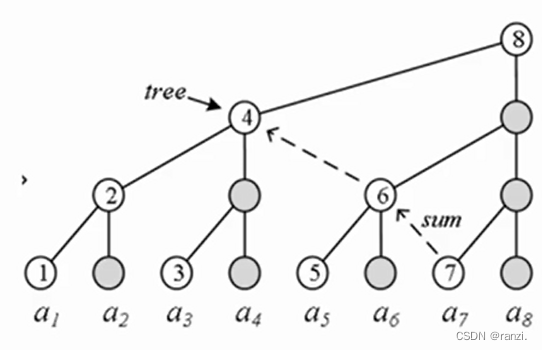
例: sum[7] = tree[7] + tree[6] + tree[4]
(1)从7开始,加上tree[7];
(2) 7 -lowbit(7)= 6,加上tree[6];
(3) 6 - lowbit(6) = 4,加上tree[4];
(4) 4-lowbit(4)= 0,结束。
sum()的复杂度?--------->O(logn)------非常好!
十、sum[ ]的更新
更改ax,和它相关的tree都会变化。
例如改变a3,那么tree[3]、tree[4]、tree[8]...都会改变。
影响哪些tree[ ]? 仍然利用lowbit(x)
(1) 更改tree[3];
(2) 3 +lowbit(3)= 4,更改tree[4];
(3) 4 +lowbit(4)=8,更改tree[8];
(4)直到最后的tree[n]。
复杂度?--------->O(logn)------非常好!