官网：http://zh.d2l.ai/
视频可以去b站找
记录的是个人觉得不太熟的知识

第二章 预备知识

代码地址：d2l-zh/pytorch/chapter_preliminaries

2.1 数据操作

2.1. 数据操作 — 动手学深度学习 2.0.0 documentation

如果只想知道张量中元素的总数，即形状的所有元素乘积，可以检查它的大小（size）。因为这里在处理的是一个向量，所以它的shape与它的size相同。

# x = torch.arange(12)
x.numel()

# 12

我们也可以把多个张量连结（concatenate）在一起，把它们端对端地叠起来形成一个更大的张量。我们只需要提供张量列表，并给出沿哪个轴连结。
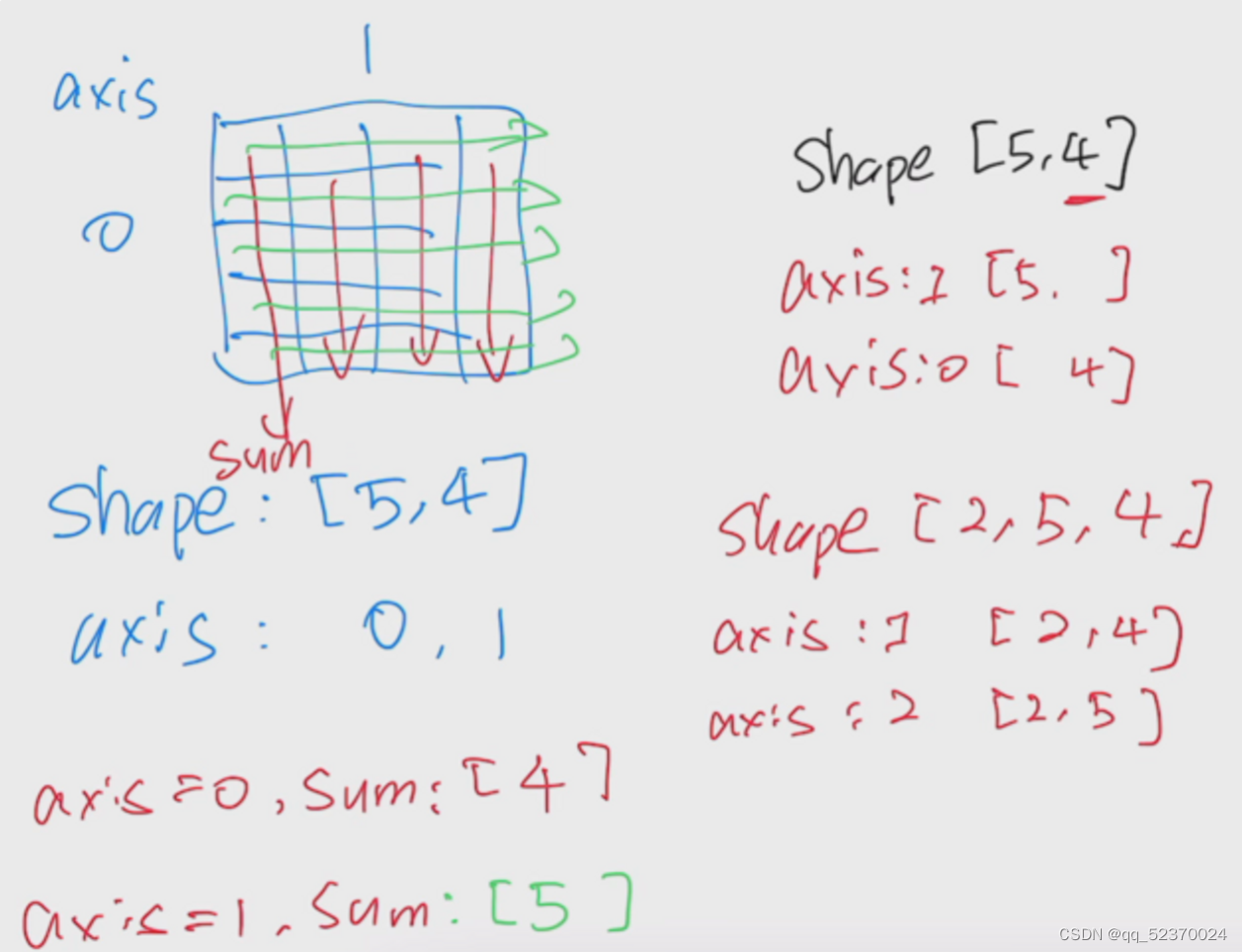
下面的例子分别演示了当我们沿行** （轴-0，形状的第一个元素）** 和按列**（轴-1，形状的第二个元素）**连结两个矩阵时，会发生什么情况。
我们可以看到，第一个输出张量的轴-0长度（6）是两个输入张量轴-0长度的总和（3+3）；第二个输出张量的轴-1长度（8）是两个输入张量轴-1长度的总和（4+4）。

X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)

# (tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [ 2.,  1.,  4.,  3.],
#         [ 1.,  2.,  3.,  4.],
#         [ 4.,  3.,  2.,  1.]]),
# tensor([[ 0.,  1.,  2.,  3.,  2.,  1.,  4.,  3.],
#         [ 4.,  5.,  6.,  7.,  1.,  2.,  3.,  4.],
#         [ 8.,  9., 10., 11.,  4.,  3.,  2.,  1.]]))

对张量中的所有元素进行求和，会产生一个单元素张量。

X.sum()

# tensor(66.)

广播机制

在上面的部分中，我们看到了如何在相同形状的两个张量上执行按元素操作。在某些情况下，即使形状不同，我们仍然可以通过调用广播机制（broadcasting mechanism）来执行按元素操作。
这种机制的工作方式如下：

1. 通过适当复制元素来扩展一个或两个数组，以便在转换之后，两个张量具有相同的形状；
2. 对生成的数组执行按元素操作。

在大多数情况下，我们将沿着数组中长度为1的轴进行广播，如下例子：

a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a, b

# (tensor([[0],
#         [1],
#         [2]]),
# tensor([[0, 1]]))

由于a和b分别是$3\times 1$和$1\times 2$矩阵，如果让它们相加，它们的形状不匹配。
我们将两个矩阵广播为一个更大的矩阵，如下所示：矩阵a将复制列，矩阵b将复制行，然后再按元素相加。

a + b

# tensor([[0, 1],
#        [1, 2],
#        [2, 3]])

节省内存

运行一些操作可能会导致为新结果分配内存。
例如，如果我们用Y = X + Y，我们将取消引用Y指向的张量，而是指向新分配的内存处的张量。

在下面的例子中，我们用Python的id()函数演示了这一点，它给我们提供了内存中引用对象的确切地址。运行Y = Y + X后，我们会发现id(Y)指向另一个位置。
这是因为Python首先计算Y + X，为结果分配新的内存，然后使Y指向内存中的这个新位置。

before = id(Y)
Y = Y + X
id(Y) == before

# False

这可能是不可取的，原因有两个：

1. 首先，我们不想总是不必要地分配内存。在机器学习中，我们可能有数百兆的参数，并且在一秒内多次更新所有参数。通常情况下，我们希望原地执行这些更新；
2. 如果我们不原地更新，其他引用仍然会指向旧的内存位置，这样我们的某些代码可能会无意中引用旧的参数。

幸运的是，执行原地操作非常简单。
我们可以使用切片表示法将操作的结果分配给先前分配的数组，例如Y[:] = <expression>。
为了说明这一点，我们首先创建一个新的矩阵Z，其形状与另一个Y相同，使用zeros_like来分配一个全的块。

Z = torch.zeros_like(Y)
print('id(Z):', id(Z))
Z[:] = X + Y
print('id(Z):', id(Z))

# id(Z): 139931132035296
# id(Z): 139931132035296

如果在后续计算中没有重复使用X，我们也可以使用X[:] = X + Y或X += Y来减少操作的内存开销。

before = id(X)
X += Y
id(X) == before

# True

转换为其他Python对象

将深度学习框架定义的张量转换为NumPy张量（ndarray）很容易，反之也同样容易。
torch张量和numpy数组将共享它们的底层内存，就地操作更改一个张量也会同时更改另一个张量。

A = X.numpy()
B = torch.tensor(A)
type(A), type(B)

# (numpy.ndarray, torch.Tensor)

要将大小为1的张量转换为Python标量，我们可以调用item函数或Python的内置函数。

a = torch.tensor([3.5])
a, a.item(), float(a), int(a)

# (tensor([3.5000]), 3.5, 3.5, 3)

2.2 数据预处理

2.2. 数据预处理 — 动手学深度学习 2.0.0 documentation

对于inputs中的类别值或离散值，我们将“NaN”视为一个类别。
由于“巷子类型”（“Alley”）列只接受两种类型的类别值“Pave”和“NaN”，pandas可以自动将此列转换为两列“Alley_Pave”和“Alley_nan”。巷子类型为“Pave”的行会将“Alley_Pave”的值设置为1，“Alley_nan”的值设置为0。缺少巷子类型的行会将“Alley_Pave”和“Alley_nan”分别设置为0和1。

#     NumRooms Alley
# 0       3.0  Pave
# 1       2.0   NaN
# 2       4.0   NaN
# 3       3.0   NaN

inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)

#       NumRooms  Alley_Pave  Alley_nan
# 0       3.0           1          0
# 1       2.0           0          1
# 2       4.0           0          1
# 3       3.0           0          1

注意

a = torch.arange(12)
b = a.reshape((3,4))
b[:] = 2
a

# tensor([2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
# 这里a的值发生了变化

2.3 线性代数

2.3. 线性代数 — 动手学深度学习 2.0.0 documentation

2.4 微积分

2.4. 微积分 — 动手学深度学习 2.0.0 documentation

2.5 自动微分

2.5. 自动微分 — 动手学深度学习 2.0.0 documentation

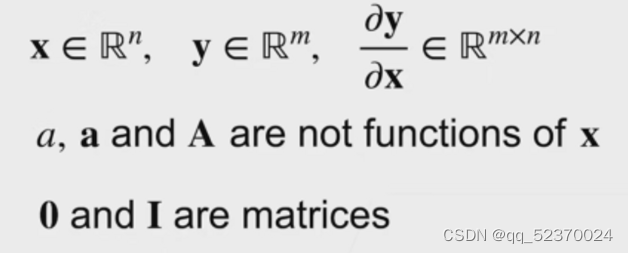
在默认情况下，PyTorch会累积梯度，我们需要清除之前的值

非标量变量的反向传播

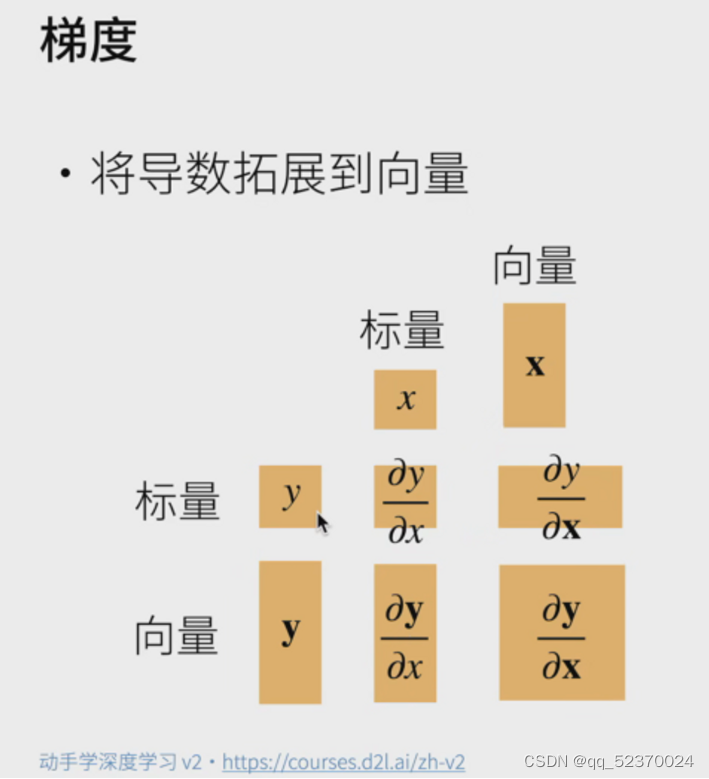
当y不是标量时，向量y关于向量x的导数的最自然解释是一个矩阵。

对于高阶和高维的y和x，求导的结果可以是一个高阶张量。

然而，虽然这些更奇特的对象确实出现在高级机器学习中（包括深度学习中），但当调用向量的反向计算时，我们通常会试图计算一批训练样本中每个组成部分的损失函数的导数。

这里，我们的目的不是计算微分矩阵，而是单独计算批量中每个样本的偏导数之和。

# 对非标量调用backward需要传入一个gradient参数，该参数指定微分函数关于self的梯度。
# 本例只想求偏导数的和，所以传递一个1的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad

# tensor([0., 2., 4., 6.])

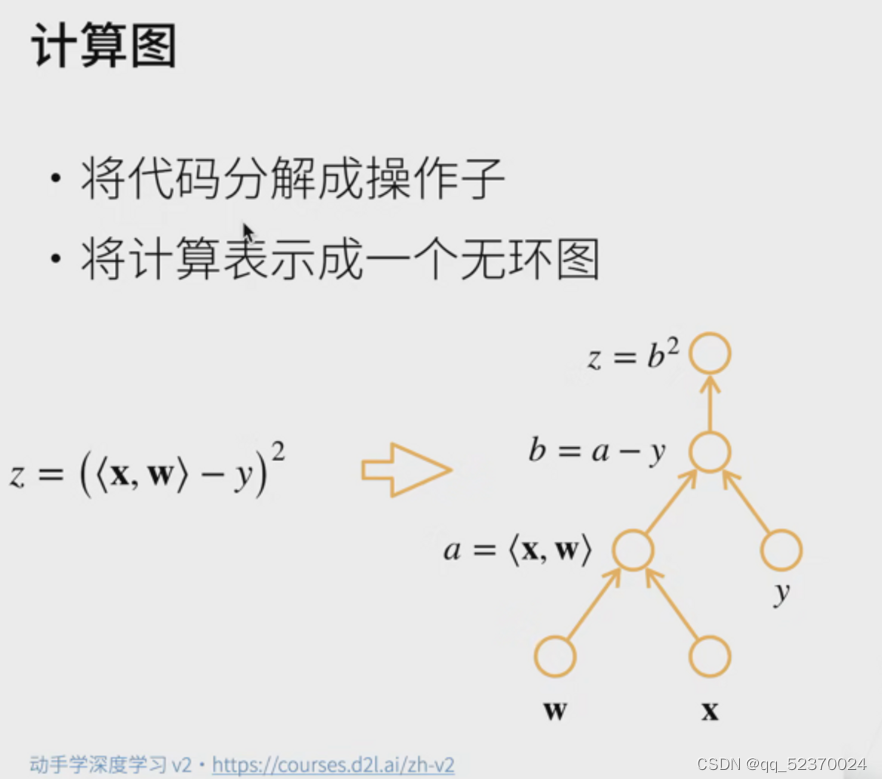
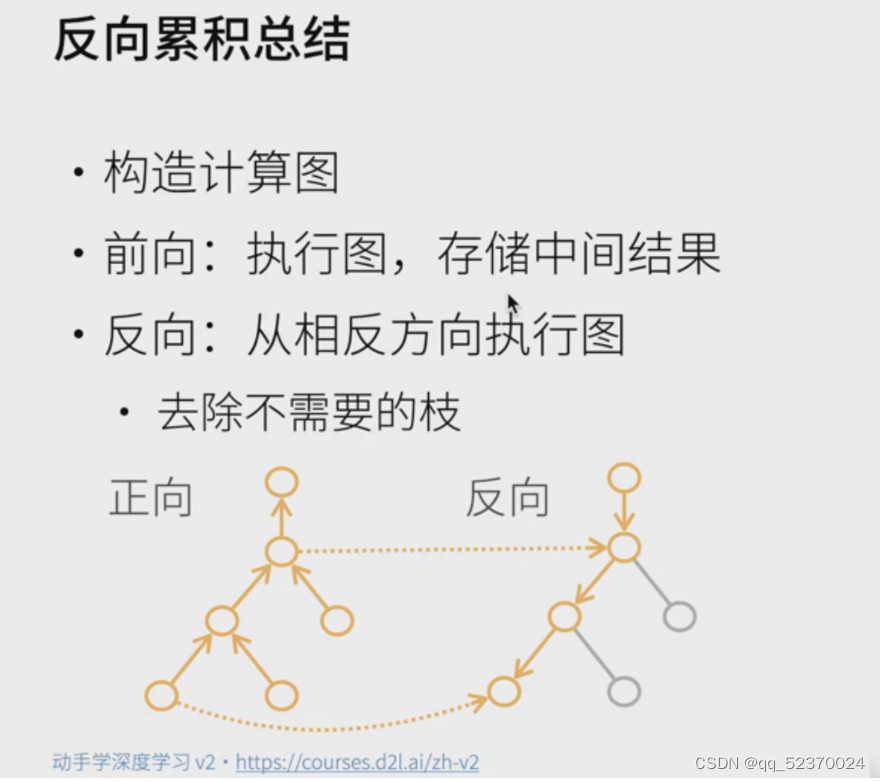
分离计算

有时，我们希望将某些计算移动到记录的计算图之外。
例如，假设y是作为x的函数计算的，而z则是作为y和x的函数计算的。
想象一下，我们想计算z关于x的梯度，但由于某种原因，希望将y视为一个常数，并且只考虑到x在y被计算后发挥的作用。

这里可以分离y来返回一个新变量u，该变量与y具有相同的值，但丢弃计算图中如何计算y的任何信息。
换句话说，梯度不会向后流经u到x。
因此，下面的反向传播函数计算z=u*x关于x的偏导数，同时将u作为常数处理，而不是z=x*x*x关于x的偏导数。

x.grad.zero_()
y = x * x
u = y.detach()
z = u * x

z.sum().backward()
x.grad == u

# tensor([True, True, True, True])

Python控制流的梯度计算

def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()

a.grad == d / a

# tensor(True)

2.6 概率

2.6. 概率 — 动手学深度学习 2.0.0 documentation

边际化

为了能进行事件概率求和，我们需要求和法则，即B的概率相当于计算A的所有可能选择，并将所有选择的联合概率聚合在一起：

$$P(B)=\sum _{A}P(A,B)$$

这也称为边际化。边际化结果的概率或分布称为边际概率（marginal probability）或边际分布。

END