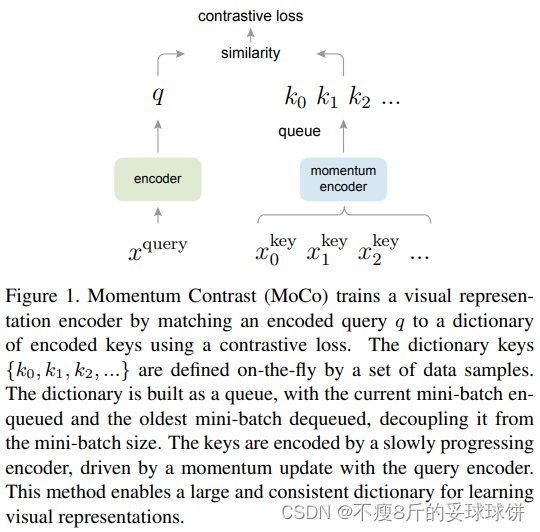
MoCo loss计算采用的损失函数是InfoNCE： ​​

下面是MoCo的伪代码，MoCo这个loss的实现就是基于cross entropy loss。

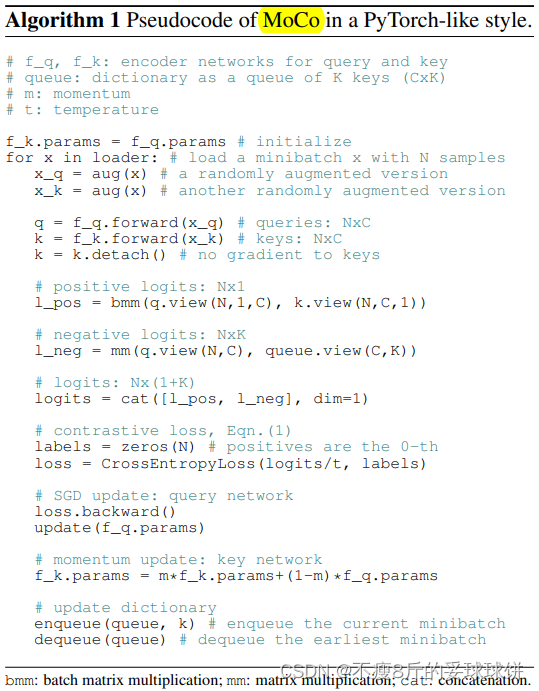
将k作为q的正样本，因为k与q是来自同一张图像的不同视图；将queue作为q的负样本，因为queue中含有大量不同图像的视图。

在具体python代码中的实现如下：

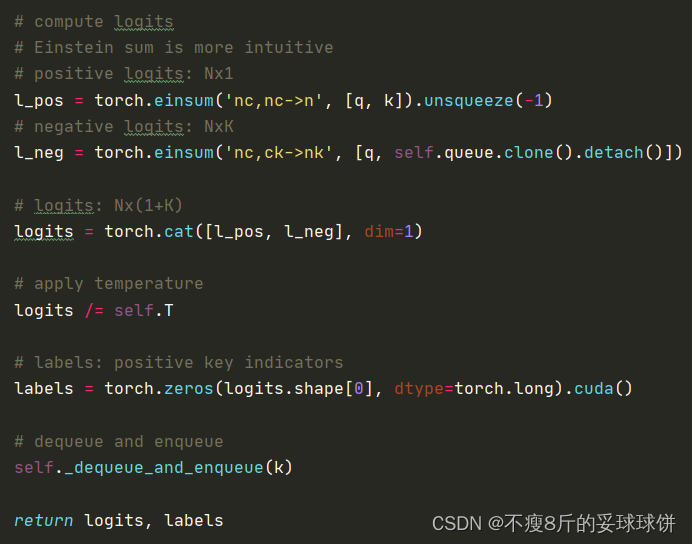
（1）首先计算正样本损失l_pos， 大小为(N, 1)。

l_pos = torch.einsum('nc,nc->n', [q, k]).unsqueeze(-1)

再计算负样本损失l_neg， 大小为(N, K)。

l_neg = torch.einsum('nc,ck->nk', [q, self.queue.clone().detach()])

（2）将l_pos和l_neg进行cat操作，并除以温度参数temperature（控制concentration level of distribution），得到logits， 大小为(N, 1+K)。

# logits: Nx(1+K)
logits = torch.cat([l_pos, l_neg], dim=1)

# apply temperature
logits /= self.T

目标是正样本都为1，负样本都为0。

（3）那么可以把logits看做分类，分成1+K个类别，期望都是第一个类别，则可以把labels设为0（为什么呢？）。

# labels: positive key indicators
labels = torch.zeros(logits.shape[0], dtype=torch.long).cuda()

（4）最后函数返回，再使用nn.CrossEntropyLoss计算损失函数。

criterion = nn.CrossEntropyLoss().cuda(args.gpu)
# ...
loss = criterion(output, target)

前面提到的可以把labels设为0（为什么呢？）

我们可以结合nn.CrossEntropyLoss详解_Lucinda6的博客-CSDN博客_nn.crossentropyloss()和https://www.cnblogs.com/marsggbo/p/10401215.html 理解一下。

交叉熵的计算公式为：

其中p表示真实值，在这个公式中是one-hot形式；q是预测值，在这里假设已经是经过softmax后的结果了。

下面详细分析一下nn.CrossEntropyLoss。

仔细观察上面的交叉熵的计算公式可以知道，因为p的元素不是0就是1，而且又是乘法，所以很自然地我们如果知道1所对应的index，那么就不用做其他无意义的运算了。所以在pytorch代码中target不是以one-hot形式表示的，而是直接用scalar表示。所以交叉熵的公式(m表示真实类别)可变形为：

仔细看看，是不是就是等同于log_softmax和nll_loss两个步骤。

所以Pytorch中的F.cross_entropy会自动调用上面介绍的log_softmax和nll_loss来计算交叉熵,其计算方式如下:

---

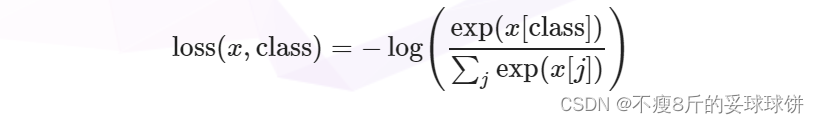
参考文章：

自监督学习MOCO算法解析 - 知乎

对比学习损失（InfoNCE loss）与交叉熵损失的联系，以及温度系数的作用 - 知乎

nn.CrossEntropyLoss详解_Lucinda6的博客-CSDN博客_nn.crossentropyloss()

https://www.cnblogs.com/marsggbo/p/10401215.html

nn.Softmax_harry_tea的博客-CSDN博客_nn.softmax

torch.einsum详解 - 知乎