题目描述
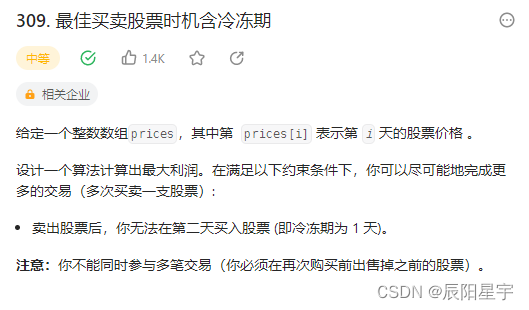


原题链接:309. 最佳买卖股票时机含冷冻期
解题思路
本次难点在于多了一个冷冻期,大体的状态过程是三个:持有股票、不持有股票、冷冻期。在不持有股票时候,又可分为之前就不持有股票并继续保持、今天才卖出股票明天是冷冻期。
(1)四种状态dp
- 动态规划五步曲:
(1)dp数组含义:
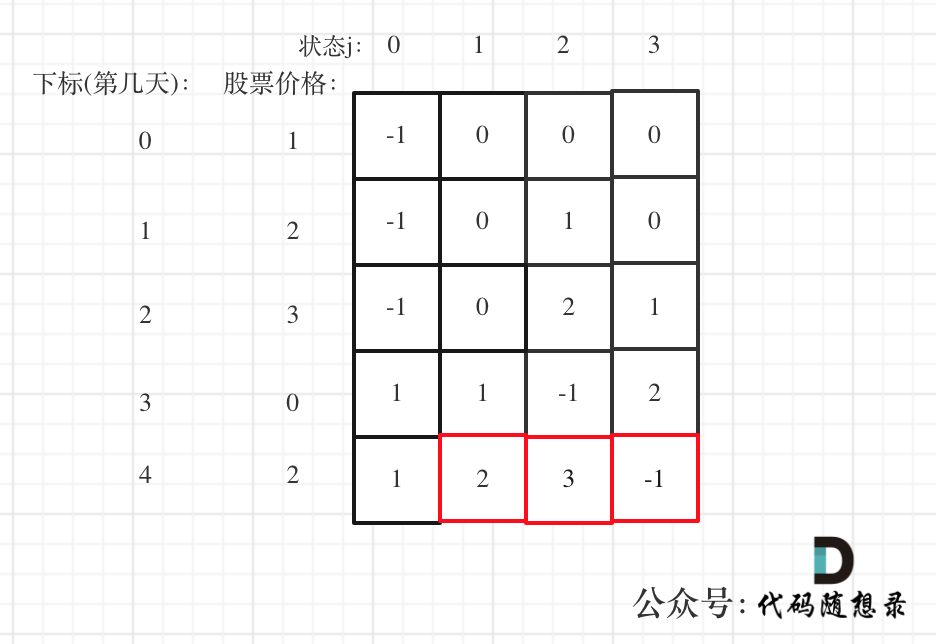
为了详细分析,分为包含四个状态,分别为:dp[i][0]:持有股票时最大收益状态、dp[i][1]:之前就不持有股票并继续保持不持有股票时的最大收益、dp[i][2]:今天才股票,明天将为冷冻期、dp[i][3]:冷冻期。
(2)递推公式:
-
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i], dp[i - 1][3] - prices[i]):取三种操作的最大值。第一种,昨天已持有并继续保持。第二种,昨天不持有并且昨天不为冷冻期,今天买入股票。第三种,昨天不持有并且昨天为冷冻期,今天买入。 -
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]):取两种操作的最大值。第一种,之前已不持有且昨天不为冷冻期,保持。第二种,之前已不持有并且昨天为冷冻期,从冷冻期转移过来。 -
dp[i][2] = dp[i - 1][0] + prices[i]:只有一种操作,今天售卖股票。 -
dp[i][3] = dp[i - 1][2]:昨天刚卖出股票,今天为冷冻期。
(3)dp数组初始化:
dp[0][0] = -prices[0],因为不能当天买当天卖dp[0][1] = dp[0][2] = dp[0][3]为非法变量,为了便于后续计算,由后续的需求可反推知,应把这三个初始化为0。
(4)遍历顺序: 从小到大。
(5)举例:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n + 1, vector<int>(4));
dp[0][0] = -prices[0];
for(int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][1] - prices[i], dp[i - 1][3] - prices[i]));
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));
}
};
参考文章:309.最佳买卖股票时机含冷冻期
(2)变量优化
dp数组和递推公式变为3个,分别为:
-
dp[i][0] = max(dp[i - 1][0], dp[i - 1][2] - prices[i]):持有股票时的最大收益,在之前的就已持有的状态和从非冷冻期后当天买入的状态中,去最大值。 -
dp[i][1] = dp[i - 1][0] + prices[i]: 今天不持有股票并且明天为冷冻期时,最大收益 -
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1]):今天不持有股票并且明天不为冷冻期时,最大收益。从之前的就已是此状态和今天才为冷冻期中选一个最大值。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n + 1, vector<int>(4));
dp[0][0] = -prices[0];
for(int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][2] - prices[i]);
dp[i][1] = dp[i - 1][0] + prices[i];
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1]);
}
return max(dp[n - 1][1], dp[n - 1][2]);
}
};
参考文章:最佳买卖股票时机含冷冻期