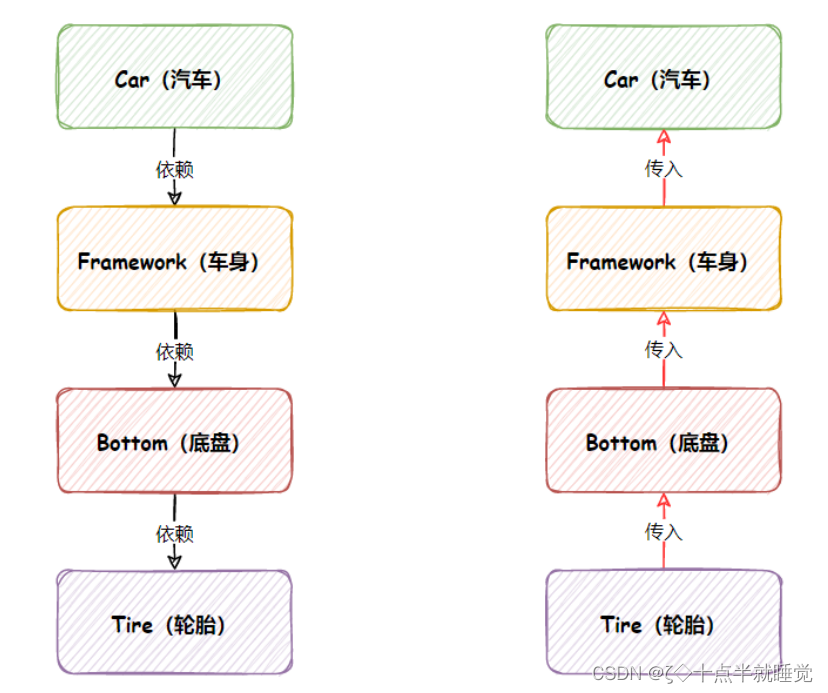
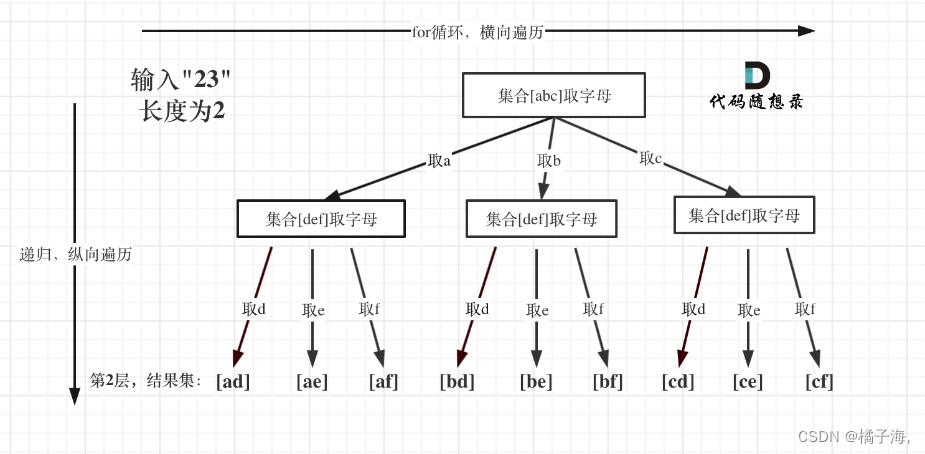
前言

这里面简单介绍一下单层感知机和多层感知机的模型

参考：

https://www.bilibili.com/video/BV17e4y1q7NG?p=41

---

一 单层感知机模型

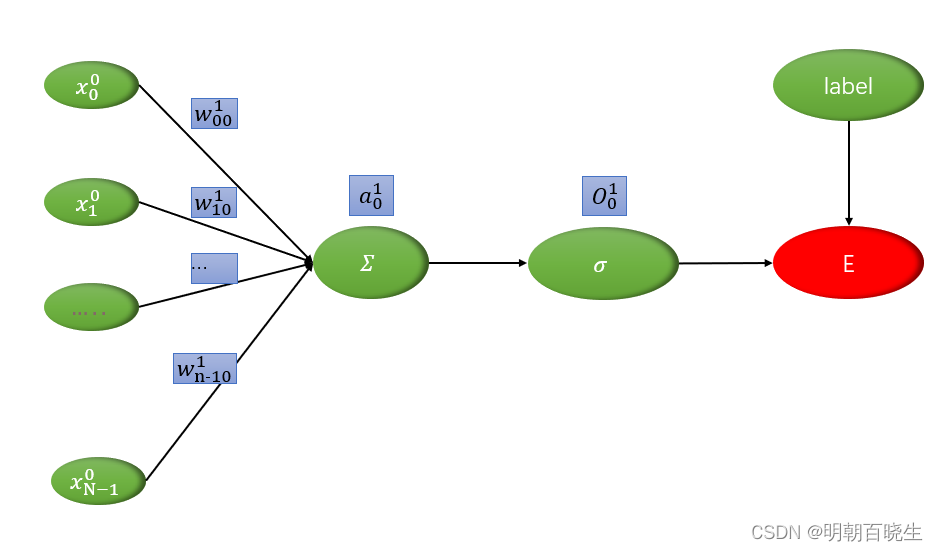
输入

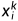: k 代表网络层数，i 代表输入节点的编号

前向传播

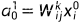
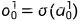
: 权重系数

k: 层数

i: 前一层输入节点编号

j: 当前层输出节点编号

这里： k=1, j =0

损失函数

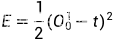
t： 标签值

Backward: 反向传播更新梯度

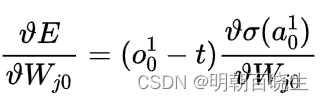
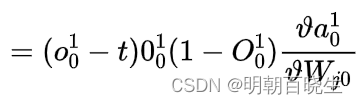
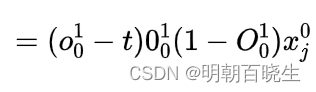
# -*- coding: utf-8 -*-
"""
Created on Fri Feb 17 16:56:58 2023

@author: chengxf2
"""

import torch
import torch.nn.functional as F

def forward(w,x):
    print("w 的梯度",w.grad)
    if w.grad is not None: 
        w.grad.data.zero_()
        print("\n 初始化的w ",w)

    a = torch.matmul(x,w.T)
    o= torch.sigmoid(a)
    
    loss = F.mse_loss(o, target)
    print("\n loss ",loss)
    return loss

def  backward(loss, w):
    
    loss.backward()
    print("\n 权重系数 ",w.data, "\n 权重系数梯度 ",w.grad,"\n 权限系数梯度", w.grad.data)
    

    
target = torch.ones(1,1) 
x = torch.randn(1,3)
w = torch.randn(1,3, requires_grad=True)
 
loss = forward(w,x)
backward(loss,w)

权重系数，以及权重系数的梯度，都是放在data 里面

---

二 多层感知机

2.1 模型

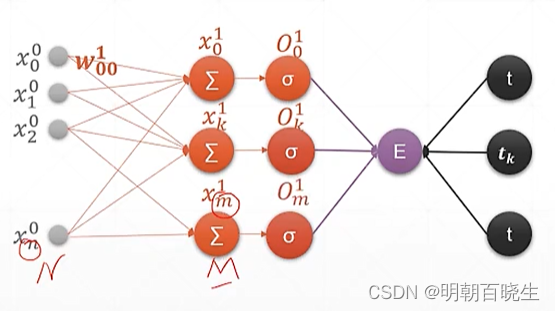
从上面可以看出梯度消失，梯度弥散的原因

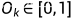
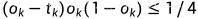
当经过多个这样的神经元梯度就会消失了

2.2 矩阵推导

另一种更普遍的方式利用矩阵方式推导

输入

Forward:

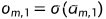
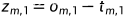
损失函数

利用迹和梯度的关系

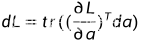
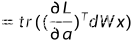
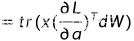
所以

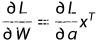
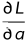利用链式求导法则

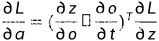
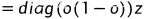
(点乘 对应 multiply)

所以

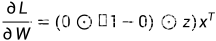
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 13 21:28:26 2023

@author: cxf
"""

import torch
import torch.nn.functional as F


def matGrad(z,o,x):
    print("\n o",o)
    a = torch.multiply(o, 1.0-o)
    print("\n a ",a)
    
    b = torch.multiply(a,z)
    
    c = torch.matmul(b,x.T)
    print("\n out \n",c/2.0)

def grad():
    
    x = torch.randn(3,1)
    w = torch.randn(4,3,requires_grad=True)
    a = torch.matmul(w, x)
    o = torch.sigmoid(a)
    
    t = torch.ones(4,1)
    
    loss = F.mse_loss(o, t)
    
    z = o-t
    matGrad(z,o,x)
    loss.backward()
    
    print("\n w grad \n ",w.grad)
    
    

if __name__ == "__main__":
    
    grad()