小波神经网络（WNN）的实现（Python，附源码及数据集）

news2024/9/20 6:14:29

文章目录

  • 一、理论基础
    • 1、小波神经网络结构
    • 2、前向传播过程
    • 3、反向传播过程
    • 4、建模步骤
  • 二、小波神经网络的实现
    • 1、训练过程（WNN.py）
    • 2、测试过程（test.py）
    • 3、测试结果
    • 4、参考源码及实验数据集

一、理论基础

小波神经网络（Wavelet Neural Network，简称WNN）是基于小波变换理论构造而成，其原理原理与反向传播神经网络（BPNN）较为接近，最主要的特征是它的隐含层神经元激活函数为小波基函数，这一特性使其充分利用了小波变换的局部化性质和神经网络的大规模数据并行处理、自学习能力，因而具有较强的逼近能力和较快的收敛速度。
反向传播神经网络（BPNN）原理参考：
反向传播神经网络（BPNN）的实现（Python，附源码及数据集）

1、小波神经网络结构

小波神经网络的结构图如下图所示：
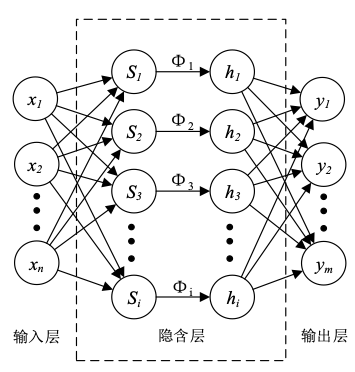
在这里插入图片描述

2、前向传播过程

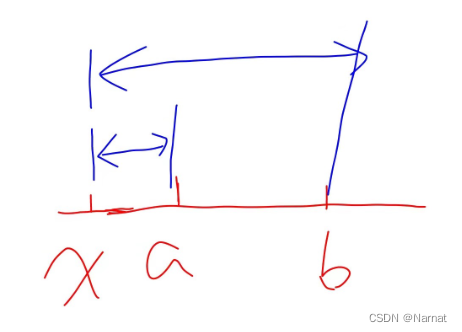
假设输入层、隐含层、输出层的节点数分别为n、i和m，则数据由输出层传递到隐含层时，隐含层第j个节点的输入数据的计算公式如下：
在这里插入图片描述

其中x_k为输入数据中第k个样本数据，ω_kj为隐含层节点的连接权值。
上述计算结果在隐含层节点处进行小波基的伸缩变化，具体的变换公式如下：
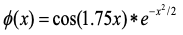
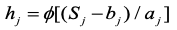
在这里插入图片描述
在这里插入图片描述

其中∅(x)为小波基函数，b_j为基函数的平滑因子，a_j为基函数的伸缩因子，h_j为隐含层第j个节点的输出数据。
最后隐含层第j个节点的输出数据进入输出层，经过计算后从输出层的t个节点输出，此节点上的计算公式如下：
在这里插入图片描述

其中ω_jt为输出层的连接权值，φ为激活函数。
激活函数原理参考：
神经网络基础知识之激活函数

3、反向传播过程

由前向传播过程可以了解到，数据在神经元与神经元之间的传递是单向的，每个神经元只接受上一层神经元传递过来的数据并对其处理。在这个处理过程中，小波神经网络主要有四个参数参与计算，这四个参数分别是小波基函数的平滑因子b_j与伸缩因子a_j以及隐含层与输出层的两个连接权值，这四个参数值的大小将直接影响网络的性能。因此WNN的训练过程如BPNN一样主要使用反向传播算法如随机梯度下降法（SGD）对这四个参数进行不断的修正。
以输出层的权值为例，其更新公式如下：
在这里插入图片描述
其中E为误差函数，μ为学习率。
损失函数原理参考：
机器学习基础知识之损失函数
反向传播原理参考：
神经网络之反向传播算法（梯度、误差反向传播算法BP）

4、建模步骤

以使用小波神经网络进行预测为例，可以将小波神经网络预测模型的建模步骤总结如下：

  1. 根据输入数据的相关特征确定小波神经网络输入层、隐含层以及输出层的节点数；
  2. 选择一种参数初始化方法对小波神经网络隐含层的连接权值、平滑因子和伸缩因子、输出层的连接权值进行随机初始化；
  3. 数据由输入层输入小波神经网络，传递至隐含层后经小波变换对数据进行非线性转换；
  4. 数据在隐含层输出后传递至输出层，在与输出层的连接权值进行线性计算后由激活函数进行非线性转换，最后得到网络的前向传播输出；
  5. 选择一种损失函数对网络的前向传播输出以及目标值进行相关计算得到损失值；
  6. 以输出层的损失值计算得到输出层连接权值以及阈值的梯度，选择一种反向传播算法对它们进行调整；
  7. 损失值传递至隐含层，同样使用相同的反向传播算法对隐含层的中心点以及宽度向量进行调整；
  8. 获得一个参数得到更新后的小波神经网络；
  9. 在达到最大迭代次数或满足停止迭代条件之前，重复步骤4到步骤8，在达到最大迭代次数后，输出所有参数确定的小波神经网络。

参数初始化方法参考：
神经网络基础知识之参数初始化

二、小波神经网络的实现

以数据预测为例，下面介绍基于Python实现小波神经网络的过程。
选用某省市的表层土壤重金属元素数据集作为实验数据，该数据集总共96组，随机选择其中的24组作为测试数据集，72组作为训练数据集。选取重金属Ti的含量作为待预测的输出特征，选取重金属Co、Cr、Mg、Pb作为模型的输入特征。

1、训练过程（WNN.py）

#库的导入
import numpy as np
import pandas as pd
import math

#激活函数
def tanh(x):
    return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
#激活函数偏导数
def de_tanh(x):
    return (1-x**2)
#小波基函数
def wavelet(x):
    return (math.cos(1.75*x)) * (np.exp((x**2)/(-2)))
#小波基函数偏导数
def de_wavelet(x):
    y = (-1) * (1.75 * math.sin(1.75 * x)  + x * math.cos(1.75 * x)) * (np.exp(( x **2)/(-2)))
    return y

#参数设置
samnum = 72   #输入数据数量
hiddenunitnum = 8   #隐含层节点数
indim = 4   #输入层节点数
outdim = 1   #输出层节点数
maxepochs = 500   #迭代次数
errorfinal = 0.65*10**(-3)   #停止迭代训练条件
learnrate = 0.001   #学习率


#输入数据的导入
df = pd.read_csv("train.csv")
df.columns = ["Co", "Cr", "Mg", "Pb", "Ti"]
Co = df["Co"]
Co = np.array(Co)
Cr = df["Cr"]
Cr = np.array(Cr)
Mg=df["Mg"]
Mg=np.array(Mg)
Pb = df["Pb"]
Pb =np.array(Pb)
Ti = df["Ti"]
Ti = np.array(Ti)
samplein = np.mat([Co,Cr,Mg,Pb])
#数据归一化，将输入数据压缩至0到1之间，便于计算，后续通过反归一化恢复原始值
sampleinminmax = np.array([samplein.min(axis=1).T.tolist()[0],samplein.max(axis=1).T.tolist()[0]]).transpose()#对应最大值最小值
#待预测数据为Ti
sampleout = np.mat([Ti])
sampleoutminmax = np.array([sampleout.min(axis=1).T.tolist()[0],sampleout.max(axis=1).T.tolist()[0]]).transpose()#对应最大值最小值
sampleinnorm = ((np.array(samplein.T)-sampleinminmax.transpose()[0])/(sampleinminmax.transpose()[1]-sampleinminmax.transpose()[0])).transpose()
sampleoutnorm = ((np.array(sampleout.T)-sampleoutminmax.transpose()[0])/(sampleoutminmax.transpose()[1]-sampleoutminmax.transpose()[0])).transpose()

#给归一化后的数据添加噪声
noise = 0.03*np.random.rand(sampleoutnorm.shape[0],sampleoutnorm.shape[1])
sampleoutnorm += noise

#
scale = np.sqrt(3/((indim+outdim)*0.5))
w1 = np.random.uniform(low=-scale,high=scale,size=[hiddenunitnum,indim])
b = np.random.uniform(low=-scale, high=scale, size=[hiddenunitnum,1])
a = np.random.uniform(low=-scale, high=scale, size=[hiddenunitnum,1])
w2 = np.random.uniform(low=-scale,high=scale,size=[hiddenunitnum,outdim])

#对隐含层的连接权值w1、平滑因子被b和伸缩因子a、输出层的连接权值w2进行随机初始化
inputin=np.mat(sampleinnorm.T)
w1=np.mat(w1)
b=np.mat(b)
a=np.mat(a)
w2=np.mat(w2)

#errhistory存储每次迭代训练计算的误差
errhistory = np.mat(np.zeros((1,maxepochs)))
#开始训练
for i in range(maxepochs):
    #前向计算：
    #hidden_out为隐含层输出
    hidden_out = np.mat(np.zeros((samnum,hiddenunitnum)))
    for m in range(samnum):
        for j in range(hiddenunitnum):
            d=((inputin[m, :] * w1[j, :].T) - b[j,:]) * (a[j,:] ** (-1))
            hidden_out[m,j] = wavelet(d)
    #output为输出层输出
    output = tanh(hidden_out * w2)
    #计算误差
    out_real = np.mat(sampleoutnorm.transpose())
    err = out_real - output
    loss = np.sum(np.square(err))
    #判断是否停止训练
    if loss < errorfinal:
        break
    errhistory[:,i] = loss
    #反向计算
    out_put=np.array(output.T)
    belta=de_tanh(out_put).transpose()
    #分别计算每个参数的误差项
    for j in range(hiddenunitnum):
        sum1 = 0.0
        sum2 = 0.0
        sum3 = 0.0
        sum4 = 0.0
        sum5 = 0.0
        for m in range(samnum):
            sum1+= err[m,:] * belta[m,:] * w2[j,:] * de_wavelet(hidden_out[m,j]) * (inputin[m,:] / a[j,:])
            #1*1
            sum2+= err[m,:] * belta[m,:] * w2[j,:] * de_wavelet(hidden_out[m,j]) * (-1) * (1 / a[j,:])
            #1*1
            sum3+= err[m,:] * belta[m,:] * w2[j,:] * de_wavelet(hidden_out[m,j]) * (-1) * ((inputin[m,:] * w1[j,:].T - b[j,:]) / (a[j,:] * a[j,:]))
            #1*1
            sum4+= err[m,:] * belta[m,:] * hidden_out[m,j]
        delta_w1 = sum1
        delta_b = sum2
        delta_a = sum3
        delta_w2 = sum4
        #根据误差项对四个参数进行更新
        w1[j,:] = w1[j,:] + learnrate * delta_w1
        b[j,:] = b[j,:] + learnrate * delta_b
        a[j,:] = a[j,:] + learnrate * delta_a
        w2[j,:] = w2[j,:] + learnrate * delta_w2
    print("the generation is:",i+1,",the loss is:",loss)

print('更新的w1:',w1)
print('更新的b:',b)
print('更新的w2:',w2)
print('更新的a:',a)
print("The loss after iteration is ：",loss)

np.save("w1.npy",w1)
np.save("b.npy",b)
np.save("w2.npy",w2)
np.save("a.npy",a)

2、测试过程（test.py）

#库的导入
import numpy as np
import pandas as pd
import math

#小波基函数
def wavelet(x):
    return (math.cos(1.75*x)) * (np.exp((x**2)/(-2)))
#激活函数tanh
def tanh(x):
    return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))


#输入数据的导入，用于测试数据的归一化与返归一化
df = pd.read_csv("train.csv")
df.columns = ["Co", "Cr", "Mg", "Pb", "Ti"]
Co = df["Co"]
Co = np.array(Co)
Cr = df["Cr"]
Cr = np.array(Cr)
Mg=df["Mg"]
Mg=np.array(Mg)
Pb = df["Pb"]
Pb =np.array(Pb)
Ti = df["Ti"]
Ti = np.array(Ti)
samplein = np.mat([Co,Cr,Mg,Pb])
sampleinminmax = np.array([samplein.min(axis=1).T.tolist()[0],samplein.max(axis=1).T.tolist()[0]]).transpose()#对应最大值最小值
sampleout = np.mat([Ti])
sampleoutminmax = np.array([sampleout.min(axis=1).T.tolist()[0],sampleout.max(axis=1).T.tolist()[0]]).transpose()#对应最大值最小值

#导入WNN.py训练好的参数
w1=np.load('w1.npy')
b=np.load('b.npy')
a=np.load('a.npy')
w2=np.load('w2.npy')
w1 = np.mat(w1)
w2 = np.mat(w2)
b = np.mat(b)
a = np.mat(a)

#隐含层节点数
hiddenunitnum = 8
#测试数据数量
testnum = 24


#测试数据的导入
df = pd.read_csv("test.csv")
df.columns = ["Co", "Cr", "Mg", "Pb", "Ti"]
Co = df["Co"]
Co = np.array(Co)
Cr = df["Cr"]
Cr = np.array(Cr)
Mg=df["Mg"]
Mg=np.array(Mg)
Pb = df["Pb"]
Pb =np.array(Pb)
Ti = df["Ti"]
Ti = np.array(Ti)
input=np.mat([Co,Cr,Mg,Pb])

#测试数据中输入数据的归一化
inputnorm=(np.array(input.T)-sampleinminmax.transpose()[0])/(sampleinminmax.transpose()[1]-sampleinminmax.transpose()[0])
#hidden_out2用于保存隐含层输出
hidden_out = np.mat(np.zeros((testnum,hiddenunitnum)))
#计算隐含层输出
for m in range(testnum):
    for j in range(hiddenunitnum):
        d = ((inputnorm[m, :] * w1[j, :].T) - b[j, :]) * (a[j, :] ** (-1))
        hidden_out[m, j] = wavelet(d)
#计算输出层输出
output = tanh(hidden_out * w2 )
#对输出结果进行反归一化
diff = sampleoutminmax[:,1]-sampleoutminmax[:,0]
networkout2 = output*diff+sampleoutminmax[0][0]
networkout2 = np.array(networkout2).transpose()
output1=networkout2.flatten()#降成一维数组
output1=output1.tolist()
for i in range(testnum):
    output1[i] = float('%.2f'%output1[i])
print("the prediction is:",output1)

#将输出结果与真实值进行对比，计算误差
output=Ti
rmse = (np.sum(np.square(output-output1))/len(output)) ** 0.5
mae = np.sum(np.abs(output-output1))/len(output)
average_loss1=np.sum(np.abs((output-output1)/output))/len(output)
mape="%.2f%%"%(average_loss1*100)
f1 = 0
for m in range(testnum):
    f1 = f1 + np.abs(output[m]-output1[m])/((np.abs(output[m])+np.abs(output1[m]))/2)
f2 = f1 / testnum
smape="%.2f%%"%(f2*100)
print("the MAE is :",mae)
print("the RMSE is :",rmse)
print("the MAPE is :",mape)
print("the SMAPE is :",smape)

#计算预测值与真实值误差与真实值之比的分布
A=0
B=0
C=0
D=0
E=0
for m in range(testnum):
    y1 = np.abs(output[m]-output1[m])/np.abs(output[m])
    if y1 <= 0.1:
        A = A + 1
    elif y1 > 0.1 and y1 <= 0.2:
        B = B + 1
    elif y1 > 0.2 and y1 <= 0.3:
        C = C + 1
    elif y1 > 0.3 and y1 <= 0.4:
        D = D + 1
    else:
        E = E + 1
print("Ratio <= 0.1 :",A)
print("0.1< Ratio <= 0.2 :",B)
print("0.2< Ratio <= 0.3 :",C)
print("0.3< Ratio <= 0.4 :",D)
print("Ratio > 0.4 :",E)

3、测试结果

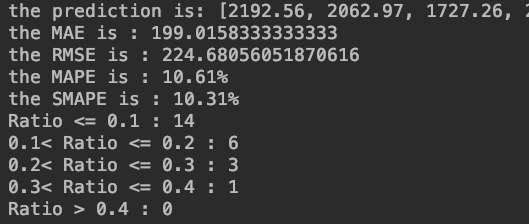
在这里插入图片描述
注：由于每次初始化生成的参数不同，因此对参数设置相同的神经网络进行多次训练和预测，测试结果不会完全一致，此外测试结果的好坏也会受到隐含层节点数、学习率、训练次数等参数的影响。

4、参考源码及实验数据集

参考源码及实验数据集

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/358936.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Python实现性能自动化测试，还可以如此简单

Python实现性能自动化测试，还可以如此简单

Python实现性能自动化测试&#xff0c;还可以如此简单 目录&#xff1a;导读 一、思考❓❔ 二、基础操作&#x1f528;&#x1f528; 三、综合案例演练&#x1f528;&#x1f528; 四、总结&#x1f4a1;&#x1f4a1; 写在最后 一、思考❓❔ 1.什么是性能自动化测试? 性…
阅读更多...
宁盾上榜第五版《CCSIP 2022 中国网络安全行业全景册》

宁盾上榜第五版《CCSIP 2022 中国网络安全行业全景册》

2月1日&#xff0c;国内网络安全行业媒体Freebuf咨询正式发布《CCSIP&#xff08;China Cyber Security Panorama&#xff09;2022 中国网络安全行业全景册》第五版。宁盾作为国产身份安全厂商入驻身份识别和访问管理&#xff08;SSO、OTP、IDaaS&#xff09;及边界访问控制&am…
阅读更多...
Unity毛发系统TressFX Exporter

Unity毛发系统TressFX Exporter

Unity 数字人交流群&#xff1a;296041238 一&#xff1a;在Maya下的TressFX Exporter 插件安装步骤&#xff1a; 1. 下载Maya的TressFX Exporter插件 下载地址&#xff1a;TressFX Exporter 链接&#xff1a;https://github.com/Unity-China/cn.unity.hairfx.core/tree/m…
阅读更多...
货仓选址 AcWing（JAVA）

货仓选址 AcWing（JAVA）

在一条数轴上有 N家商店&#xff0c;它们的坐标分别为 A1∼AN。 现在需要在数轴上建立一家货仓&#xff0c;每天清晨&#xff0c;从货仓到每家商店都要运送商品。 为了提高效率&#xff0c;求把货仓建在何处&#xff0c;可以使得货仓到每家商店的距离之和最小。 输入格式&#…
阅读更多...
Spring Cloud Alibaba--ActiveMQ微服务详解之消息队列（四）

Spring Cloud Alibaba--ActiveMQ微服务详解之消息队列（四）

上篇讲述高并发情况下的数据库处理方式&#xff1a;分布式事务管理机制。即使我们做到这一步并发情况只能稍微得到缓解&#xff0c;当然千万级别的问题不大&#xff0c;但在面对双十一淘宝这类的达上亿的并发的时候仅仅靠分布式事务管理还是远远不够&#xff0c;即使数据库可以…
阅读更多...
基于Django和vue的微博用户情感分析系统

基于Django和vue的微博用户情感分析系统

完整代码&#xff1a;https://download.csdn.net/download/weixin_55771290/87471350概述这里简单说明一下项目下下来直接跑起的方法。前提先搞好python环境和vue环境,保证你有一个账户密码连上数据库mysql。1、pip install requirements.txt 安装python包2、修改mysql数据库的…
阅读更多...
Hadoop HDFS的主要架构与读写文件

Hadoop HDFS的主要架构与读写文件

一、Hadoop HDFS的架构 HDFS&#xff1a;Hadoop Distributed File System&#xff0c;分布式文件系统 &#xff11;&#xff0c;NameNode 存储文件的metadata&#xff0c;运行时所有数据都保存到内存&#xff0c;整个HDFS可存储的文件数受限于NameNode的内存大小一个Block在…
阅读更多...
使用物联网进行智能能源管理的10大优势

使用物联网进行智能能源管理的10大优势

如今&#xff0c;物联网推动了许多行业的自动化流程和运营效率&#xff0c;而物联网在能源领域的应用尤其受到消费者、企业甚至政府的关注。除了对电力供应链的诸多好处之外&#xff0c;物联网能源管理系统还让位于新的智能电网&#xff0c;并有望实现更高的安全性和效率。基于…
阅读更多...
软件架构知识6-高性能数据库集群：读写分离

软件架构知识6-高性能数据库集群：读写分离

一、读写分离 读写分离原理&#xff1a;将数据库读写操作分散到不同的节点上&#xff1a; 读写分离的基本实现是&#xff1a; 1、数据库服务器搭建主从集群&#xff0c;一主一从&#xff0c;一主多从都可以&#xff1b; 2、数据库主机负责读写操作&#xff0c;从机只负责读操…
阅读更多...
【2023-02-20】JS逆向之翼支付

【2023-02-20】JS逆向之翼支付

提示&#xff1a;文章仅供参考&#xff0c;禁止用于非法途径 文章目录前言分析总结前言 真的好久没更了…… 提示&#xff1a;以下是本篇文章正文内容&#xff0c;下面案例可供参考 分析 进到网页&#xff0c;加载两个接口 applyLoginFactor 接口返回一个RSA公钥&#xff0…
阅读更多...
vulnhub zico2

vulnhub zico2

总结&#xff1a;脏牛提权 目录 下载地址 漏洞分析 信息收集 木马上传 反弹shell 提权 下载地址 zico2.ova (Size: 828 MB)Download: https://www.dropbox.com/s/dhidaehguuhyv9a/zico2.ovaDownload (Mirror): https://download.vulnhub.com/zico/zico2.ova使用方法&…
阅读更多...
机智的Open3D学习生活（第一集）：入坑前的准备工作

机智的Open3D学习生活（第一集）：入坑前的准备工作

1、Open3D的开源项目地址&#xff1a; https://github.com/isl-org/Open3D 2、Open3D的官网地址&#xff1a; http://www.open3d.org/ 3、Open3D的文档地址&#xff1a;http://www.open3d.org/docs/latest/tutorial/visualization/cpu_rendering.html 后续我将以此文档作为蓝…
阅读更多...
如何单独清除某个网页的缓存（reload）

如何单独清除某个网页的缓存（reload）

有时候在自己服务器上调试的时候&#xff0c;刷新一直不更新&#xff0c;样式改了也看不到&#xff0c;就很烦 今天教你一个方法快速清除 F12 控制台情况下右击左上角的刷新 这三个分别代表&#xff1a; ①正常重新加载(Ctrl R): 正常重新加载 此方法,浏览器发送请求时会…
阅读更多...
深入Spring底层透析Bean创建过程之拨云见日篇

深入Spring底层透析Bean创建过程之拨云见日篇

目录前言一.BeanFactory快速入门1. BeanFactory创建Bean2. BeanFactory和ApplicationContext的关系3. 和ApplicationContext区别(高频问点)4. BeanFactory的继承体系5. ApplicationContext的继承体系二.Bean实例化的基本流程&#xff08;重点)前言 首先感谢您的阅览&#xff0…
阅读更多...
Git复习

Git复习

1. 引言 现在要用到Git&#xff0c;复习一下关于Git的指令&#xff0c;知识摘自《Pro Git》 2. 起步 git和其他版本控制软件最大的差别在于git是直接记录某个版本的快照&#xff0c;而不是逐渐地比较差异。 安装: sudo apt install git-all设置用户信息&#xff1a; git c…
阅读更多...
上海亚商投顾：沪指放量大涨 券商等权重板块全线飙升

上海亚商投顾：沪指放量大涨 券商等权重板块全线飙升

上海亚商投顾前言&#xff1a;无惧大盘涨跌&#xff0c;解密龙虎榜资金&#xff0c;跟踪一线游资和机构资金动向&#xff0c;识别短期热点和强势个股。市场情绪三大指数今日集体反弹&#xff0c;沪指、深成指单边拉升&#xff0c;午后均涨超2%&#xff0c;上证50大涨超2.7%&…
阅读更多...
加入CSDN的一年，我收获了这些……

加入CSDN的一年，我收获了这些……

加入CSDN的一年&#xff0c;我收获了这些……加入CSDN的一年&#xff0c;我收获了这些……加入CSDN的一年&#xff0c;我收获了这些…… &#x1f680;&#x1f680;时光如白驹过隙般&#xff0c;飞逝而过。一转眼&#xff0c;我就已经是一名大二的学生了&#xff0c;也已经在…
阅读更多...
LeetCode 每日一题2347. 最好的扑克手牌

LeetCode 每日一题2347. 最好的扑克手牌

Halo&#xff0c;这里是Ppeua。平时主要更新C语言&#xff0c;C&#xff0c;数据结构算法......感兴趣就关注我吧&#xff01;你定不会失望。 &#x1f308;个人主页&#xff1a;主页链接 &#x1f308;算法专栏&#xff1a;专栏链接 我会一直往里填充内容哒&#xff01; &…
阅读更多...
Homekit智能家居一智能灯泡

Homekit智能家居一智能灯泡

一、什么是智能灯 传统的灯泡是通过手动打开和关闭开关来工作。有时&#xff0c;它们可以通过声控、触控、红外等方式进行控制&#xff0c;或者带有调光开关&#xff0c;让用户调暗或调亮灯光。 智能灯泡内置有芯片和通信模块&#xff0c;可与手机、家庭智能助手、或其他智能…
阅读更多...
网络高可用方案

网络高可用方案

目录 1. 网络高可用 2. 高可用方案设计 2.1 方案一 堆叠 ha负载均衡模式 2.2 方案二 OSPF ha负载均衡模式 3. 高可用保障 1. 网络高可用 网络高可用&#xff0c;是指对于网络的核心部分或设备在设计上考虑冗余和备份&#xff0c;减少单点故障对整个网络的影响。其设计应…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023