【NLP】一种联合关系抽取模型—

【NLP】一种联合关系抽取模型——TPLinker

news2024/12/26 9:23:45

背景

前文介绍了【NLP】一种基于联合方式的三元组抽取模型——CasRel.这个模型虽然实体和关系同时训练，但本质上来说还是分阶段的预测实体和关系，依然存在暴露偏差问题。下面介绍一个解决暴露偏差的模型：TPLinker，论文地址：TPLinker: Single-stage Joint Extraction of Entities and Relations Through Token Pair Linking,有兴趣的可以看一下原文。论文对应的源码地址：https://github.com/131250208/TPlinker-joint-extraction.

TPLinker，其中的T，P分别表示Token Pair，Linker就是Token之间的连接器，后文我们可以看到巧妙的模型设计。该模型不仅可以解决暴露偏差，还能够抽取overlap Entity，seo，epo问题也是可以解决的。整体效果也算不错的。

该模型的核心包含两个模块：1.handshaking tagging schema,2. decoding algorithm。

Handshaking Tagging Schema

Tagging

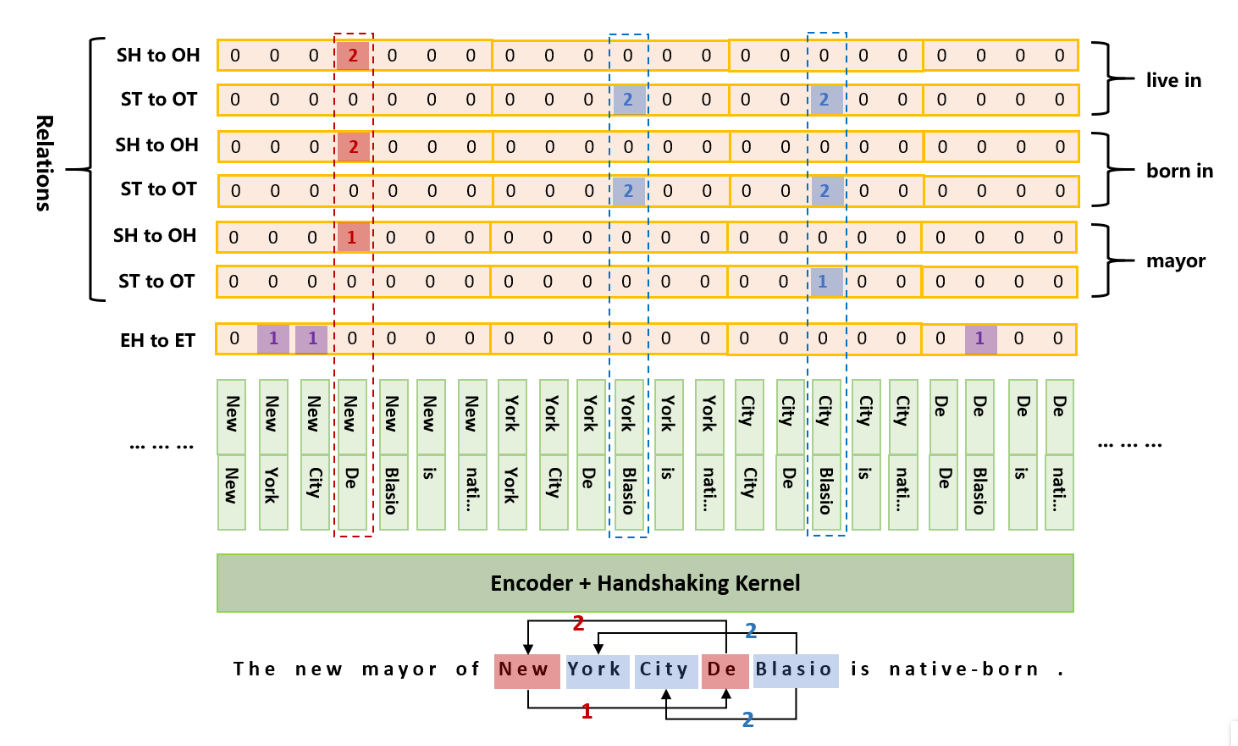
使用一个二维矩阵表示一个句子，句子中的所有token pair就可以表达了。如下图中的左边的那部分。

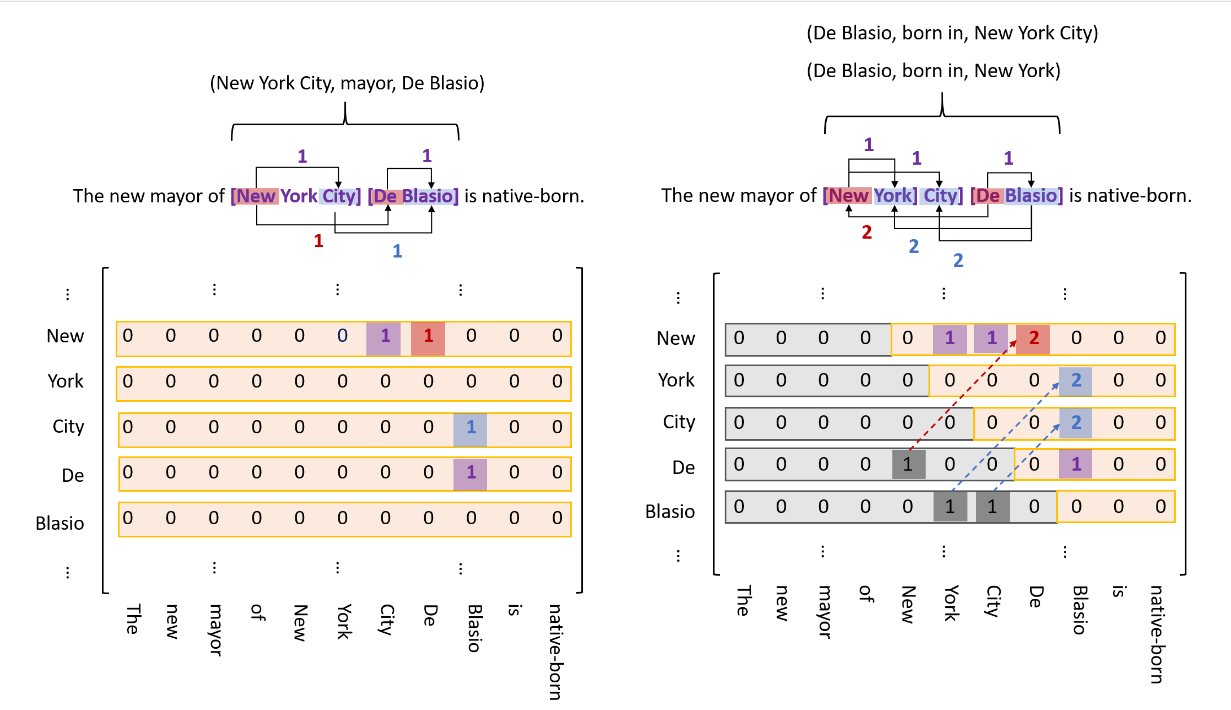
在这里插入图片描述
文中设计的token pair linker有如下三种：

一个实体的头token与尾token之间的link，entity head to entity tail（EH-to-ET），上图中 New York是一个实体，该实体就可以在纵坐标为New，横坐标为York对应的索引位置标注为1即可表示为一个实体，即头，尾中的span内容就是一个实体；
subject 实体的head指向object实体的head之间的link，subject head to object head（SH-to-OH），例如New York 的 New 与 De Blasio中的De，就构成了一个token pair；
subject 实体的tail指向object实体的tail之间的link，subject tail to object tail（ST-to-OT），例如上图中的（“City”, “Blasio”）

从上图中的左半部分可以看出，这个矩阵是非常稀疏的，特别是下三角区域，因为一个实体的尾部不可能出现在实体头部之前，那么对应的token pair linker就不可能出现在下三角的区域中，这也会造成巨大的内存消耗。但是在关系中，object实体可能会出现在subject之前，也就是说下三角区域可能存在object在subject之前的token pair linker，那么下三角的那部分也不能给直接干掉了。文中采取的方式是将下三角中的tag 1映射到上三角中对应位置，设置标签为tag 2。（如何overlap实体之间存在关系的话，那么对应位置应该是多标签的，带着这个问题往下看）。映射完毕之后，就可以把剩余的部分做展平处理，用一个map记录原矩阵中的位置信息。一个处理案例如下：

在这里插入图片描述
对于刚才那个问题（本质上来说就是解决EPO问题），即不同的关系不能标记到同一矩阵中，也不能与实体重复。为了解决这个问题，该模型为每个关系执行相同的矩阵标记工作。那么就相当于构建一个2N+1个sequence labeling 子任务，N表示预定义关系数据，每个子任务有构建了一个长为 $\frac{n^2+n}{2}$ （包含对角线的上三角tag数量），n表示输入语句的长度。其中数据的计算量也会随着序列长度的增加呈平方形式的增加。当然，encoder被所有的tagger所共享，只需要一次性构建所有的token就够用了，整体还是有不错的效果。

Decoding

继续看一下第二张图，（“New”, “York”）、（“New”,“City”）、（“De”,“Blasio”）在EH-to-ET序列中分别表示着New York,New York City,De Blasio这三个实体。

对于关系mayor（New， De）在SH-to-OH序列中被标记为1，其表示subject 以 New 开始，object以De开始，（City，Blasio）在ST-to-OT 序列中被标记为1，表示subject和object分别以City、Blasio结尾。那么对应的解码结果就是（New York City，mayor，De Blasio）。同理其他的关系也是使用这种关系进行解码。

需要注意的是tag 2与tag 1表示的意义相反。例如：（York，Blasio）在born in类别中的ST-to-OT序列中被标记为2，其代表的意义是York，Blasio分别代表的是object和subject实体的尾token，对应解码后的结果是：（De Blasio，born in， New York）。对应的解码算法如下：

在这里插入图片描述

Token Pair Representation

token pair如何进行表征呢？给定一个长度为n的语句 $[w_1, \cdots, w_n]$ ，首先将每个token $w_i$ 使用一个基本的编码器，如bert，lstm等转换成一个低纬度结合上下文向量 $h_i$ 。对于一个token pair（w_i, w_j）我们可以生成一个特征表示 $h_{i,j}$ ，如下：

$h_{i,j} = tanh(W_h\cdot[h_i;h_j] + b_h)，j\ge i$
通常：[]中的向量是使用拼接的方式，当然可以使用其他方式如平均等。 $W_h$ 是一个参数矩阵， $b_h$ 是一个bias向量，都是在训练过程中需要学习的。上式也是Handshaking Kernel的数学表示。

Handshaking Tagger

对于给定的token pair 的表示 $h_{i, j}$ ，那么token pair $w_i, w_j)$ link的标签可使用如下公式进行预测：

$P(y_{i,j}) = Softmax(W_o\cdot_{i, j} + b_o)$

$link(w_i, w_j) = \underset{l}{\arg\max}P(y_{i, j}=l)$
其中 $P(y_{i,j}=l)$ 表示token pair $w_i, w_j)$ link识别的标签为l的概率。

loss function

那么模型的损失函数该如何构建呢？具体如下：
$L_{l i n k}=-\frac{1}{N} \sum_{i=1, j \geq i}^N \sum_{* \in\{E, H, T\}} \log P\left(y_{i, j}^*=\hat{l}^*\right)$
其中， $N$ 表示输入序列的长度， $\hat{l}$ 表示正确的tag， $E, H, T$ 分别表示EH-to-ET，SH-to-OH和ST-to-OT的tagger。