- 前置知识1:矩阵范数
- 前置知识2:舒尔补
- 前置知识3:可约矩阵
- 前置知识4:谱半径
- 1.【线性方程组】直接求解:高斯消元法( L U LU LU分解)、 L D V LDV LDV分解、 L D L T LDL^T LDLT分解、 U D U T UDU^T UDUT分解
- 2. 【线性方程组】间接迭代求解:Jacobi方法, Gauss-Seidel方法
- 2.1 Jacobi方法
- 2.2 Gauss-Seidel方法
- 2.3 Jacobi方法, Gauss-Seidel方法收敛的条件
- 2.4 预测迭代次数
- 2.5 连续超松弛方法(The Method of Successive Over-Relaxation【SOR】)
- 2.6 总结:Jacobi方法, Gauss-Seidel方法对比:
- 2.7 对称矩阵的Gauss-Seidel方法
- 2.8 Krylov方法(Krylov methods)
- 2.9 GMRES方法(Generalized Minimum Residual Method)
- 3. 【线性方程组】基于优化的方法
- 3.1 共轭梯度法(Conjugate gradient method【CG】)
- 3.2 共轭梯度法和其他算法的对比
- 3.3 预条件共轭梯度法(Preconditioned conjugate gradient method)
- 4. 【非线性方程组】Jacobian矩阵、Newton迭代法、不动点迭代法、Seidel迭代法
- 4.1 Jacobian矩阵
- 4.2 Newton迭代法
- 4.3 不动点迭代法
- 4.4 Seidel迭代法
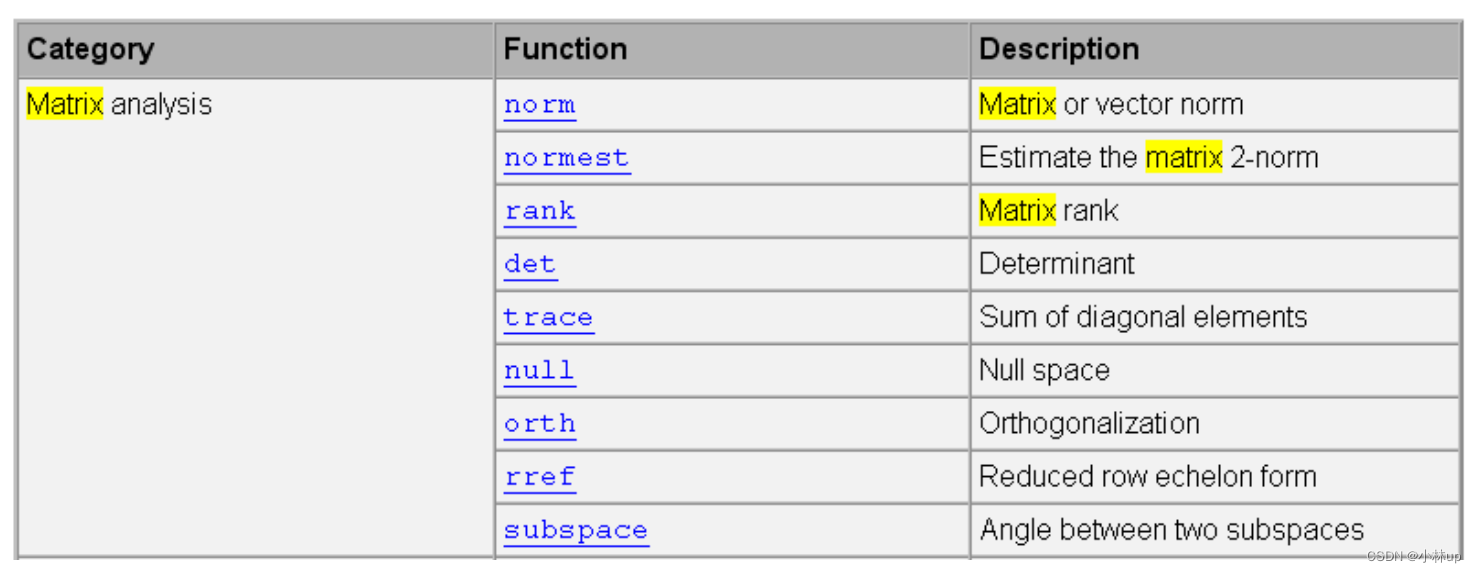
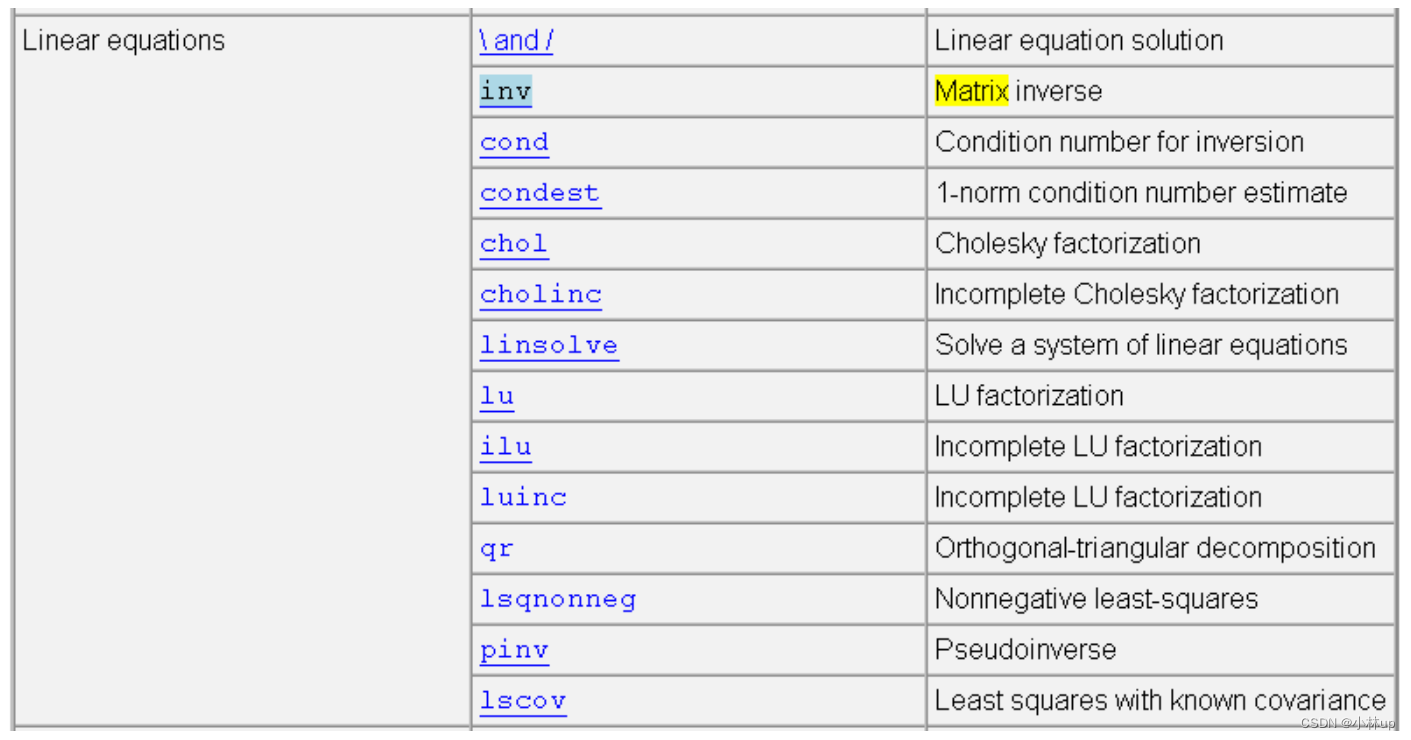
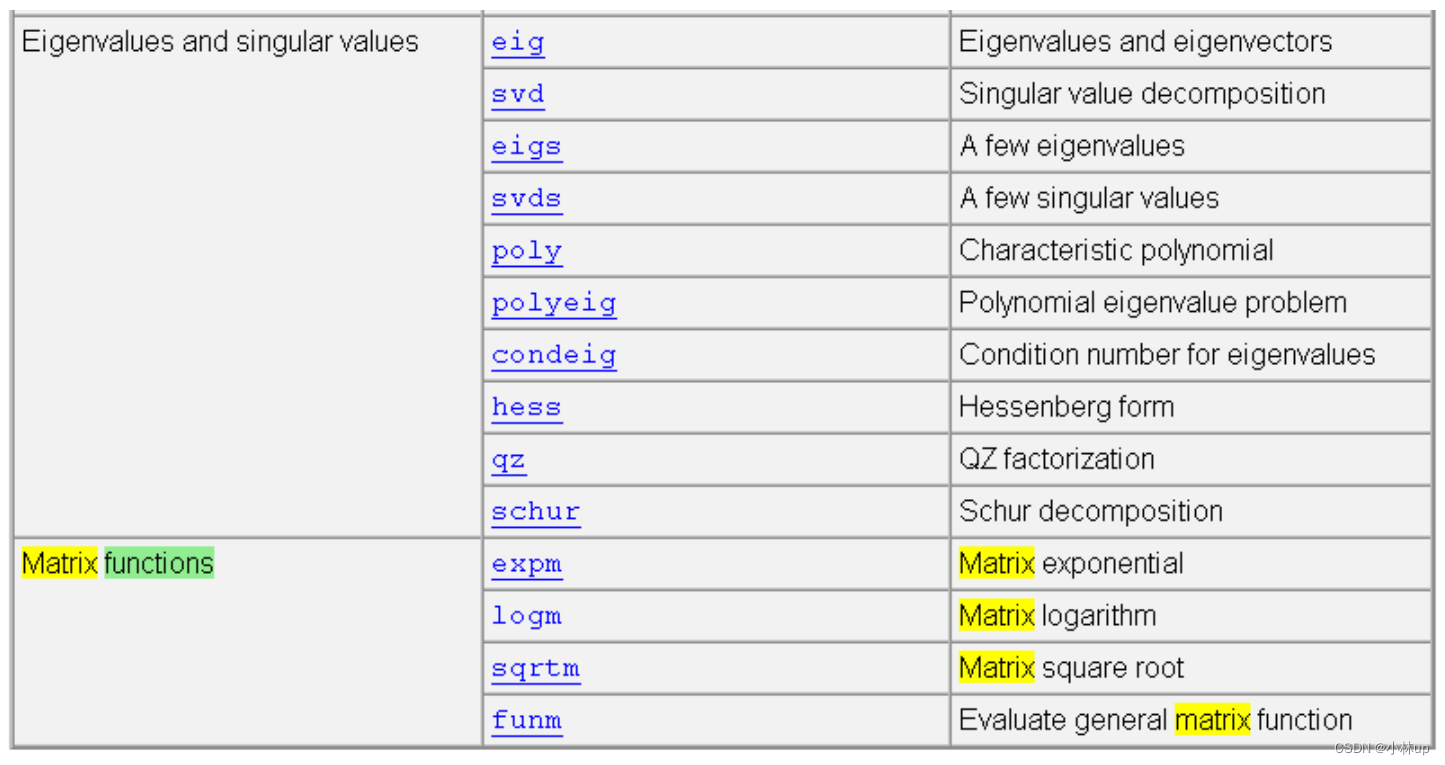
- 5. Matlab相关函数
前置知识1:矩阵范数
矩阵范数的性质:
(1) 若
A
≠
0
A \neq 0
A=0 , 那么
∥
A
∥
>
0
\|A\|>0
∥A∥>0; 若
A
=
0
A=0
A=0 , 那么
∥
A
∥
=
0
\|A\|=0
∥A∥=0 .
(2) 对于
α
∈
R
\alpha \in \mathrm{R}
α∈R,
∥
α
A
∥
=
∣
α
∣
∥
A
∥
\|\alpha A\|=|\alpha|\|A\|
∥αA∥=∣α∣∥A∥ .
(3)
∥
A
+
B
∥
≤
∥
A
∥
+
∥
B
∥
\|A+B\| \leq\|A\|+\|B\|
∥A+B∥≤∥A∥+∥B∥.
(4)
∥
A
B
∥
≤
∥
A
∥
∥
B
∥
\|A B\| \leq\|A\|\|B\|
∥AB∥≤∥A∥∥B∥ .
常见的矩阵范数:
∥ A ∥ = max ∥ x ∥ 1 ∥ A x ∥ ∥ A ∥ 1 = max ∥ x ∥ 1 = 1 ∥ A x ∥ 1 = max k ∑ i = 1 n ∣ a i k ∣ ( 列和范数 ) ∥ A ∥ 2 = max ∥ x ∥ 2 = 1 ∥ A x ∥ 2 = λ 1 , λ 1 是 A T A 的最大特征值( A 的最大奇异值) . ∥ A ∥ ∞ = max ∣ x ∥ ∞ = 1 ∥ A x ∥ ∞ = max i ∑ k = 1 n ∣ a i k ∣ ( 行和范数 ) ∥ A ∥ F = ( ∑ i = 1 , k = 1 n ∣ a i k ∣ 2 ) 1 / 2 \begin{aligned} &\|A\|=\max _{\|x\|_{1}}\|A x\|\\ &\|A\|_{1}=\max _{\|x\|_{1}=1}\|A x\|_{1}=\max _{k} \sum_{i=1}^{n}\left|a_{i k}\right| (\text{列和范数})\\ &\|A\|_{2}=\max _{\|x\|_{2}=1}\|A x\|_{2}=\sqrt{\lambda_{1}}, \lambda_{1} \text { 是}A^{T} A\text{的最大特征值(}A\text{的最大奇异值)} . \\ &\|A\|_{\infty}=\max _{\mid x \|_{\infty}=1}\|A x\|_{\infty}=\max _{i} \sum_{k=1}^{n}\left|a_{i k}\right| (\text{行和范数}) \\ &\|A\|_{F}=\left(\sum_{i=1, k=1}^{n}\left|a_{i k}\right|^{2}\right)^{1 / 2} \quad \end{aligned} ∥A∥=∥x∥1max∥Ax∥∥A∥1=∥x∥1=1max∥Ax∥1=kmaxi=1∑n∣aik∣(列和范数)∥A∥2=∥x∥2=1max∥Ax∥2=λ1,λ1 是ATA的最大特征值(A的最大奇异值).∥A∥∞=∣x∥∞=1max∥Ax∥∞=imaxk=1∑n∣aik∣(行和范数)∥A∥F= i=1,k=1∑n∣aik∣2 1/2
而对于向量范数:
∥ x ∥ p = ( ∑ k = 1 n ∣ x k ∣ p ) 1 / p \|x\|_{p}=\left(\sum_{k=1}^{n}\left|x_{k}\right|^{p}\right)^{1 / p} ∥x∥p=(k=1∑n∣xk∣p)1/p
范数
∥
∗
∥
a
\|\ast\|_a
∥∗∥a和范数
∥
∗
∥
b
\|\ast\|_b
∥∗∥b等价:
c
1
∥
A
∥
a
≤
∥
A
∥
b
≤
c
2
∥
A
∥
a
c
1
′
∥
A
∥
b
≤
∥
A
∥
a
≤
c
2
∥
A
∥
b
\begin{aligned} c_{1}\|A\|_{a} \leq\|A\|_{b} \leq c_{2}\|A\|_{a} \\ c_{1}^{\prime}\|A\|_{b} \leq\|A\|_{a} \leq c_{2}\|A\|_{b} \end{aligned}
c1∥A∥a≤∥A∥b≤c2∥A∥ac1′∥A∥b≤∥A∥a≤c2∥A∥b
当
A
A
A的矩阵范数
∥
A
∥
<
1
\|{A}\|<1
∥A∥<1,则
I
±
A
I \pm A
I±A是非奇异可逆矩阵:
∥
(
I
±
A
)
−
1
∥
≤
1
1
−
∥
A
∥
\left\|(I \pm A)^{-1}\right\| \leq \frac{1}{1-\|A\|}
(I±A)−1
≤1−∥A∥1
前置知识2:舒尔补
A = [ B C D E ] , det ( B ) ≠ 0 A = [ I 0 D B − 1 I ] [ B 0 0 E − D B − 1 C ] [ I B − 1 C 0 I ] \begin{aligned} A & =\begin{bmatrix} B & C \\ D & E \end{bmatrix}, \operatorname{det}(B) \neq 0 \\ A & =\begin{bmatrix} I & 0 \\ D B^{-1} & I \end{bmatrix}\begin{bmatrix} B & 0 \\ 0 & E-D B^{-1} C \end{bmatrix}\begin{bmatrix} I & B^{-1} C \\ 0 & I \end{bmatrix} \end{aligned} AA=[BDCE],det(B)=0=[IDB−10I][B00E−DB−1C][I0B−1CI]
前置知识3:可约矩阵
定义:
如果通过行列变换可以变成这种形式:
P A Q = [ F 0 G H ] 或 [ F G 0 H ] \mathrm{PAQ}=\left[\begin{array}{c:c} \boldsymbol{F} & \boldsymbol{0} \\ \hdashline \boldsymbol{G} & \boldsymbol{H} \end{array}\right]或\left[\begin{array}{c:c} \boldsymbol{F} & \boldsymbol{G} \\ \hdashline \boldsymbol{0} & \boldsymbol{H} \end{array}\right] PAQ=[FG0H]或[F0GH]
左下角或右上角的 0 \boldsymbol{0} 0是零矩阵,则 A A A是可约矩阵。
可约矩阵:
[
2
0
1
0
8
6
7
5
4
2
3
1
4
0
3
0
]
⇒
[
1
2
3
4
5
6
7
8
0
0
1
2
0
0
3
4
]
\left[\begin{array}{llll}2 & 0 & 1 & 0 \\ 8 & 6 & 7 & 5 \\ 4 & 2 & 3 & 1 \\ 4 & 0 & 3 & 0\end{array}\right] \Rightarrow \left[\begin{array}{cc:cc} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ \hdashline 0 & 0 & 1 & 2 \\ 0 & 0 & 3 & 4 \end{array}\right]
2844062017330510
⇒
1500260037134824
不可约矩阵:
C
1
=
[
2
−
1
−
1
2
−
1
⋱
⋱
⋱
−
1
2
−
1
−
1
2
]
C_{1}=\left[\begin{array}{rrrrr} 2 & -1 & & & \\ -1 & 2 & -1 & & \\ & \ddots & \ddots & \ddots & \\ & & -1 & 2 & -1 \\ & & & -1 & 2 \end{array}\right]
C1=
2−1−12⋱−1⋱−1⋱2−1−12
注意上面这个矩阵对角占优,但不是严格对角占优。
前置知识4:谱半径
∣
A
−
λ
I
∣
=
0
|A-\lambda I|=0
∣A−λI∣=0
定义:设
λ
i
\lambda_i
λi是
A
A
A的特征值,
ρ
(
A
)
=
max
1
⩽
i
⩽
n
∣
λ
i
∣
\rho(A)=\max _{1 \leqslant i \leqslant n}\left|\lambda_{i}\right|
ρ(A)=1⩽i⩽nmax∣λi∣
称为矩阵A的谱半径。
定理:矩阵谱半径和矩阵范数有如下关系:
(1)若A是一般方阵,则P(A)不能作为矩阵的范数;
(2)若A是一般方阵,则谱半径不超过任意一种矩阵范数,即
ρ
(
A
)
≤
∥
A
∥
\rho(A)≤\|A\|
ρ(A)≤∥A∥
(3)若A为实对称矩阵,则谱半径可作矩阵的模,此时有
ρ
(
A
)
=
∥
A
∥
2
\rho(A)=\|A\|_{2}
ρ(A)=∥A∥2。
1.【线性方程组】直接求解:高斯消元法( L U LU LU分解)、 L D V LDV LDV分解、 L D L T LDL^T LDLT分解、 U D U T UDU^T UDUT分解
1.1 高斯消元法( L U LU LU分解)
针对线性方程组:
A
X
=
b
\mathrm{AX}=\mathrm{b}
AX=b
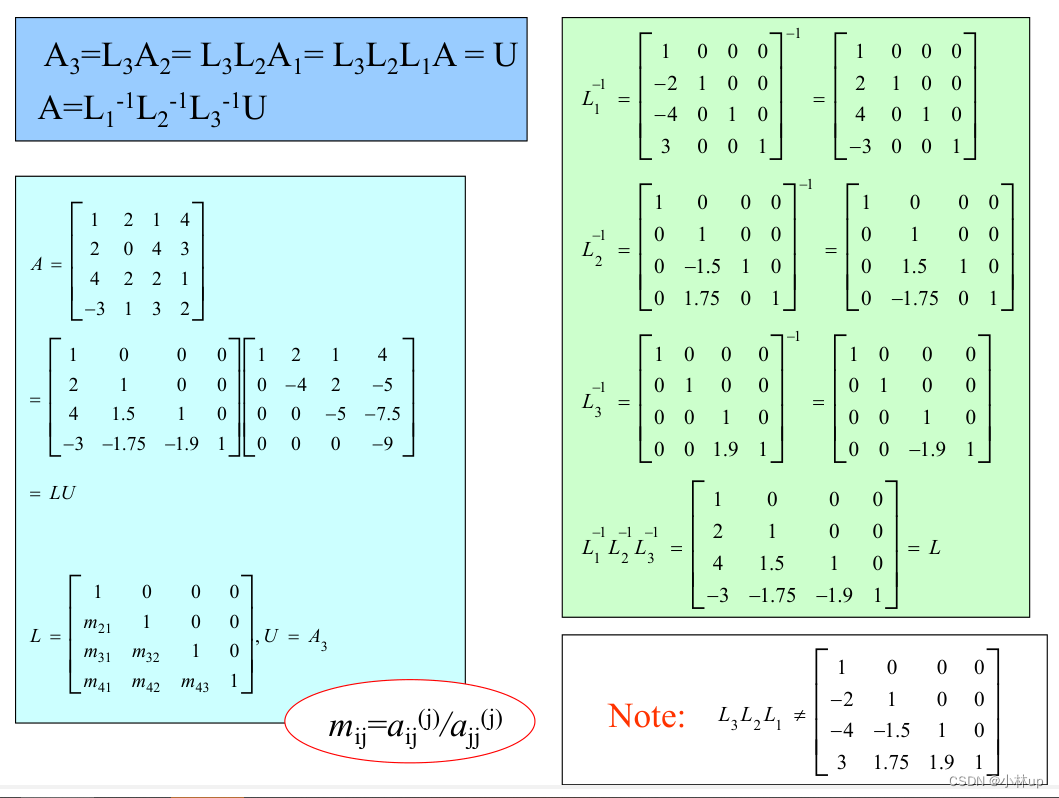
我们可以将 A \mathrm{A} A根据LU分解,分解为 A = L U \mathrm{A}=\mathrm{LU} A=LU,其中 L \mathrm{L} L和 U \mathrm{U} U分别是下三角和上三角矩阵。
L = [ ∗ 0 0 0 ∗ ∗ 0 0 ∗ ∗ ∗ 0 ∗ ∗ ∗ ∗ ] U = [ ∗ ∗ ∗ ∗ 0 ∗ ∗ ∗ 0 0 ∗ ∗ 0 0 0 ∗ ] L=\begin{bmatrix} \ast & 0 & 0 & 0 \\ \ast & \ast & 0 & 0 \\ \ast & \ast & \ast & 0 \\ \ast & \ast & \ast & \ast \end{bmatrix}\quad U=\begin{bmatrix} \ast & \ast & \ast & \ast \\ 0 & \ast & \ast & \ast \\ 0 & 0 & \ast & \ast \\ 0 & 0 & 0 & \ast \end{bmatrix} L= ∗∗∗∗0∗∗∗00∗∗000∗ U= ∗000∗∗00∗∗∗0∗∗∗∗
有:
A X = b ⇒ ( L U ) X = b ⇒ L ( U X ) = b ⇒ L X 1 = b U X = X 1 \begin{aligned}&\mathrm{AX}=\mathrm{b}\\ \Rightarrow&(\mathrm{LU}) \mathrm{X}=\mathrm{b} \\\Rightarrow&\mathrm{L}(\mathrm{UX})=\mathrm{b} \\ \Rightarrow &\mathrm{LX}_{1}=\mathrm{b}\quad \mathrm{UX}=\mathrm{X}_{1}\end{aligned} ⇒⇒⇒AX=b(LU)X=bL(UX)=bLX1=bUX=X1
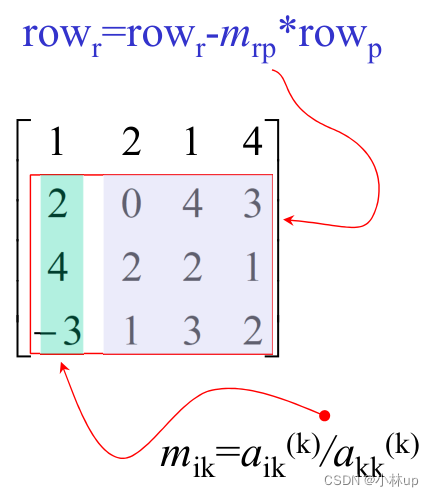
高斯消元变换三角阵:①交换行。②行乘一个因子。③某一行加到另一行上。例子:




高斯消元法中如果碰到对角线上的元素(主元素)消元为0,需要交换行,称作pivot element。
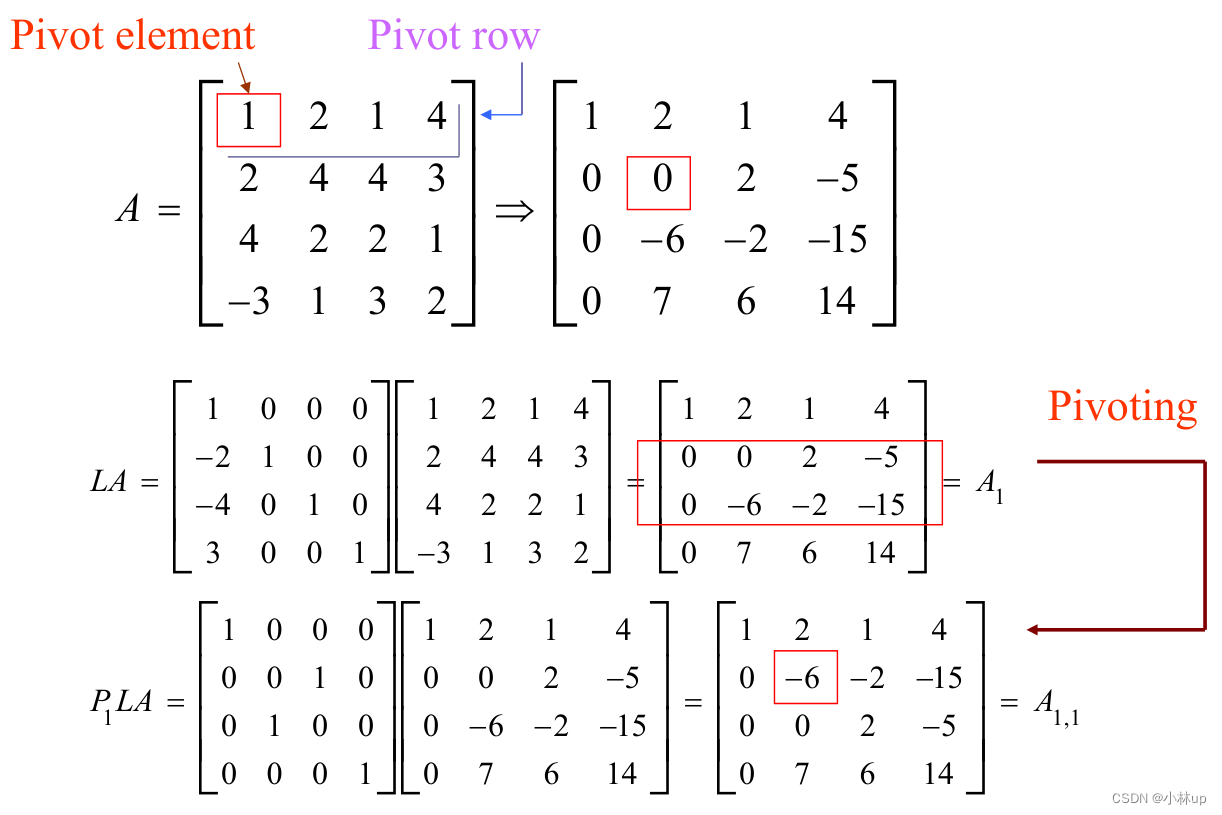
当主元素不合适由于舍入误差可能会无法求解!!

所以要选择合适的主元素:

当对角线的元素是0,可以换主元素。
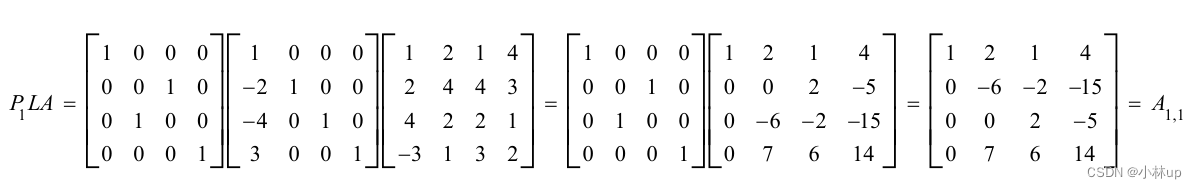
当然也可以提前换主元素。
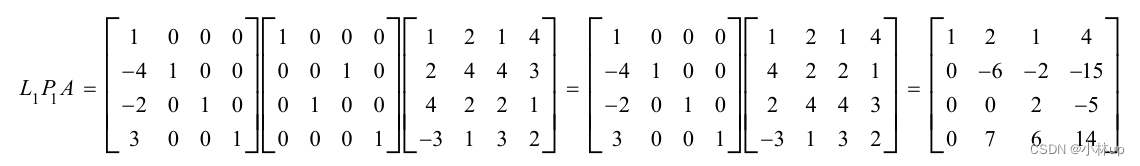
这可以表示为:
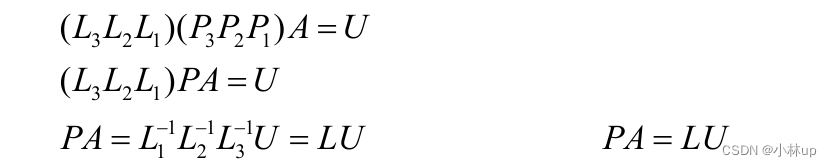
总结为:
A
x
=
b
P
A
=
L
U
⇒
P
A
x
=
P
b
=
b
ˉ
⇒
L
U
x
=
b
ˉ
⇒
L
x
ˉ
=
b
ˉ
U
x
=
x
ˉ
\begin{aligned} &A x=b \quad P A=L U \\ \Rightarrow&P A x=P b=\bar{b} \\ \Rightarrow&L U x=\bar{b} \\ \Rightarrow&L \bar{x}=\bar{b} \quad U x=\bar{x} \end{aligned}
⇒⇒⇒Ax=bPA=LUPAx=Pb=bˉLUx=bˉLxˉ=bˉUx=xˉ
计算的复杂度:
乘法和除法:
∑
p
=
1
N
−
1
(
N
−
p
)
(
N
−
p
+
1
)
=
N
3
−
N
3
\sum_{p=1}^{N-1}(N-p)(N-p+1)=\frac{N^{3}-N}{3}
∑p=1N−1(N−p)(N−p+1)=3N3−N
减法:
∑
p
=
1
N
−
1
(
N
−
p
)
(
N
−
p
)
=
2
N
3
−
3
N
2
+
N
6
\sum_{p=1}^{N-1}(N-p)(N-p)=\frac{2 N^{3}-3 N^{2}+N}{6}
∑p=1N−1(N−p)(N−p)=62N3−3N2+N
这里使用了公式:
∑
k
=
1
M
k
=
M
(
M
+
1
)
2
,
∑
k
=
1
M
k
2
=
M
(
M
+
1
)
(
2
M
+
1
)
6
\sum_{k=1}^{M} k=\frac{M(M+1)}{2}, \quad \sum_{k=1}^{M} k^{2}=\frac{M(M+1)(2 M+1)}{6}
k=1∑Mk=2M(M+1),k=1∑Mk2=6M(M+1)(2M+1)
1.2 L D V LDV LDV分解、 L D L T LDL^T LDLT分解、 U D U T UDU^T UDUT分解
定理:
a k k ( k ) ≠ 0 , k = 1 , 2 , … , n ⇔ ∣ A k ∣ ≠ 0 , k = 1 , 2 , … , n a_{k k}^{(k)} \neq 0, k=1,2, \ldots, n \Leftrightarrow\left|A_{k}\right| \neq 0, k=1,2, \ldots, n akk(k)=0,k=1,2,…,n⇔∣Ak∣=0,k=1,2,…,n其中 ∣ A k ∣ |A_{k}| ∣Ak∣是方阵的 k k k阶主子式。
进而我们可以知道 A = L U \mathrm{A}=\mathrm{LU} A=LU, L \mathrm L L是下三角矩阵, U \mathrm U U是上三角矩阵。 L \mathrm L L的对角线元素都是1, L \mathrm L L的行列式 ∣ L ∣ |\mathrm L| ∣L∣是1,所以 ∣ A ∣ = ∣ L U ∣ = ∣ U ∣ |\mathrm{A}|=\mathrm{|LU|}=|\mathrm{U}| ∣A∣=∣LU∣=∣U∣
让 U = D R \mathrm{U}=\mathrm{DR} U=DR,则有:
A = L D R \mathrm A=\mathrm{L D R} A=LDR
其中 L \mathrm L L是下三角矩阵, D \mathrm D D是对角矩阵, R \mathrm R R是上三角矩阵。
当 A \mathrm A A是对称阵, A = L D L T \mathrm{A}=\mathrm{LDL}^{\mathrm{T}} A=LDLT
类似的对称阵也可以表示为 A = U D U T \mathrm{A}=\mathrm{UDU}^{\mathrm{T}} A=UDUT
还有就是求逆矩阵的方法:
[ A I ] ⟶ Row Transformation [ I A − 1 ] \left[\begin{array}{ll} A & I \end{array}\right] \stackrel{\text { Row Transformation }}{\longrightarrow}\left[\begin{array}{ll} I & A^{-1} \end{array}\right] [AI]⟶ Row Transformation [IA−1]
总结:直接求解线性方程组:
1.核心算法是LU分解。 P B = L U B − 1 = U − 1 L − 1 P \begin{aligned} P B & = L U \\ B^{-1} & = U^{-1} L^{-1} P \end{aligned} PBB−1=LU=U−1L−1P
2.迭代求解器可能不能收敛或计算成本较高。
1.3 误差分析(从条件数的角度)
矩阵范数回顾前置知识1.
①给
b
b
b一个小的扰动对
x
x
x有什么影响嘛?
A x = b A ( x + δ x ) = b + δ b A δ x = δ b ∥ δ x ∥ = ∥ A − 1 δ b ∥ ≤ ∥ A − 1 ∥ δ b ∥ ∥ A x ∥ ≤ ∥ A ∥ ∥ x ∥ , ∥ x ∥ ≥ ∥ A x ∥ ∥ A ∥ = ∥ b ∥ ∥ A ∥ ∥ δ x ∥ ∥ x ∥ ≤ ∥ A ∥ ∥ A − 1 ∥ ∥ δ b ∥ ∥ b ∥ = cond ( A ) ∥ δ b ∥ ∥ b ∥ \begin{aligned} &A x=b \\ &A(x+\delta x)=b+\delta b \\ &A \delta x=\delta b \\ &\|\delta x\|=\left\|A^{-1} \delta b\right\| \leq\left\|A^{-1}\right\| \delta b \| \\ &\|A x\| \leq\|A\|\|x\|, \quad\|x\| \geq \frac{\|A x\|}{\|A\|}=\frac{\|b\|}{\|A\|} \\ &\frac{\|\delta x\|}{\|x\|} \leq\|A\|\left\|A^{-1}\right\| \frac{\|\delta b\|}{\|b\|}=\operatorname{cond}(A) \frac{\|\delta b\|}{\|b\|} \end{aligned} Ax=bA(x+δx)=b+δbAδx=δb∥δx∥= A−1δb ≤ A−1 δb∥∥Ax∥≤∥A∥∥x∥,∥x∥≥∥A∥∥Ax∥=∥A∥∥b∥∥x∥∥δx∥≤∥A∥ A−1 ∥b∥∥δb∥=cond(A)∥b∥∥δb∥
②给 A A A一个小的扰动对 x x x有什么影响嘛?
A x = b ( A + δ A ) ( x + δ x ) = b A δ x + δ A ( x + δ x ) = 0 ∥ δ x ∥ = ∥ A − 1 δ A ( x + δ x ) ∥ ≤ ∥ A − 1 ∥ δ A ∥ ∥ ( ∥ x ∥ + ∥ δ x ∥ ) ∥ δ x ∥ ∥ x ∥ ≤ ∥ A − 1 ∥ ∥ δ A ∥ ( 1 + ∥ δ x ∥ ∥ x ∥ ) ∥ δ x ∥ ∥ x ∥ ≤ ∥ A − 1 ∥ ∥ δ A ∥ 1 − ∥ A − 1 ∥ ∥ δ A ∥ = ∥ A − 1 ∥ ∥ A ∥ ∥ δ A ∥ ∥ A ∥ 1 − ∥ A − 1 ∥ ∥ A ∥ ∥ δ A ∥ ∥ A ∥ = c o n d ( A ) ∣ ∥ δ A ∥ ∥ A ∥ 1 − c o n d ( A ) ∣ ∥ δ A ∥ ∥ A ∥ \begin{aligned} &A x = b \\ &(A+\delta A)(x+\delta x) = b \\ &A \delta x+\delta A(x+\delta x) = 0 \\ &\|\delta x\| = \left\|A^{-1} \delta A(x+\delta x)\right\| \leq\left\|A^{-1}\right\| \delta A\|\|(\|x\|+\|\delta x\|) \\ &\frac{\|\delta x\|}{\|x\|} \leq\left\|A^{-1}\right\|\|\delta A\|\left(1+\frac{\|\delta x\|}{\|x\|}\right) \\ &\frac{\|\delta x\|}{\|x\|} \leq \frac{\left\|A^{-1}\right\|\|\delta A\|}{1-\left\|A^{-1}\right\|\|\delta A\|}=\frac{\|A^{-1}\|\|A\|\frac{\|\delta A\|} {\|A\|}}{1-\|A^{-1}\|\|A\|\frac{\|\delta A\|} {\|A\|}}=\frac{cond(A)|\frac{\|\delta A\|} {\|A\|}}{1-cond(A)|\frac{\|\delta A\|} {\|A\|}} \end{aligned} Ax=b(A+δA)(x+δx)=bAδx+δA(x+δx)=0∥δx∥= A−1δA(x+δx) ≤ A−1 δA∥∥(∥x∥+∥δx∥)∥x∥∥δx∥≤ A−1 ∥δA∥(1+∥x∥∥δx∥)∥x∥∥δx∥≤1−∥A−1∥∥δA∥ A−1 ∥δA∥=1−∥A−1∥∥A∥∥A∥∥δA∥∥A−1∥∥A∥∥A∥∥δA∥=1−cond(A)∣∥A∥∥δA∥cond(A)∣∥A∥∥δA∥
这里需要假设 1 − c o n d ( A ) ∥ δ A ∥ ∥ A ∥ ≥ 0 1-cond(A)\frac{\|\delta A\|} {\|A\|}\ge0 1−cond(A)∥A∥∥δA∥≥0或 δ A \delta{A} δA足够小。其中 c o n d ( A ) = ∥ A − 1 ∥ ∥ A ∥ cond(A)=\left\|A^{-1}\right\|\|A\| cond(A)= A−1 ∥A∥称为条件数。
当条件数很大时矩阵是病态的。例如:
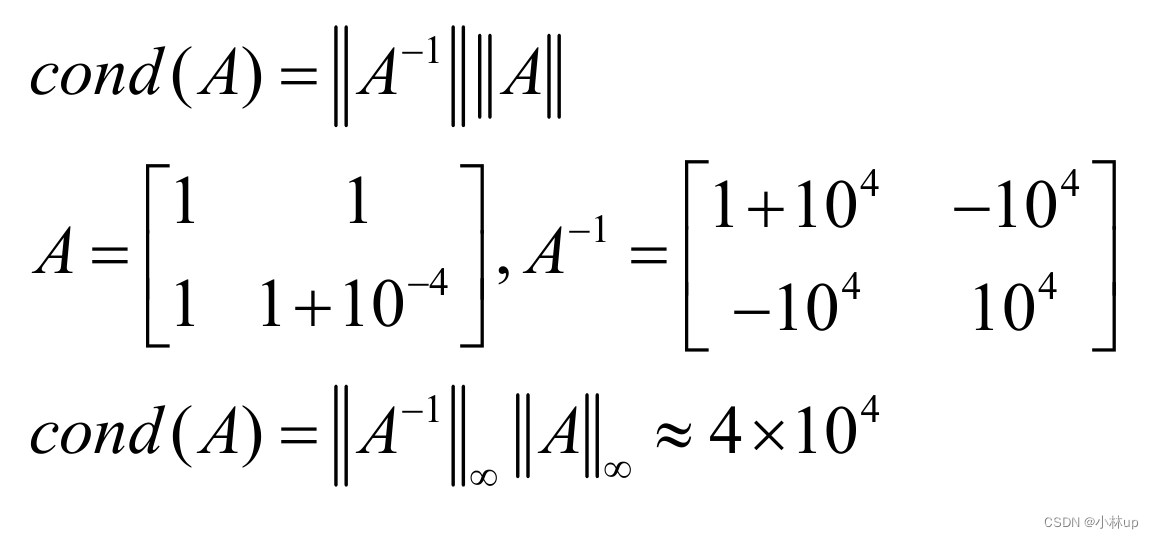

其他判断条件数的方法
- 当两行中的对应元素的比率非常接近时,cond(A)可能很大。
- 元素之间的差异很大,cond(A)也可能很大。
- 对A或b做一个小的扰动,然后解方程。如果解差很大,矩阵就没有条件。
于是我们就想把病态的矩阵转为非病态的矩阵:左乘一个矩阵,改变稳定性。
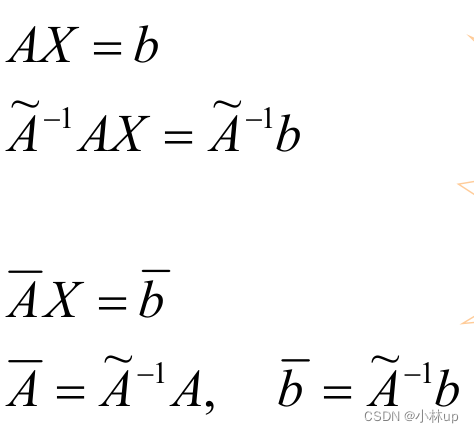
找到合适的
A
~
−
1
\widetilde{A}^{-1}
A
−1是关键
2. 【线性方程组】间接迭代求解:Jacobi方法, Gauss-Seidel方法
我们能不能使用类似不动点迭代的思想进行求解呢?我们要考虑:
- 怎么选择迭代形式
- 迭代要收敛
- 收敛的速度也要保证
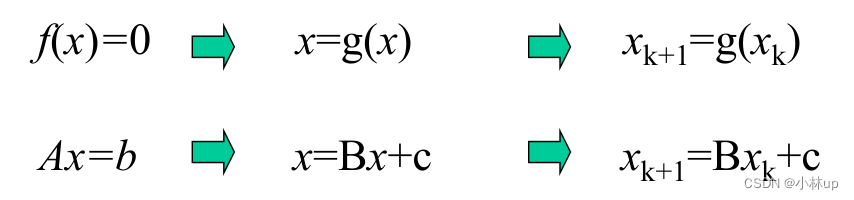
2.1 Jacobi方法
A = L + D + U x = D − 1 ( b − L x − U x ) x ( k + 1 ) = D − 1 ( b − L x ( k ) − U x ( k ) ) \begin{aligned} {A} & = {L}+{D}+{U} \\ {x} & = {D}^{-1}({~b}-{Lx}-{Ux}) \\ {x}^{({k}+1)} & = {D}^{-1}\left({~b}-{Lx}{ }^{({k})}-{Ux}^{({k})}\right) \end{aligned} Axx(k+1)=L+D+U=D−1( b−Lx−Ux)=D−1( b−Lx(k)−Ux(k))
x ( k + 1 ) = B x ( k ) + c , B = − D − 1 ( L + U ) , c = D − 1 b x^{({k}+1)}={B} x^{({k})}+{c}, \quad {B}=-{D}^{-1}({~L}+{U}), \quad {c}={D}^{-1} {b} x(k+1)=Bx(k)+c,B=−D−1( L+U),c=D−1b
例子
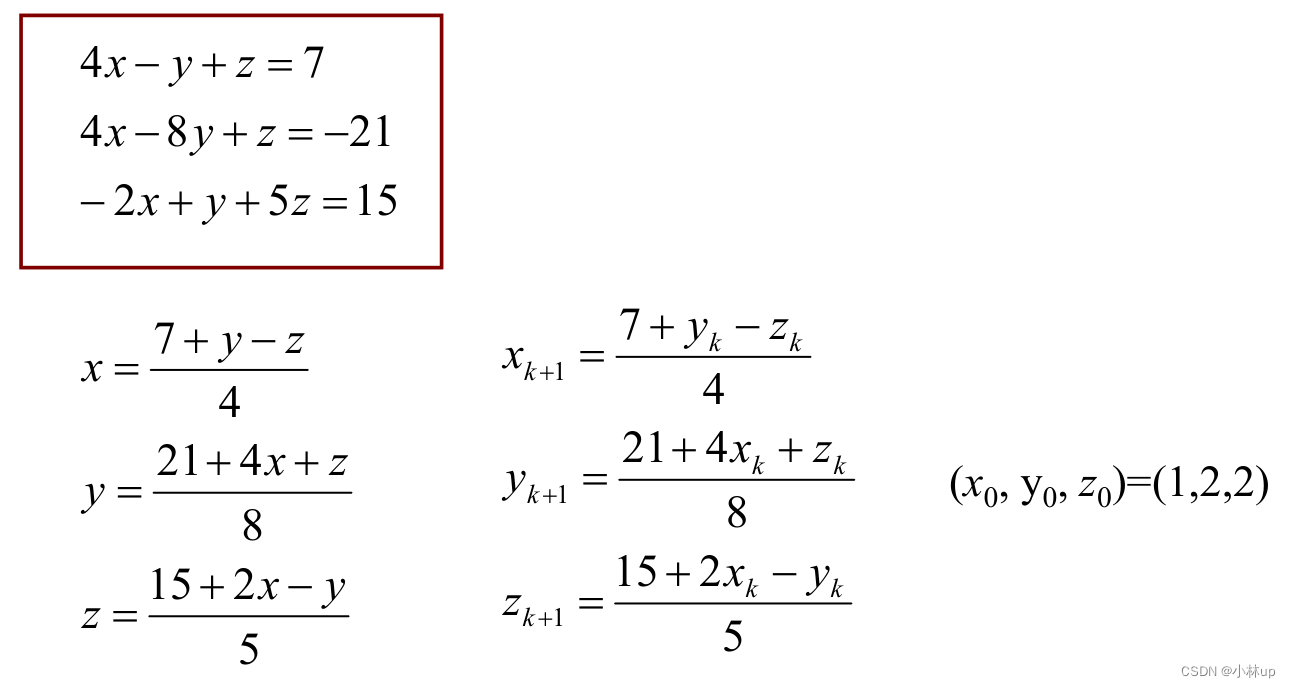
具体编程的实现可以有:
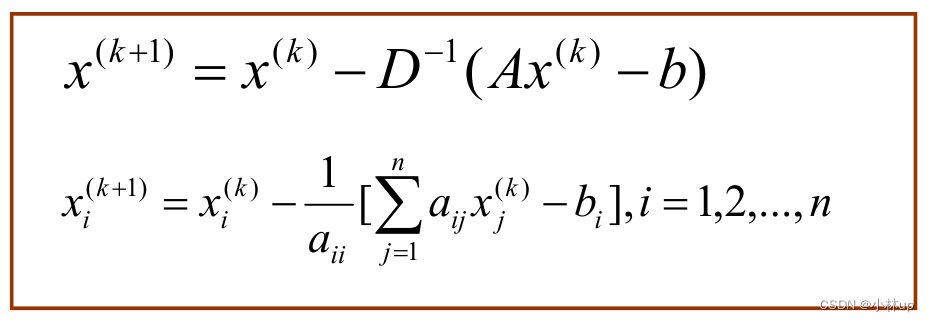
或者
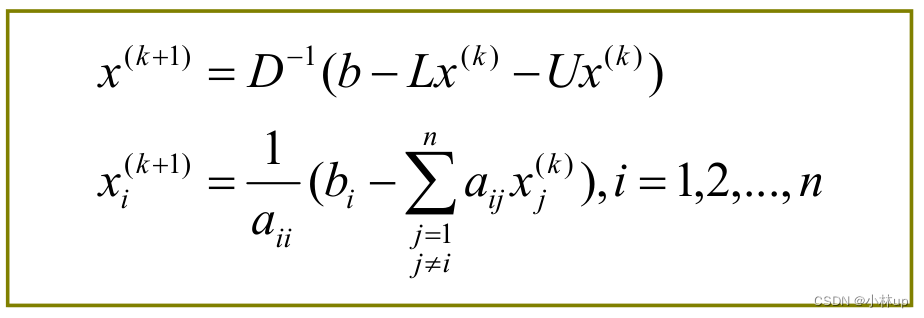
然而同一个方程组不同的方程顺序可能会不收敛。

所以什么时候会收敛呢?
定义:
矩阵 A A A严格对角占优: ∣ a k k ∣ > ∑ j = 1 , j ≠ k N ∣ a k j ∣ k = 1 , 2 , … , N \left|a_{k k}\right|>\sum_{j=1, j \neq k}^{N}\left|a_{k j}\right| \quad k=1,2, \ldots, N ∣akk∣>j=1,j=k∑N∣akj∣k=1,2,…,N
矩阵 A A A表示为:
A = [ a 11 a 12 ⋯ a 1 N a 21 a 22 ⋯ a 2 N ⋮ ⋮ ⋮ a N 1 a N 2 ⋯ a N N ] A=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1 N} \\ a_{21} & a_{22} & \cdots & a_{2 N} \\ \vdots & \vdots & & \vdots \\ & & & \\ a_{N 1} & a_{N 2} & \cdots & a_{N N} \end{bmatrix} A= a11a21⋮aN1a12a22⋮aN2⋯⋯⋯a1Na2N⋮aNN
例子:
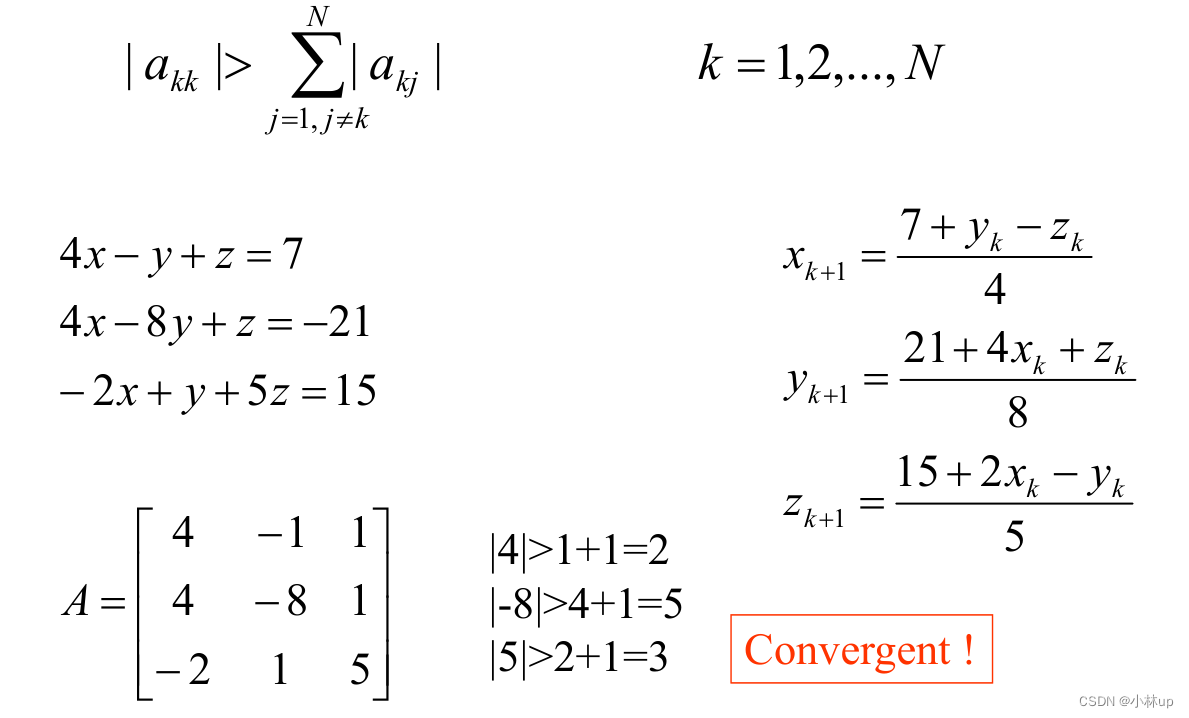

严格对角占优只能算是Jacobi方法的一个充分条件。
2.2 Gauss-Seidel方法
A = L + D + U x = D − 1 ( b − L x − U x ) x ( k + 1 ) = D − 1 ( b − L x ( k + 1 ) − U x ( k ) ) \begin{aligned} &{A} = {L}+{D}+{U} \\ &{x} = {D}^{-{1}}({b}-{L} {x}-{U} {x})\\ &{x}^{({k}+1)}={D}^{-1}\left({b}-{L} {x}^{({k}+1)}-{U} {x}^{({k})}\right) \end{aligned} A=L+D+Ux=D−1(b−Lx−Ux)x(k+1)=D−1(b−Lx(k+1)−Ux(k))
A = L + D + U ( L + D ) x ( k + 1 ) + U x ( k ) = b x ( k + 1 ) = − ( L + D ) − 1 U x ( k ) + ( L + D ) − 1 b \begin{aligned} &{A} = {L}+{D}+{U} \\ &({L}+{D}) {x}^{({k}+1)}+{U} {x}^{({k})} = {b} \\ &{x}^{({k}+1)}=-({L}+{D})^{-1} {U} {x}^{({k})}+({L}+{D})^{-1} {b}\\ \end{aligned} A=L+D+U(L+D)x(k+1)+Ux(k)=bx(k+1)=−(L+D)−1Ux(k)+(L+D)−1b
x
(
k
+
1
)
=
B
x
(
k
)
+
c
,
B
=
−
(
L
+
D
)
−
1
U
,
c
=
(
L
+
D
)
−
1
b
x^{({k}+1)}={B} x^{({k})}+{c}, \quad {B}=-({L}+{D})^{-1} {U} , \quad {c}=({L}+{D})^{-1} {b}
x(k+1)=Bx(k)+c,B=−(L+D)−1U,c=(L+D)−1b

迭代速度比Jacobi方法更快!
2.3 Jacobi方法, Gauss-Seidel方法收敛的条件
充分条件1
矩阵 A A A满足下面任一①严格对角占优 ②**不可约矩阵(回顾前置知识3),使用Jacobi方法, Gauss-Seidel方法都收敛。
充分必要条件
矩阵的谱半径小于1。
ρ
(
B
)
=
max
i
∣
λ
i
∣
<
1
∣
B
−
λ
i
I
∣
=
0
\rho(B)=\max _{i}\left|\lambda_{i}\right|<1\quad \left|B-\lambda_{i} I\right|=0
ρ(B)=imax∣λi∣<1∣B−λiI∣=0
以下是对实对称阵说明
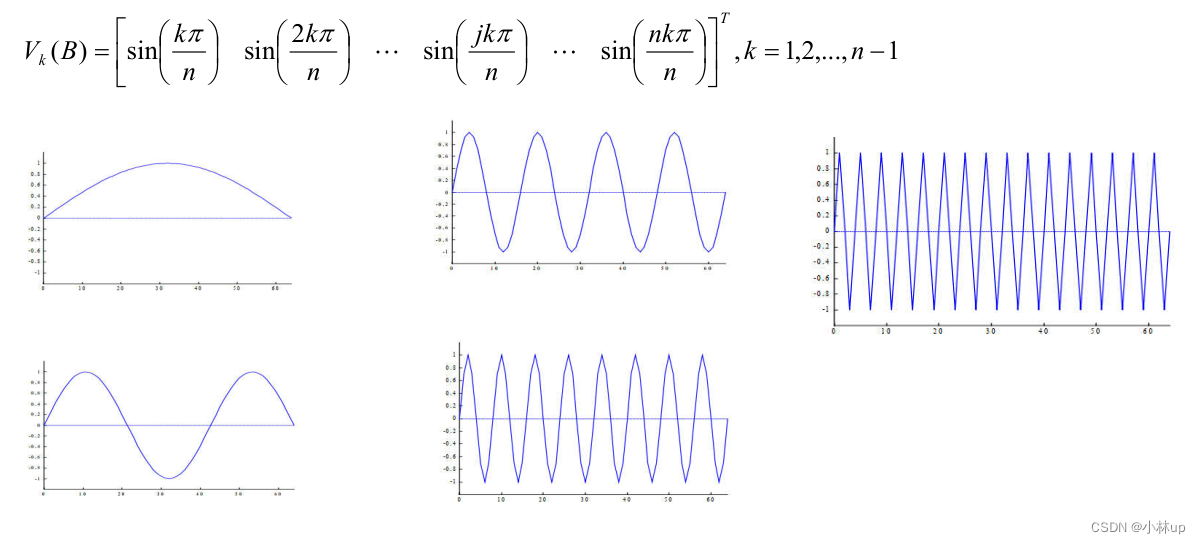
x = B x + g x ( k + 1 ) = B x ( k ) + g e ( k + 1 ) = B e ( k ) = B k + 1 e ( 0 ) 【 e ( k + 1 ) = x ( k + 1 ) − x ( k ) 】 e ( 0 ) = c 1 V 1 + c 2 V 2 + … + c n V n , B V i = λ i V i e ( k + 1 ) = c 1 λ 1 k + 1 V 1 + c 2 λ 2 k + 1 V 2 + … + c n λ n k + 1 V n → 0 when ∣ λ i ∣ < 1 \begin{aligned} &x = B x+g \\ &x^{(k+1)} = B x^{(k)}+g \\ &e^{(k+1)} = B e^{(k)} = B^{k+1} e^{(0)} 【e^{(k+1)} =x^{(k+1)} -x^{(k)}】\\ & e^{(0)} = c_{1} V_{1}+c_{2} V_{2}+\ldots+c_{n} V_{n}, \quad B V_{i} = \lambda_{i} V_{i} \\ &e^{(k+1)} = c_{1} \lambda_{1}^{k+1} V_{1}+c_{2} \lambda_{2}^{k+1} V_{2}+\ldots+c_{n} \lambda_{n}^{k+1} V_{n} \rightarrow 0 \quad \text { when }\left|\lambda_{i}\right|<1 \end{aligned} x=Bx+gx(k+1)=Bx(k)+ge(k+1)=Be(k)=Bk+1e(0)【e(k+1)=x(k+1)−x(k)】e(0)=c1V1+c2V2+…+cnVn,BVi=λiVie(k+1)=c1λ1k+1V1+c2λ2k+1V2+…+cnλnk+1Vn→0 when ∣λi∣<1
对一般的矩阵形式可以用Jordan形式证明
B = T J T − 1 B k = T J k T − 1 J k = diag ( J r 1 k ( λ 1 ) , J r 2 k ( λ 2 ) , … , J r p k ( λ p ) ) → 0 , when ∣ λ i ∣ < 1 J r i ( λ i ) = [ λ i 1 λ i 1 ⋱ 1 λ i ] \begin{aligned} &B = T J T^{-1} \\ &B^{k} = T J^{k} T^{-1} \\ &J^{k} = \operatorname{diag}\left(J_{r_{1}}^{k}\left(\lambda_{1}\right), J_{r_{2}}^{k}\left(\lambda_{2}\right), \ldots, J_{r_{p}}^{k}\left(\lambda_{p}\right)\right) \rightarrow 0, \text { when }\left|\lambda_{i}\right|<1 \\ &J_{r_{i}}\left(\lambda_{i}\right) = \begin{bmatrix} \lambda_{i} & 1 & & \\ & \lambda_{i} & 1 & \\ & & \ddots & 1 \\ & & \lambda_{i} \end{bmatrix} \end{aligned} B=TJT−1Bk=TJkT−1Jk=diag(Jr1k(λ1),Jr2k(λ2),…,Jrpk(λp))→0, when ∣λi∣<1Jri(λi)= λi1λi1⋱λi1
定理:对于矩阵的任意范数,谱半径都小于矩阵的范数。
ρ
(
B
)
≤
∥
B
∥
\rho(B) \leq\|B\|
ρ(B)≤∥B∥
于是有
充分条件2
满足条件 ∥ B ∥ < 1 \|B\|<1 ∥B∥<1,矩阵 A A A使用Jacobi方法, Gauss-Seidel方法都收敛。
说明:以下等价
B
k
→
0
⇔
∥
B
k
∥
→
0
⇔
ρ
(
B
)
<
1
B^{k} \rightarrow 0 \Leftrightarrow\left\|B^{k}\right\| \rightarrow 0 \Leftrightarrow \rho(B)<1\\
Bk→0⇔
Bk
→0⇔ρ(B)<1
∥ B k ∥ ≤ ∥ B ∥ ∥ B k − 1 ∥ ≤ ∥ B ∥ k \left\|B^{k}\right\| \leq\|B\|\left\|B^{k-1}\right\| \leq\|B\|^{k} Bk ≤∥B∥ Bk−1 ≤∥B∥k
充分条件3
定理:矩阵
A
A
A满足下面任一条件:①严格对角占优 ②**不可约矩阵(回顾前置知识3),并且对角线上元素大于0,
A
A
A是个正定矩阵!
如果矩阵 A A A是对称正定矩阵,使用Jacobi方法, Gauss-Seidel方法都收敛。
一张关系图说明收敛的条件
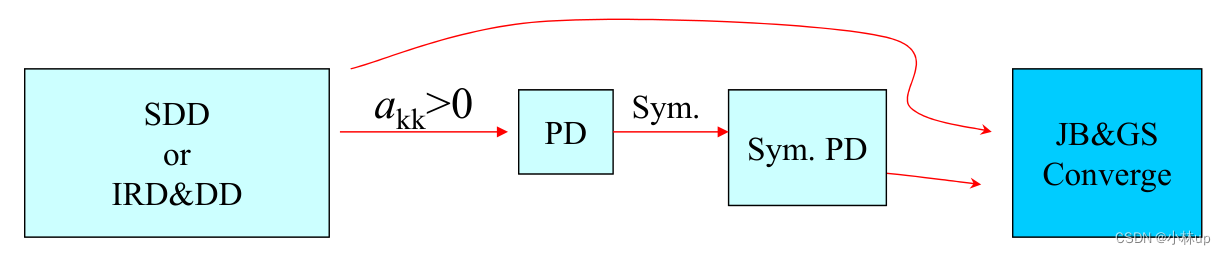
2.4 预测迭代次数
定理:设基本迭代的迭代矩阵 ∥ B ∥ = q < 1 \|B\|=q<1 ∥B∥=q<1,若 ∥ x ( k + 1 ) − x ( k ) ∥ ⩽ ε \left\|x^{(k+1)}-x^{(k)}\right\| \leqslant \varepsilon x(k+1)−x(k) ⩽ε,则 ∥ x ( k ) − x ∥ ⩽ ε 1 − q \left\|x^{(k)}-x\right\| \leqslant \frac{\varepsilon}{1-q} x(k)−x ⩽1−qε
容易证明: ∥ X k − X ∗ ∥ ≤ 1 1 − ∥ B ∥ ∥ X k + 1 − X k ∥ ∥ X k − X ∗ ∥ ≤ ∥ B ∥ k 1 − ∥ B ∥ ∥ X 1 − X 0 ∥ \begin{aligned} \left\|X_{k}-X^{*}\right\| \leq\frac{1}{1-\|B\|}\left\|X_{k+1}-X_{k}\right\| \\ \left\|X_{k}-X^{*}\right\| \leq \frac{\|B\|^{k}}{1-\|B\|}\left\|X_{1}-X_{0}\right\| \end{aligned} ∥Xk−X∗∥≤1−∥B∥1∥Xk+1−Xk∥∥Xk−X∗∥≤1−∥B∥∥B∥k∥X1−X0∥
这个定理使用的两种方式:
1.预测需要的迭代次数
2.使用
∣
x
k
+
1
−
x
k
∣
|x_{k+1}-x_k|
∣xk+1−xk∣看是否停止迭代。
预测迭代次数类似不动点迭代收敛的推导: 就不具体展开了。
2.5 连续超松弛方法(The Method of Successive Over-Relaxation【SOR】)
( L + D ) x ~ ( k + 1 ) + U x ( k ) = b x ( k + 1 ) = ω x ~ ( k + 1 ) + ( 1 − ω ) x ( k ) x i ( k + 1 ) = ( 1 − ω ) x i ( k ) + ω a i i ( b i − ∑ j = 1 i − 1 a i j x j ( k + 1 ) − ∑ j = i + 1 n a i j x j ( k ) ) = ( 1 − ω ) x i ( k ) + ω a i i ( b i − ∑ j = 1 i − 1 a i j x j ( k + 1 ) − a i i x i ( k ) − ∑ j = i + 1 n a i j x j ( k ) + a i i x i ( k ) ) = x i ( k ) + ω a i i ( b i − ∑ j = 1 i − 1 a i j x j ( k + 1 ) − ∑ j = i n a i j x j ( k ) ) ⇒ x ( k + 1 ) = x ( k ) + ω D − 1 ( b − L x ( k + 1 ) − D x ( k ) − U x ( k ) ) ⇒ D x ( k + 1 ) = D x ( k ) + ω ( b − L x ( k + 1 ) − D x ( k ) − U x ( k ) ) ⇒ ( D + ω L ) x ( k + 1 ) = [ ( 1 − ω ) D − ω U ] x ( k ) + ω b ⇒ x ( k + 1 ) = ( D + ω L ) − 1 [ ( 1 − ω ) D − ω U ] x ( k ) + ω ( D + ω L ) − 1 b \begin{aligned} &(L+D) \tilde{x}^{(k+1)}+U x^{(k)} = b \\ &x^{(k+1)} = \omega \tilde{x}^{(k+1)}+(1-\omega) x^{(k)} \\ &x_{i}^{(k+1)} = (1-\omega) x_{i}^{(k)}+\frac{\omega}{a_{i i}}\left(b_{i}-\sum_{j = 1}^{i-1} a_{i j} x_{j}^{(k+1)}-\sum_{j = i+1}^{n} a_{i j} x_{j}^{(k)} \right)\\ &= (1-\omega) x_{i}^{(k)}+\frac{\omega}{a_{i i}}\left(b_{i}-\sum_{j = 1}^{i-1} a_{i j} x_{j}^{(k+1)}-a_{i i} x_{i}^{(k)}-\sum_{j = i+1}^{n} a_{i j} x_{j}^{(k)}+a_{i i} x_{i}^{(k)}\right) \\ & = x_{i}^{(k)}+\frac{\omega}{a_{i i}}\left(b_{i}-\sum_{j = 1}^{i-1} a_{i j} x_{j}^{(k+1)}-\sum_{j = i}^{n} a_{i j} x_{j}^{(k)}\right)\\ \Rightarrow &x^{(k+1)} = x^{(k)}+\omega D^{-1}\left(b-L x^{(k+1)}-D x^{(k)}-U x^{(k)}\right) \\ \Rightarrow&D x^{(k+1)} = D x^{(k)}+\omega\left(b-L x^{(k+1)}-D x^{(k)}-U x^{(k)}\right) \\ \Rightarrow&(D+\omega L) x^{(k+1)} = [(1-\omega) D-\omega U] x^{(k)}+\omega b \\ \Rightarrow&x^{(k+1)} = (D+\omega L)^{-1}[(1-\omega) D-\omega U] x^{(k)}+\omega(D+\omega L)^{-1} b \end{aligned} ⇒⇒⇒⇒(L+D)x~(k+1)+Ux(k)=bx(k+1)=ωx~(k+1)+(1−ω)x(k)xi(k+1)=(1−ω)xi(k)+aiiω(bi−j=1∑i−1aijxj(k+1)−j=i+1∑naijxj(k))=(1−ω)xi(k)+aiiω(bi−j=1∑i−1aijxj(k+1)−aiixi(k)−j=i+1∑naijxj(k)+aiixi(k))=xi(k)+aiiω(bi−j=1∑i−1aijxj(k+1)−j=i∑naijxj(k))x(k+1)=x(k)+ωD−1(b−Lx(k+1)−Dx(k)−Ux(k))Dx(k+1)=Dx(k)+ω(b−Lx(k+1)−Dx(k)−Ux(k))(D+ωL)x(k+1)=[(1−ω)D−ωU]x(k)+ωbx(k+1)=(D+ωL)−1[(1−ω)D−ωU]x(k)+ω(D+ωL)−1b
x ( k + 1 ) = B x ( k ) + c , B = ( D + ω L ) − 1 [ ( 1 − ω ) D − ω U ] , c = ω ( D + ω L ) − 1 b x^{({k}+1)}={B} x^{({k})}+{c}, \quad {B}= (D+\omega L)^{-1}[(1-\omega) D-\omega U] , \quad {c}=\omega(D+\omega L)^{-1} b x(k+1)=Bx(k)+c,B=(D+ωL)−1[(1−ω)D−ωU],c=ω(D+ωL)−1b
还有另一种形式:
(
L
+
D
)
x
~
(
k
+
1
)
+
U
x
(
k
)
=
b
x
(
k
+
1
)
=
ω
x
~
(
k
+
1
)
+
(
1
−
ω
)
x
(
k
)
⇒
x
(
k
+
1
)
=
ω
(
−
(
L
+
D
)
−
1
U
x
(
k
)
+
(
L
+
D
)
−
1
b
)
+
(
1
−
ω
)
x
(
k
)
⇒
x
(
k
+
1
)
=
[
(
1
−
ω
)
I
−
ω
(
L
+
D
)
−
1
U
]
x
(
k
)
+
ω
(
L
+
D
)
−
1
b
\begin{aligned} &(L+D) \tilde{x}^{(k+1)}+U x^{(k)} = b \\ &x^{(k+1)} = \omega \tilde{x}^{(k+1)}+(1-\omega) x^{(k)} \\ \Rightarrow&x^{(k+1)} = \omega \left( -({L}+{D})^{-1} {U} {x}^{({k})}+({L}+{D})^{-1} {b}\right)+(1-\omega) x^{(k)}\\ \Rightarrow&x^{(k+1)}=\left[(1-\omega) I-\omega(L+D)^{-1} U\right] x^{(k)}+\omega(L+D)^{-1} b \end{aligned}
⇒⇒(L+D)x~(k+1)+Ux(k)=bx(k+1)=ωx~(k+1)+(1−ω)x(k)x(k+1)=ω(−(L+D)−1Ux(k)+(L+D)−1b)+(1−ω)x(k)x(k+1)=[(1−ω)I−ω(L+D)−1U]x(k)+ω(L+D)−1b
x ( k + 1 ) = B x ( k ) + c , B = [ ( 1 − ω ) I − ω ( L + D ) − 1 U ] , c = ω ( L + D ) − 1 b x^{({k}+1)}={B} x^{({k})}+{c}, \quad {B}=\left[(1-\omega) I-\omega(L+D)^{-1} U\right] , \quad {c}=\omega(L+D)^{-1} b x(k+1)=Bx(k)+c,B=[(1−ω)I−ω(L+D)−1U],c=ω(L+D)−1b
可以根据 ω 可以根据\omega 可以根据ω取值不同分类如下:
0 < ω < 2 ω = 1 : Gauss - Seidel 0 < ω < 1 : Under - Relaxation 1 < ω < 2 : SOR \begin{align} &0<\omega<2 \\ &\omega = 1: \text { Gauss - Seidel } \\ &0<\omega<1: \text { Under - Relaxation } \\ &1<\omega<2: \text { SOR } \end{align} 0<ω<2ω=1: Gauss - Seidel 0<ω<1: Under - Relaxation 1<ω<2: SOR
SOR 收敛的条件和Jacobi方法, Gauss-Seidel方法相同:
1.当系数矩阵A为强对角占优矩阵时,SOR方法收敛;
2.当系数矩阵A为不可约对角占优矩阵时,SOR方法收敛;
3.当系数矩阵A为对称正定矩阵时,SOR方法收敛。
x ( k + 1 ) = B x ( k ) + c x^{({k}+1)}={B} x^{({k})}+{c} x(k+1)=Bx(k)+c
B
B
B是关于松弛因子
ω
\omega
ω的一个函数,所以
ω
\omega
ω应该取多少呢?
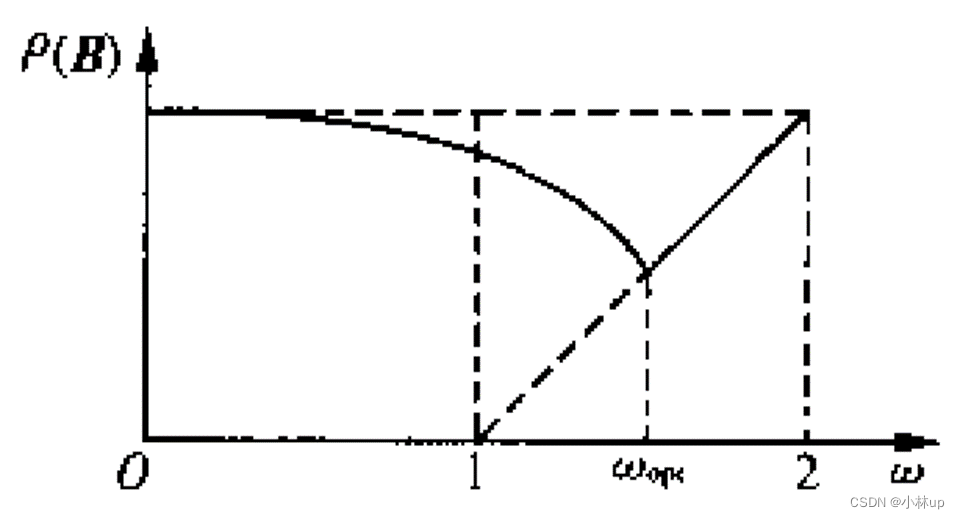
可惜的是, ω o p t \omega_{opt} ωopt无法准确求得,只能估算,下面给出两种估算方法。
方法1: 先用 ω = 1 \omega=1 ω=1算得 x ( 1 ) x^{(1)} x(1)和 x ( 2 ) x^{(2)} x(2),再用 ω = 1.1 \omega=1.1 ω=1.1算得 x ~ ( 1 ) \tilde x^{(1)} x~(1)和 x ~ ( 2 ) \tilde x^{(2)} x~(2);比较 ∥ x ( 1 ) − x ( 2 ) ∥ \|x^{(1)}-x^{(2)}\| ∥x(1)−x(2)∥和 ∥ x ~ ( 1 ) − x ~ ( 2 ) ∥ \|\tilde x^{(1)}-\tilde x^{(2)}\| ∥x~(1)−x~(2)∥的大小,量值 ∥ x ~ ( 1 ) − x ~ ( 2 ) ∥ \|\tilde x^{(1)}-\tilde x^{(2)}\| ∥x~(1)−x~(2)∥较大说明取 ω = 1.1 \omega=1.1 ω=1.1时迭代收敛快:继续选 ω = 1.2 \omega=1.2 ω=1.2计算且与 ω = 1.1 \omega=1.1 ω=1.1的情形比较,不断改进 ω \omega ω的值直到接近 ω \omega ω为止、
方法2: 用 ω = 1.9 \omega=1.9 ω=1.9和 ω = 1.8 \omega=1.8 ω=1.8计算,判断比较相应松弛迭代收敛的快慢表现;不断改进参数w的取值,在 ω o p t \omega_{opt } ωopt附近还可作些适当的微调处理。
例子:
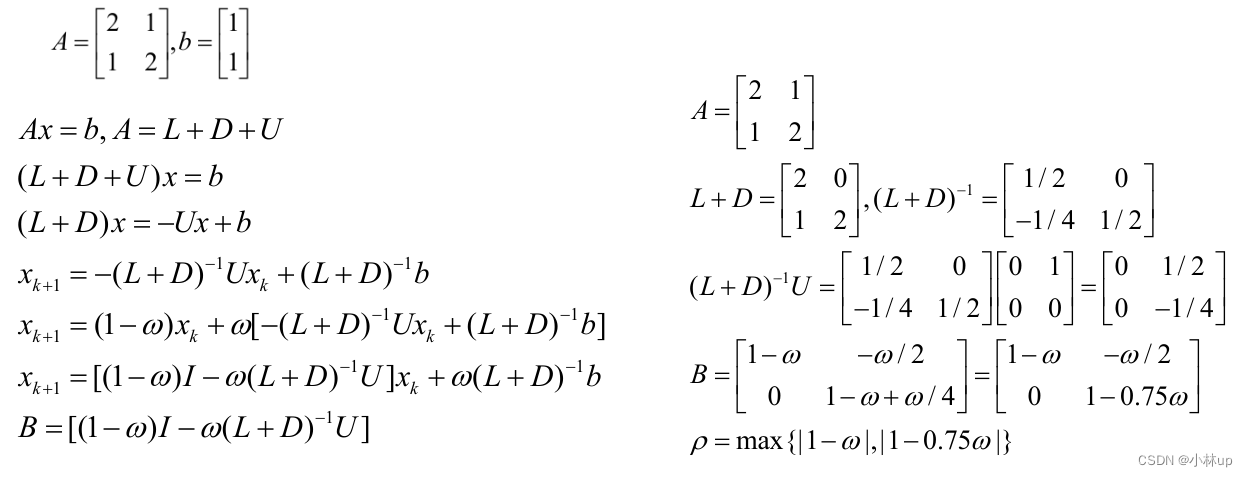
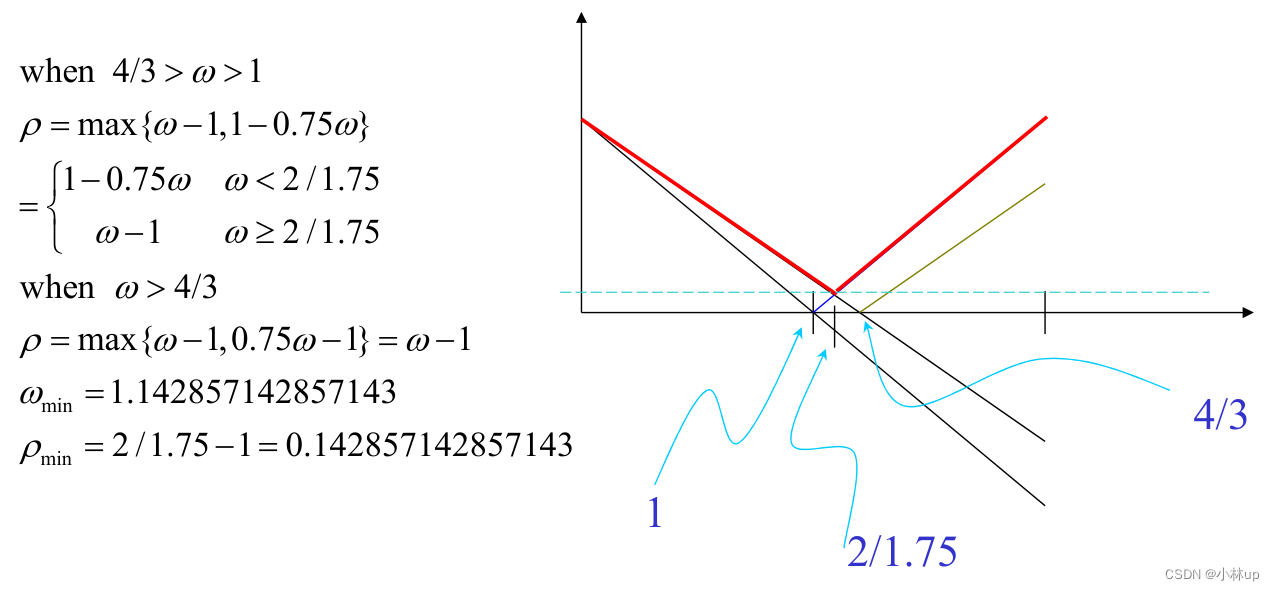
在SOR方法计算下,当系数矩阵 B B B的谱半径小于1但是非常接近1的时候,收敛速度较慢。
来看下面这个例子:
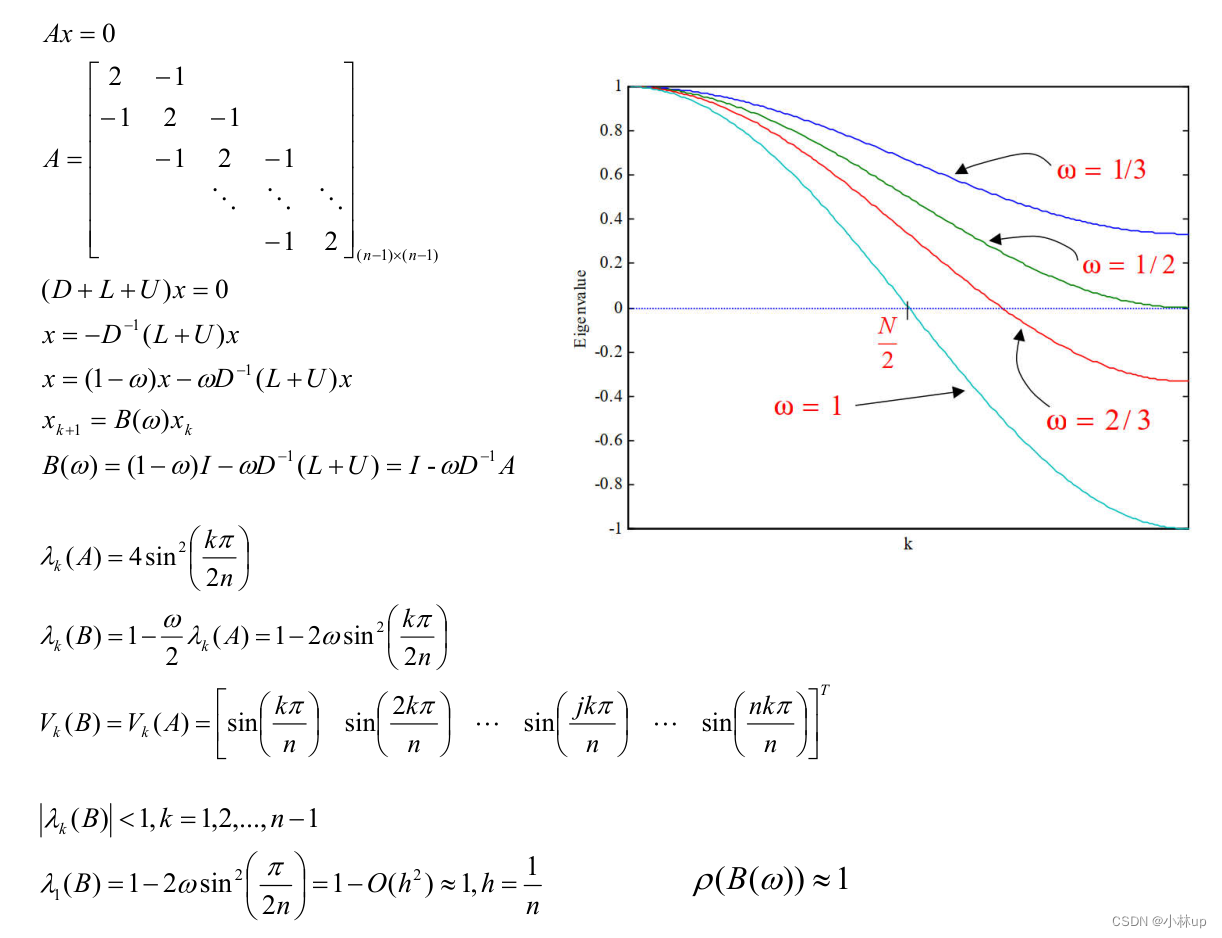
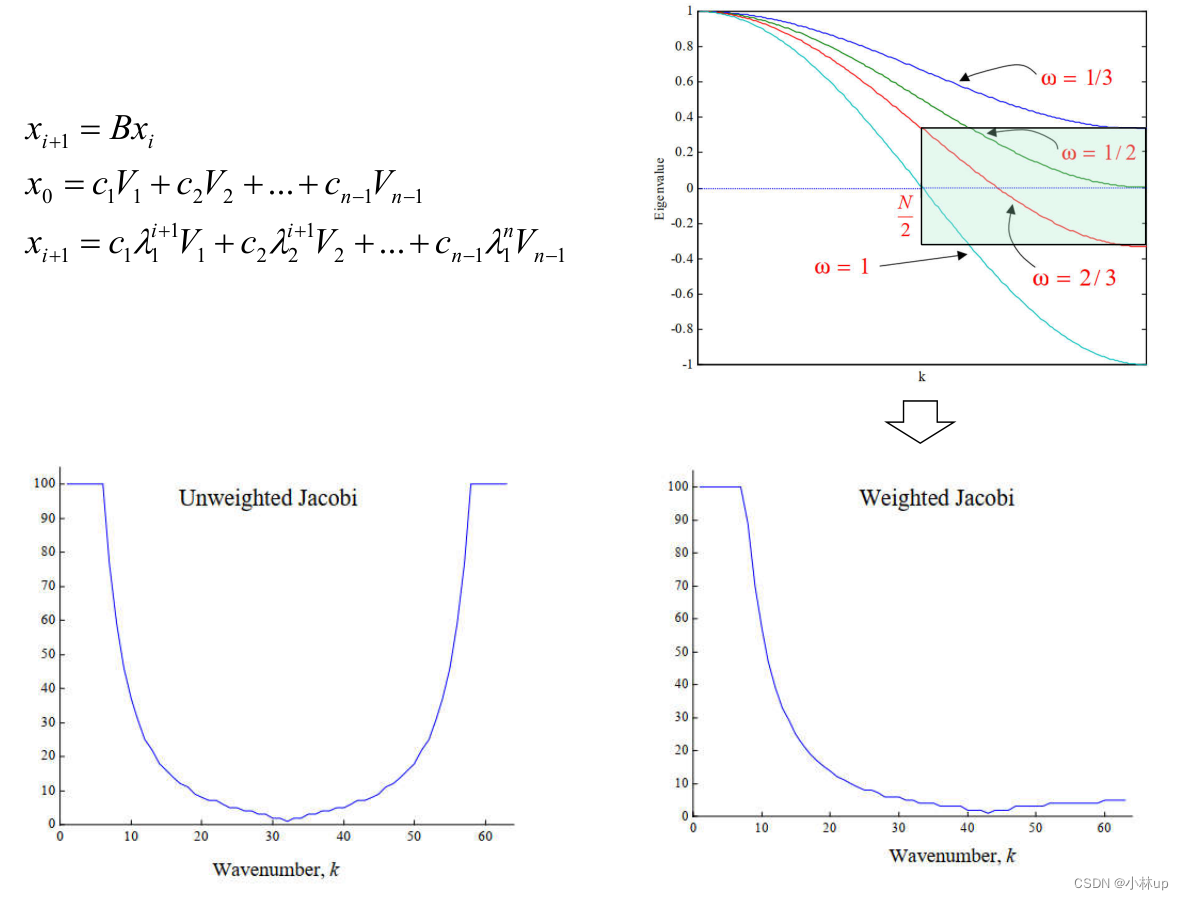
2.6 总结:Jacobi方法, Gauss-Seidel方法对比:

2.7 对称矩阵的Gauss-Seidel方法
对于一个对称矩阵 A A A
A = L + D + L T A=L+D+L^T A=L+D+LT
D D D是 A A A的对角线组成的对角阵, L L L是 A A A的下三角矩阵,由于对称, L T L^T LT是 A A A的上三角矩阵。
令 M = ( L + D ) D − 1 ( L + D ) T M = (L+D) D^{-1}(L+D)^{T} M=(L+D)D−1(L+D)T
x ( k + 1 ) = x ( k ) + M − 1 ( b − A x ( k ) ) = M − 1 b + M − 1 ( M − A ) x ( k ) = M − 1 b + M − 1 ( M − L − D − L T ) x ( k ) = M − 1 b + M − 1 ( ( L + D ) D − 1 ( L + D ) T − L − D − L T ) x ( k ) = M − 1 b + M − 1 ( L D − 1 L T + L D − 1 D T + D D − 1 L T + D D − 1 D T − L − D − L T ) x ( k ) = M − 1 b + M − 1 ( L D − 1 L T + L + L T + D T − L − D − L T ) x ( k ) = M − 1 b + M − 1 L D − 1 L T x ( k ) = M − 1 b + B x ( k ) \begin{aligned}x^{(k+1)}&=x^{(k)}+M^{-1}\left(b-A x^{(k)}\right)\\ &=M^{-1} b+M^{-1} (M-A)x^{(k)}\\ &=M^{-1} b+M^{-1} (M-L-D-L^{T})x^{(k)}\\ &=M^{-1} b+M^{-1} ( (L+D) D^{-1}(L+D)^{T}-L-D-L^{T})x^{(k)}\\ &=M^{-1} b+M^{-1} (L D^{-1} L^{T}+L D^{-1} D^{T}+D D^{-1} L^{T}+D D^{-1} D^{T}-L-D-L^{T} )x^{(k)}\\ &=M^{-1} b+M^{-1} (L D^{-1} L^{T}+L+L^{T}+D^T-L-D-L^{T} )x^{(k)}\\ &=M^{-1} b+M^{-1} L D^{-1} L^{T} x^{(k)}\\ &=M^{-1} b+B x^{(k)}\end{aligned} x(k+1)=x(k)+M−1(b−Ax(k))=M−1b+M−1(M−A)x(k)=M−1b+M−1(M−L−D−LT)x(k)=M−1b+M−1((L+D)D−1(L+D)T−L−D−LT)x(k)=M−1b+M−1(LD−1LT+LD−1DT+DD−1LT+DD−1DT−L−D−LT)x(k)=M−1b+M−1(LD−1LT+L+LT+DT−L−D−LT)x(k)=M−1b+M−1LD−1LTx(k)=M−1b+Bx(k)
式中的 B B B:
B = M − 1 L D − 1 L T \begin{aligned} B & = M^{-1} L D^{-1} L^{T} \end{aligned} B=M−1LD−1LT
2.8 Krylov方法(Krylov methods)
A x = b q ( λ ) = ∣ A − λ I ∣ = a 0 + a 1 λ + … + a n λ n = 0 q ( A ) = a 0 I + a 1 A + … + a n A n = 0 − 1 a 0 A ( a 1 I + … + a n A n − 1 ) = I A − 1 = − 1 a 0 ( a 1 I + … + a n A n − 1 ) x = A − 1 b = − 1 a 0 ( a 1 b + … + a n A n − 1 b ) ∈ span ( b , A b , A 2 b , … , A n − 1 b ) x ∗ = ∑ i c i A i b \begin{aligned} &A x = b \\ &q(\lambda) = |A-\lambda I| = a_{0}+a_{1} \lambda+\ldots+a_{n} \lambda^{n} & = 0 \\ &q(A) = a_{0} I+a_{1} A+\ldots+a_{n} A^{n} = 0 \\ &-\frac{1}{a_{0}} A\left(a_{1} I+\ldots+a_{n} A^{n-1}\right) = I \\ &A^{-1} = -\frac{1}{a_{0}}\left(a_{1} I+\ldots+a_{n} A^{n-1}\right) \\ &x = A^{-1} b = -\frac{1}{a_{0}}\left(a_{1} b+\ldots+a_{n} A^{n-1} b\right) \in \operatorname{span}\left(b, A b, A^{2} b, \ldots, A^{n-1} b\right) \\ &x^{*} = \sum_{i} c_{i} A^{i} b \end{aligned} Ax=bq(λ)=∣A−λI∣=a0+a1λ+…+anλnq(A)=a0I+a1A+…+anAn=0−a01A(a1I+…+anAn−1)=IA−1=−a01(a1I+…+anAn−1)x=A−1b=−a01(a1b+…+anAn−1b)∈span(b,Ab,A2b,…,An−1b)x∗=i∑ciAib=0
x ∗ x^* x∗的维数可小于 n n n!
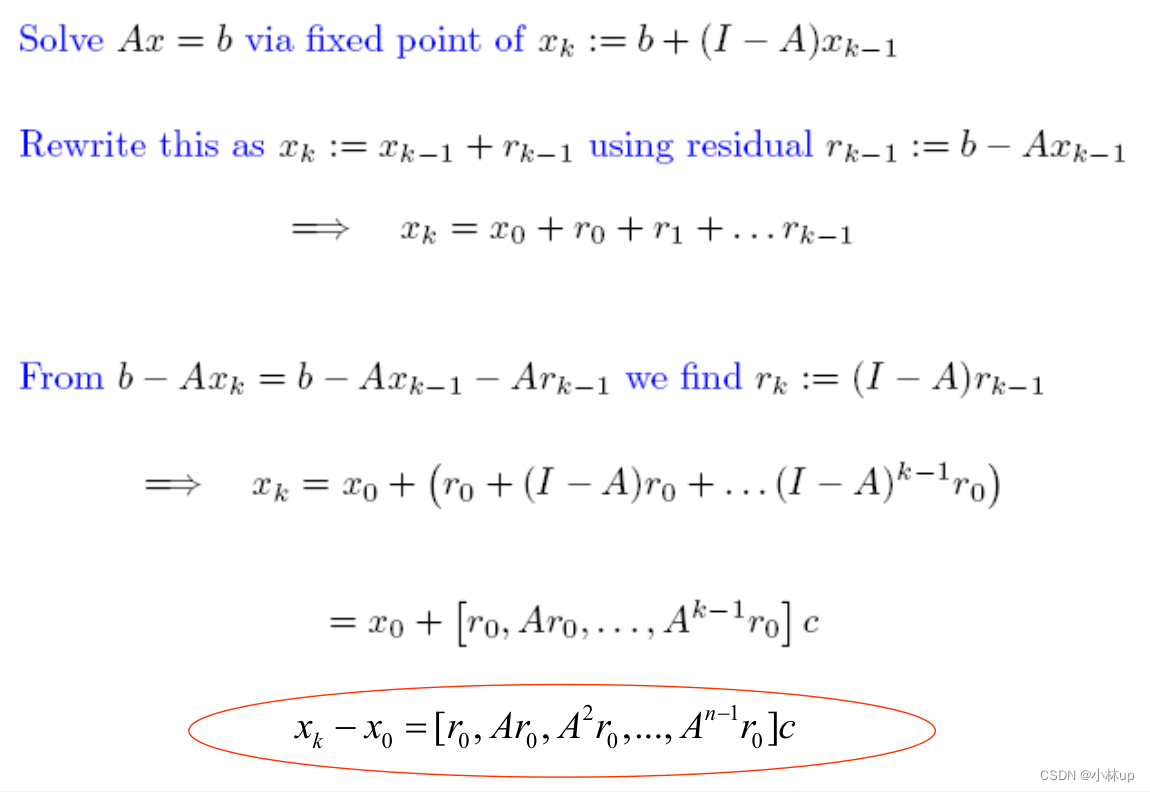
给定
x 0 = 0 x n = [ b , A b , A 2 b , … , A n − 1 b ] c ~ \begin{array}{l} x_{0}=0 \\ x_{n}=\left[b, A b, A^{2} b, \ldots, A^{n-1} b\right] \tilde{c} \end{array} x0=0xn=[b,Ab,A2b,…,An−1b]c~
x n x_{n} xn和 x ∗ x^* x∗落在一个空间,但可能不是一个很好的近似。
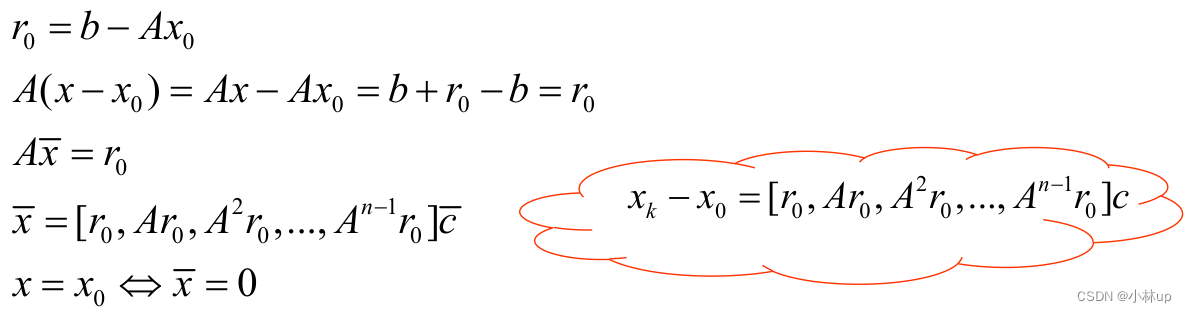

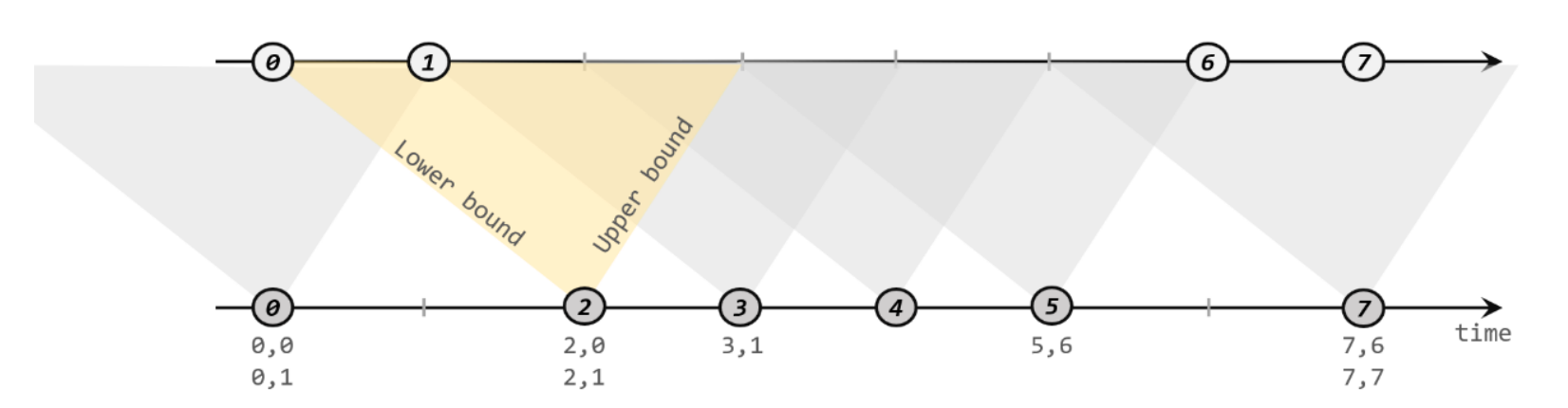
 (这个图有点不清楚,后面有空改一下)
(这个图有点不清楚,后面有空改一下)

原问题的解罗落在于一个Krylov 空间,其维数是
A
A
A的最小多项式的维度。因此,如果
A
A
A 的最小多项式的次数较低,则空间维数可以很小。
原来的空间张成向量 b , A b , A 2 b , ⋯ , A n − 1 b b,Ab,A^2b,\cdots,A^{n-1}b b,Ab,A2b,⋯,An−1b不正交转化为新的标准正交基 q q , q 2 , ⋯ , q n q_q,q_2,\cdots,q_n qq,q2,⋯,qn就有了下面的方法。
2.9 GMRES方法(Generalized Minimum Residual Method)

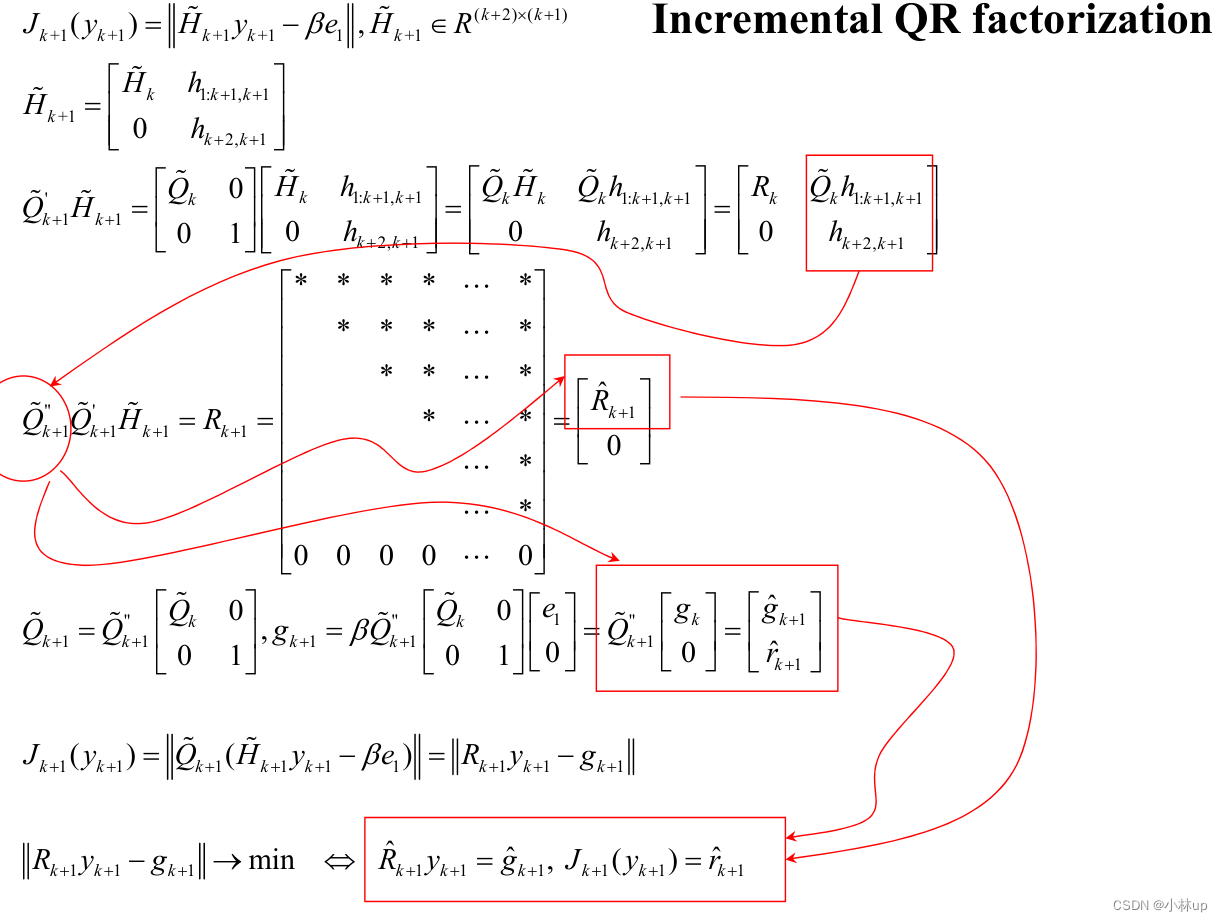
解释上面的第二步:
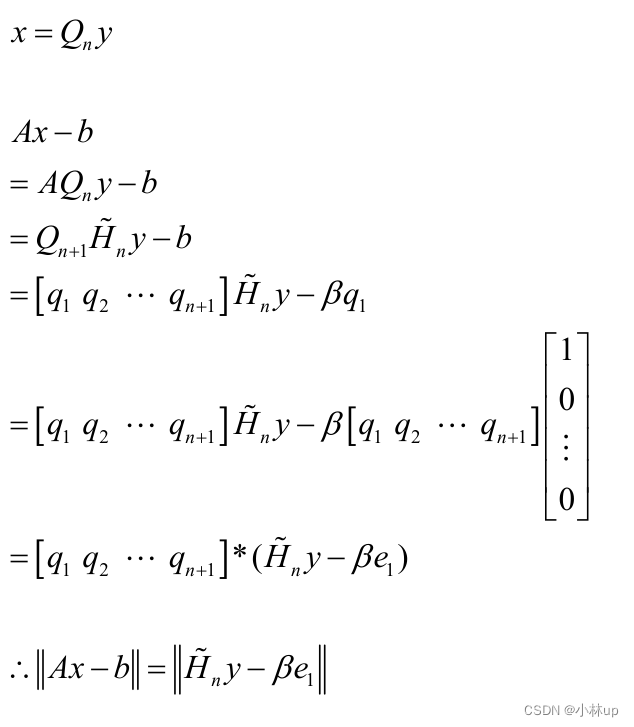

利用QR分解

3. 【线性方程组】基于优化的方法
- 若 A A A是一个对称正定矩阵,下面问题等价:
A x = b ⇔ min x 1 2 x T A x − b T x A x=b \Leftrightarrow \min _{x} \frac{1}{2} x^{T} A x-b^{T} x Ax=b⇔xmin21xTAx−bTx
- 若 A A A是一个大型稀疏方阵,下面问题等价:
A x = b ⇔ min x ∥ A x − b ∥ A x=b \Leftrightarrow \min _{x}\|A x-b\| Ax=b⇔xmin∥Ax−b∥
3.1 共轭梯度法(Conjugate gradient method【CG】)
两个向量 S 1 S_1 S1和 S 2 S_2 S2是共轭的,当它们满足 S 1 T A S 2 = 0 S_{1}^{\mathrm{T}} A S_{2}=0 S1TAS2=0
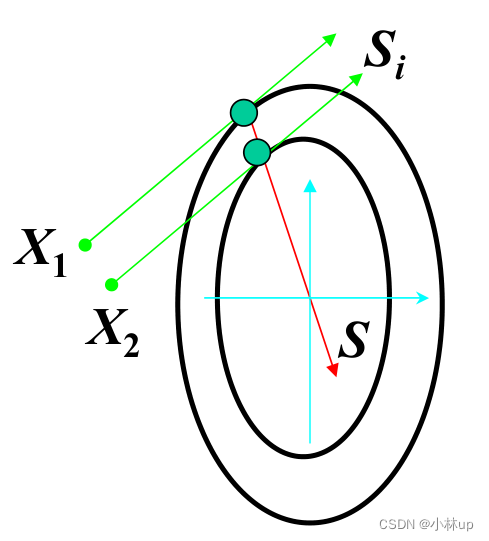
f
(
X
)
=
1
2
X
T
A
X
−
b
T
X
∇
f
(
X
)
=
A
X
−
b
ϕ
′
(
a
1
)
=
S
i
T
∇
f
(
X
1
+
a
1
S
i
)
=
S
i
T
(
A
X
(
1
)
−
b
)
=
0
X
(
1
)
=
X
1
+
a
1
S
i
ϕ
′
(
a
2
)
=
S
i
T
∇
f
(
X
2
+
a
2
S
i
)
=
S
i
T
(
A
X
(
2
)
−
b
)
=
0
X
(
2
)
=
X
2
+
a
2
S
i
S
i
T
A
(
X
(
2
)
−
X
(
1
)
)
=
S
i
T
A
S
=
0
\begin{aligned} &f(X) = \frac{1}{2} X^{T} A X-b^{T} X \\ &\nabla f(X) = A X-b \\ &\phi^{\prime}\left(a_{1}\right) = S_{i}^{T} \nabla f\left(X_{1}+a_{1} S_{i}\right) = S_{i}^{T}\left(A X^{(1)}-b\right) = 0 \quad X^{(1)}=X_{1}+a_{1} S_{i}\\ &\phi^{\prime}\left(a_{2}\right) = S_{i}^{T} \nabla f\left(X_{2}+a_{2} S_{i}\right) = S_{i}^{T}\left(A X^{(2)}-b\right) = 0 \quad X^{(2)}=X_{2}+a_{2} S_{i}\\ &S_{i}^{T} A\left(X^{(2)}-X^{(1)}\right) = S_{i}^{T} A S = 0 \end{aligned}
f(X)=21XTAX−bTX∇f(X)=AX−bϕ′(a1)=SiT∇f(X1+a1Si)=SiT(AX(1)−b)=0X(1)=X1+a1Siϕ′(a2)=SiT∇f(X2+a2Si)=SiT(AX(2)−b)=0X(2)=X2+a2SiSiTA(X(2)−X(1))=SiTAS=0
可以有限步数收敛!
算法流程:
1.
g
0
=
∇
f
(
x
0
)
,
d
0
=
−
g
0
;
2.
W
h
e
n
∣
g
k
∣
<
e
p
s
,
e
x
i
t
;
3.
a
k
=
arg
min
a
k
f
(
x
k
+
a
k
d
k
)
;
4.
g
k
+
1
=
∇
f
(
x
k
+
1
)
=
∇
f
(
x
k
+
a
k
d
k
)
;
5.
β
k
=
g
k
+
1
T
g
k
+
1
/
g
k
T
g
k
;
6.
d
k
+
1
=
−
g
k
+
1
+
β
k
d
k
;
7.
k
=
k
+
1
,
g
o
t
o
2.
\begin{aligned} &1. {g}_{0} = \nabla f\left({x}_{0}\right), {d}_{{0}} = -{g}_{0} ; \\&2. When \left|{g}_{{k}}\right|<{eps} , exit; \\&3. a_k = \mathop{\arg\min}\limits_{a_k} {f}\left({x}_{{k}}+a_{{k}} {d}_{{k}}\right) ; \\&4. g_{{k}+1} = \nabla f\left({x}_{{k}+1}\right) =\nabla f({x}_{{k}}+a_{{k}} {d}_{{k}}); \\&5. \beta_{{k}} = {g}_{{k}+1}^{{T}} {g}_{{k}+{1}} / {g}_{{k}}^{{T}} {g}_{{k}} ;\\ &6. d_{k+1} = -g_{k+1}+\beta_{k} d_{k} ;\\ &7. k = k+1 , go \,\,to\,\, 2 . \end{aligned}
1.g0=∇f(x0),d0=−g0;2.When∣gk∣<eps,exit;3.ak=akargminf(xk+akdk);4.gk+1=∇f(xk+1)=∇f(xk+akdk);5.βk=gk+1Tgk+1/gkTgk;6.dk+1=−gk+1+βkdk;7.k=k+1,goto2.
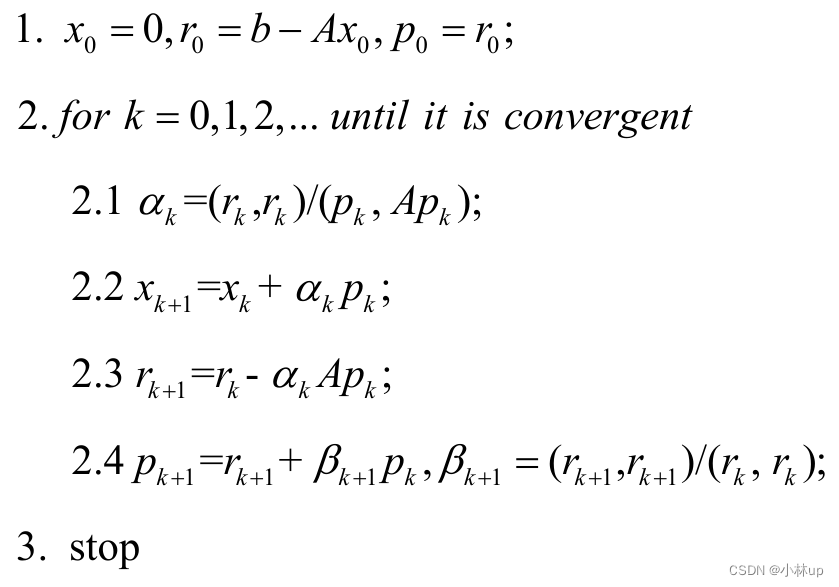
共轭梯度法(CG)特点:
①有限次收敛迭代
②计算复杂度
O
(
n
3
)
O(n^3)
O(n3),如果矩阵
A
A
A是一个对角矩阵,计算复杂度下降为
O
(
ω
n
2
)
O(\omega n^2)
O(ωn2)
3.2 共轭梯度法和其他算法的对比
共轭梯度法(CG) vs 高斯消元
①CG在所有有限步数之前可以得到足够精确的解
②CG保证稀疏性,即使
A
A
A不是对角阵。
共轭梯度法 vs 迭代方法
①CG保证收敛.
②收敛速度不同。
∥ x ( k + 1 ) − x ∗ ∥ A < C ∥ x ( k ) − x ∗ ∥ A , C = cond ( A ) − 1 cond ( A ) + 1 , ∥ x ∥ A = x T A x \left\|x^{(k+1)}-x^{*}\right\|_{A}<C\left\|x^{(k)}-x^{*}\right\|_{A}, C=\frac{\sqrt{\operatorname{cond}(A)}-1}{\sqrt{\operatorname{cond}(A)}+1},\|x\|_{A}=\sqrt{x^{T} A x} x(k+1)−x∗ A<C x(k)−x∗ A,C=cond(A)+1cond(A)−1,∥x∥A=xTAx
3.3 预条件共轭梯度法(Preconditioned conjugate gradient method)
在1.3我们讲到了条件数,预条件共轭梯度法就是想办法找到合适的 A ~ \tilde{A} A~降低条件数的大小,提高解的稳定性。
我们这样构造 A ~ \tilde{A} A~以及 x ~ \tilde{x} x~和 b ~ \tilde{b} b~
A ~ = C − 1 A C − T , x ~ = C T x , b ~ = C − 1 b \tilde{A}=C^{-1} A C^{-T}, \tilde{x}=C^{T} x,\tilde{b}=C^{-1} b A~=C−1AC−T,x~=CTx,b~=C−1b
于是有:
A
x
=
b
⇔
A
~
x
~
=
b
~
A x=b \Leftrightarrow \tilde{A} \tilde{x}=\tilde{b}
Ax=b⇔A~x~=b~
我们可以验证:
c o n d 2 ( A ~ ) < c o n d 2 ( A ) c o n d 2 ( A ) = ∣ λ max ∣ ∣ λ min ∣ {cond}_{2}(\tilde A)<{cond}_{2}(A)\quad {cond}_{2}(A)=\frac{\left|\lambda_{\max }\right|}{\left|\lambda_{\min }\right|} cond2(A~)<cond2(A)cond2(A)=∣λmin∣∣λmax∣
- 按照下面的方式取定 C C C,条件数变小了【这一块没写清楚,回头再写写补坑】
C − 1 = D − 1 / 2 , D = diag ( a 11 , a 22 , … , a n n ) , A = ( a i j ) n × n C^{-1}=D^{-1 / 2}, D=\operatorname{diag}\left(a_{11}, a_{22}, \ldots, a_{n n}\right), A=\left(a_{i j}\right)_{n \times n} C−1=D−1/2,D=diag(a11,a22,…,ann),A=(aij)n×n
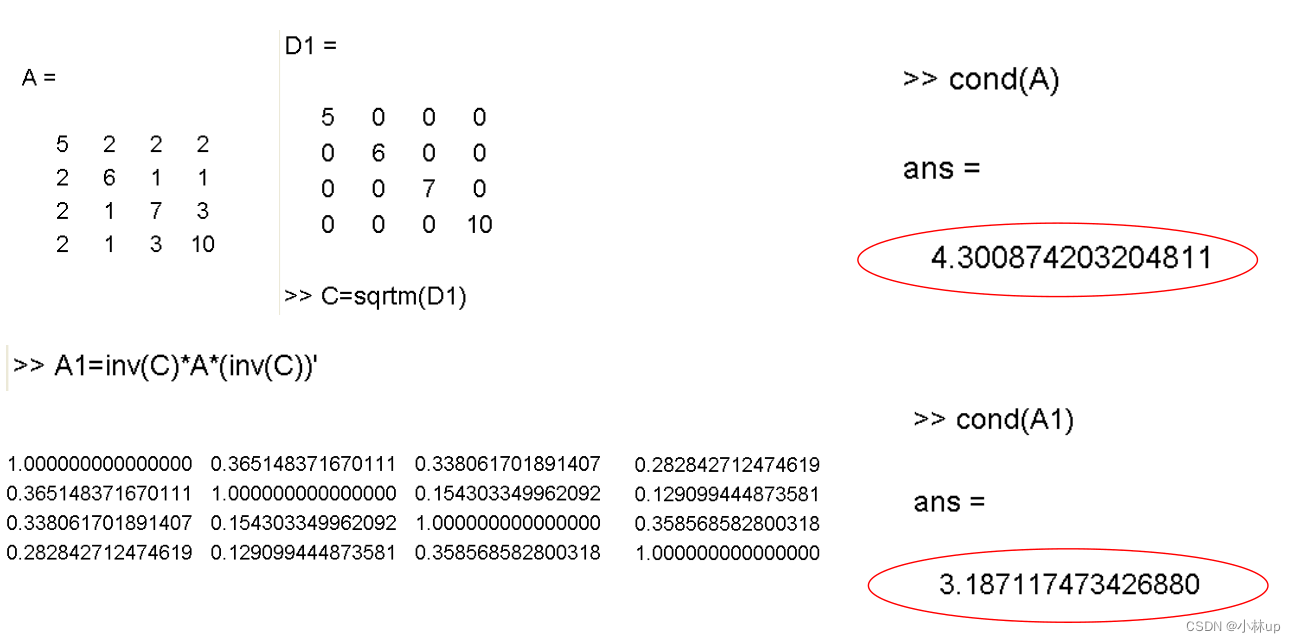
2. 按照下面的方式取定
C
C
C,条件数变小了
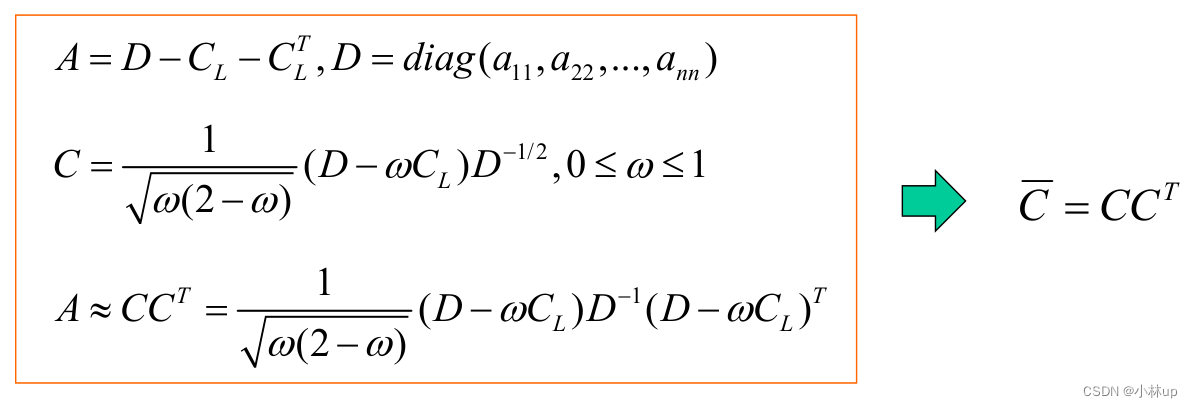
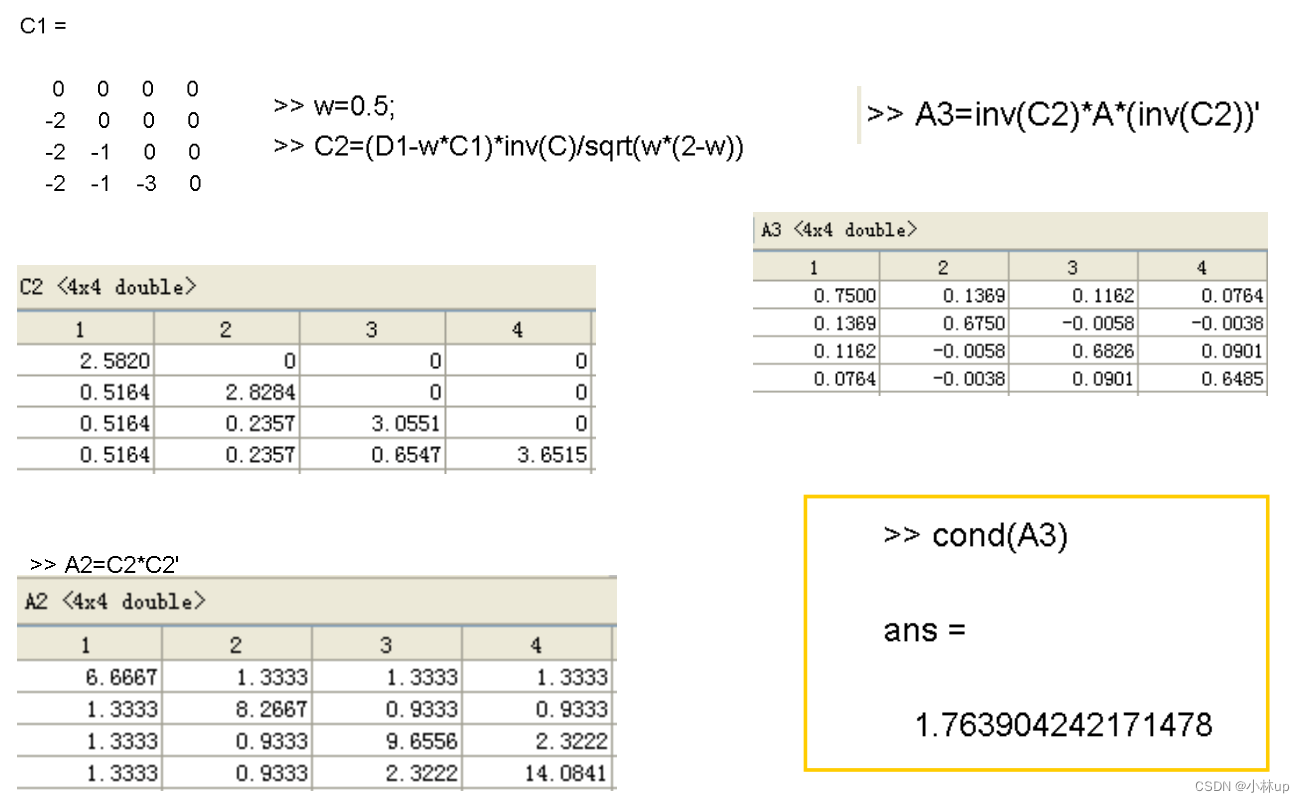
预条件共轭梯度法算法流程:
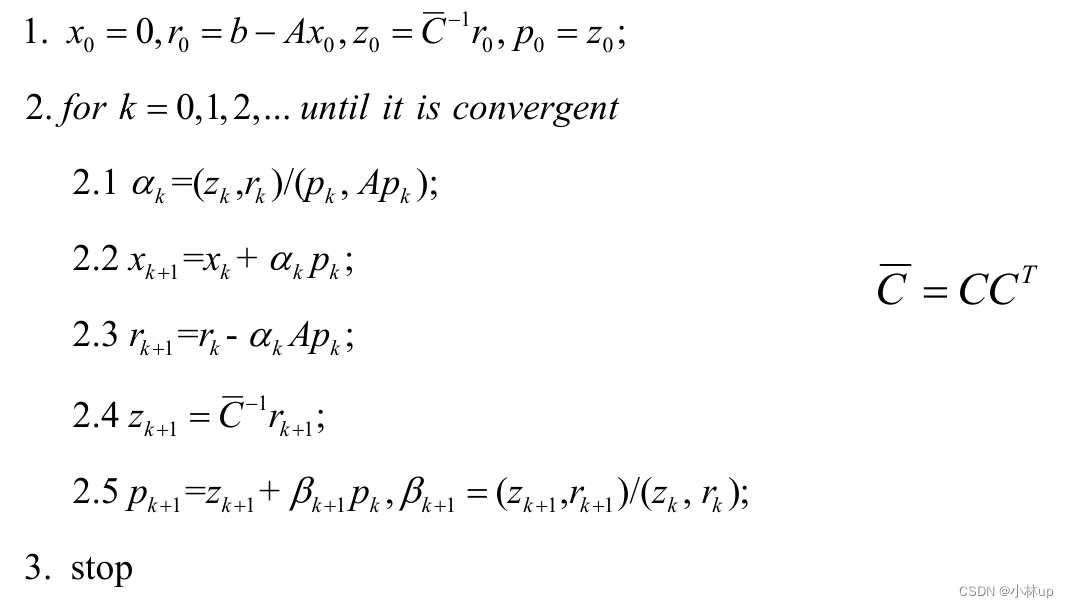
4. 【非线性方程组】Jacobian矩阵、Newton迭代法、不动点迭代法、Seidel迭代法
4.1 Jacobian矩阵
针对一个非线性方程组,可能有无穷多解。利用Jacobian矩阵迭代线性化处理变为求解线性方程组。
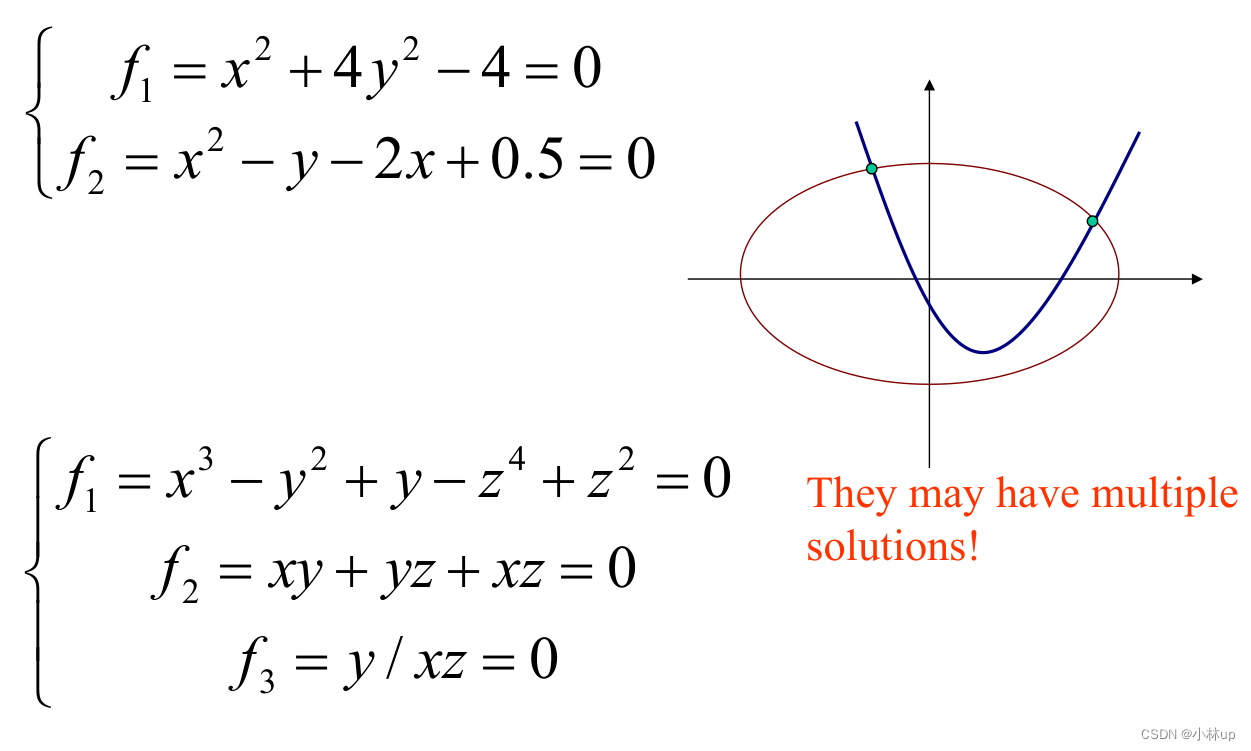


利用Jacobian矩阵引出Newton方法:
4.2 Newton迭代法

算法流程

Jacobian矩阵的问题
①出现奇异,内部元素分母为0或矩阵的秩为0
②收敛阶数降低
③有不确定性
4.3 不动点迭代法

假设
g
i
g_i
gi 的偏导数在包含不动点
(
p
,
q
,
r
)
(p,q,r)
(p,q,r)的一个区域上是连续的。如果选择的起点足够接近定点,并且
∣
∂
g
1
∂
x
(
p
,
q
,
r
)
∣
+
∣
∂
g
1
∂
y
(
p
,
q
,
r
)
∣
+
∣
∂
g
1
∂
z
(
p
,
q
,
r
)
∣
<
1
,
∣
∂
g
2
∂
x
(
p
,
q
,
r
)
∣
+
∣
∂
g
2
∂
y
(
p
,
q
,
r
)
∣
+
∣
∂
g
2
∂
z
(
p
,
q
,
r
)
∣
<
1
,
∣
∂
g
3
∂
x
(
p
,
q
,
r
)
∣
+
∣
∂
g
3
∂
y
(
p
,
q
,
r
)
∣
+
∣
∂
g
3
∂
z
(
p
,
q
,
r
)
∣
<
1
,
\begin{array}{l} \left|\frac{\partial g_{1}}{\partial x}(p, q, r)\right|+\left|\frac{\partial g_{1}}{\partial y}(p, q, r)\right|+\left|\frac{\partial g_{1}}{\partial z}(p, q, r)\right|<1, \\ \left|\frac{\partial g_{2}}{\partial x}(p, q, r)\right|+\left|\frac{\partial g_{2}}{\partial y}(p, q, r)\right|+\left|\frac{\partial g_{2}}{\partial z}(p, q, r)\right|<1, \\ \left|\frac{\partial g_{3}}{\partial x}(p, q, r)\right|+\left|\frac{\partial g_{3}}{\partial y}(p, q, r)\right|+\left|\frac{\partial g_{3}}{\partial z}(p, q, r)\right|<1, \end{array}
∂x∂g1(p,q,r)
+
∂y∂g1(p,q,r)
+
∂z∂g1(p,q,r)
<1,
∂x∂g2(p,q,r)
+
∂y∂g2(p,q,r)
+
∂z∂g2(p,q,r)
<1,
∂x∂g3(p,q,r)
+
∂y∂g3(p,q,r)
+
∂z∂g3(p,q,r)
<1,
这意味着
ρ
(
J
)
≤
∥
J
∥
∞
<
1
\rho(J) \leq\|J\|_{\infty}<1
ρ(J)≤∥J∥∞<1。
那么不动点迭代收敛到定点。
4.4 Seidel迭代法
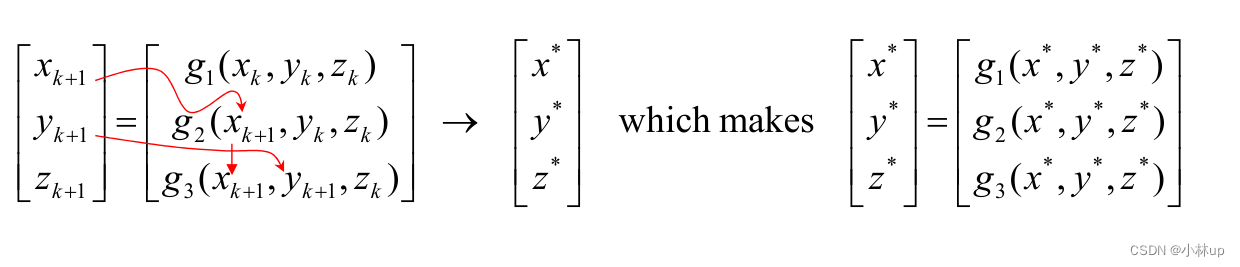
5. Matlab相关函数