1.ID3算法
ID3算法利用信息增益进行特征的选择进行树的构建。信息熵的取值范围为0~1,值越大,越不纯,相反值越小,代表集合纯度越高。信息增益反映的是给定条件后不确定性减少的程度。每一次对决策树进行分叉选取属性的时候,我们会选取信息增益最高的属性来作为分裂属性,只有这样,决策树的不纯度才会降低的越快。
2.信息增益
它定义为一个特征能够为分类系统带来多少信息,带来的信息越多,说明该特征越重要,相应的信息增益也就越大。 在决策树中,通过一个特征将数据集划分,划分数据集的先后信息发生的变化称为信息增益,计算出每个特征值划分数据集获得的信息增益,获取信息增益最高的特征就是最好的选择。信息增益通俗来说就是信息选择的特征。信息增益代表了在一个条件下,信息复杂度(不确定性)减少的程度。信息增益与信息熵和条件熵有关,信息熵、条件熵、信息增益的具体含义如下。信息熵是消除不确定性所需信息量的度量,也即未知事件可能含有的信息量。事件越不确定,信息熵就越高
2-1 信息熵
物理学上,熵 Entropy是“混乱”程度的量度。系统越有序,熵值越低;系统越混乱或者分散,熵值越高。
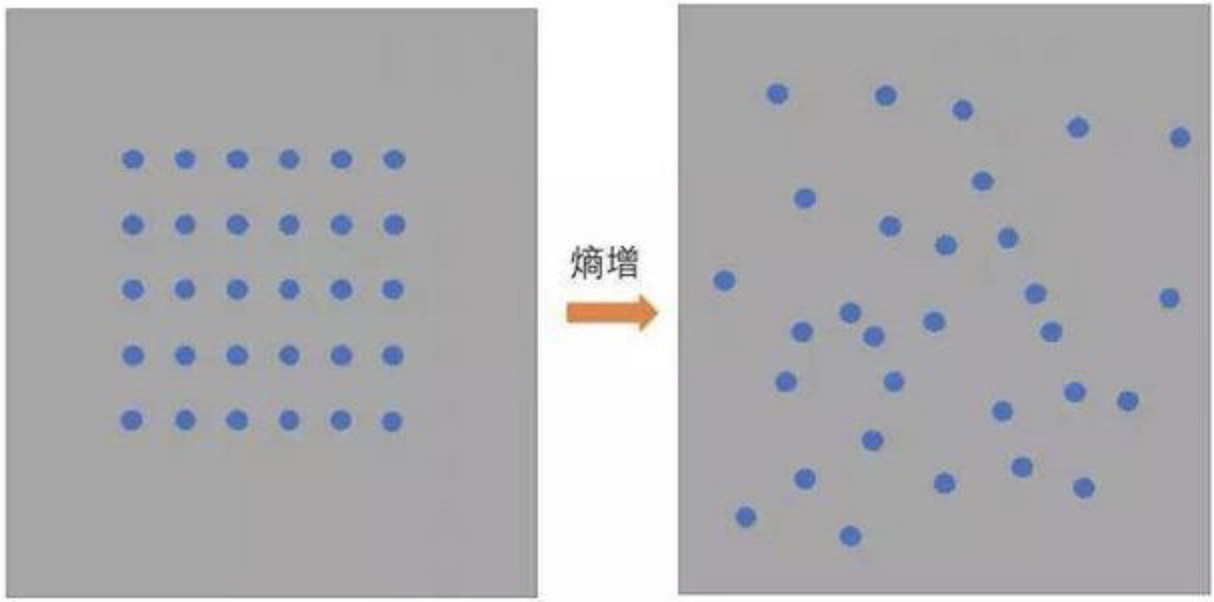
信息熵:表示随机变量的不确定性。熵为信息的期望值,即计算所有类别所有可能包含的信息期望值,通过以下公式得到。其中n是分类的数目。p(i)为该分类的概率。
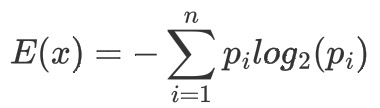
2-2 条件熵
条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵H(Y|X)。在X给定的条件下,Y的条件概率分布的熵对X 的数学期望(度量在定情况下,随机变量的不确定性)。
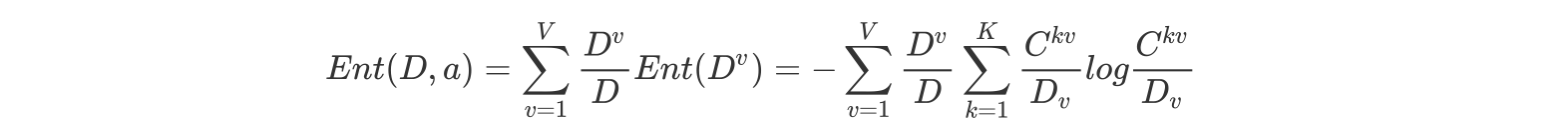
2-3 信息增益
信息增益:熵 - 条件熵。表示在一个条件下,信息不确定性减少的程度。对于待划分的数据集D,其 entroy(前)是一定的,但是划分之后的熵 entroy(后)是不定的,entroy(后)越小说明使用此特征划分得到的子集的不确定性越小(也就是纯度越高),因此 entroy(前) - entroy(后)差异越大,说明使用当前特征划分数据集D的话,其纯度上升的更快。
2-4 案例
如下图,第一列为论坛号码,第二列为性别,第三列为活跃度,最后一列用户是否流失。我们要解决一个问题:性别和活跃度两个特征,哪个对用户流失影响更大?
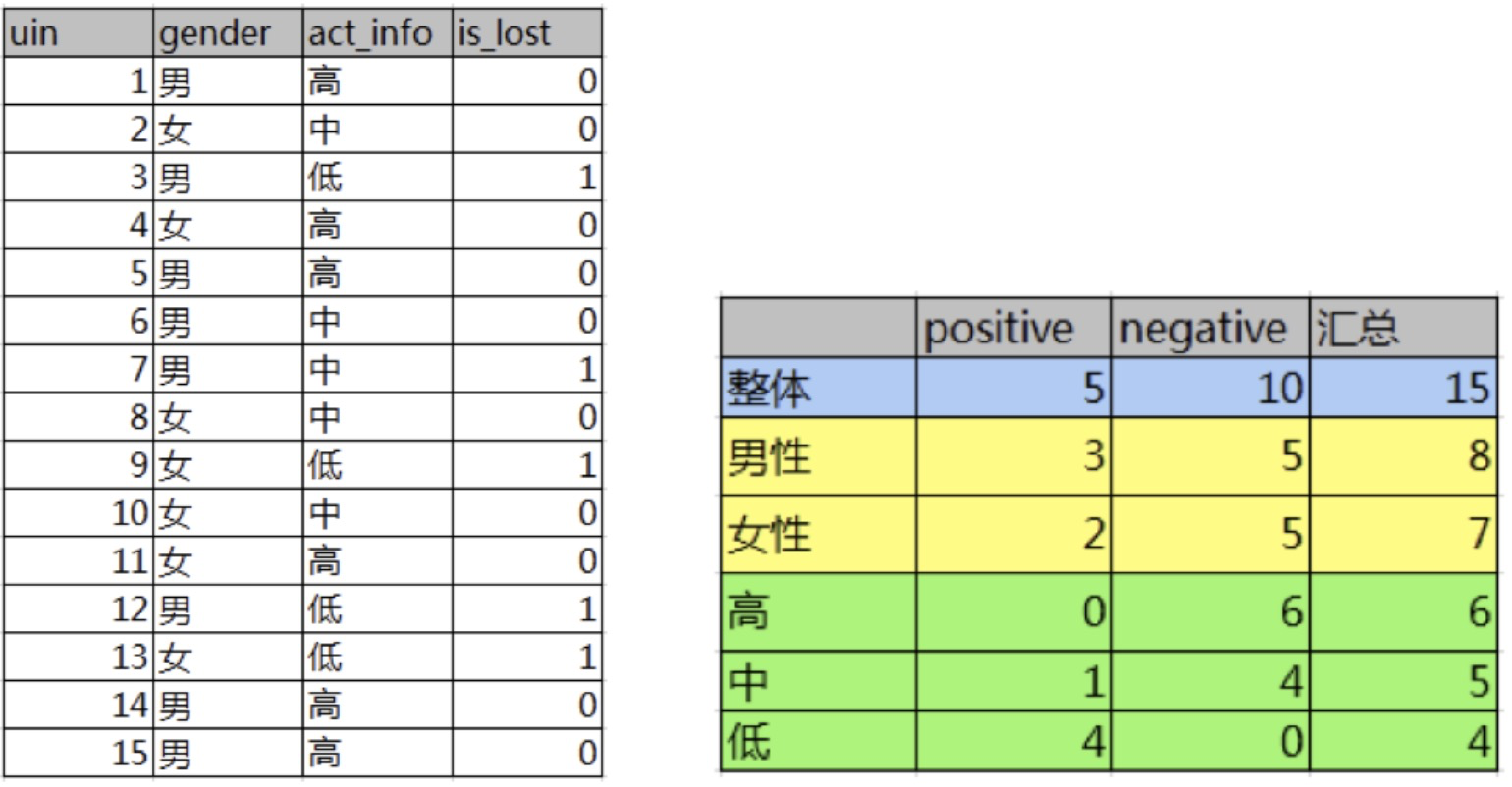
其中Positive为正样本(已流失),Negative为负样本(未流失),下面的数值为不同划分下对应的人数。
a.计算类别信息熵 整体熵
b.计算性别属性的信息熵(a="性别")
c.计算性别的信息增益(a="性别")
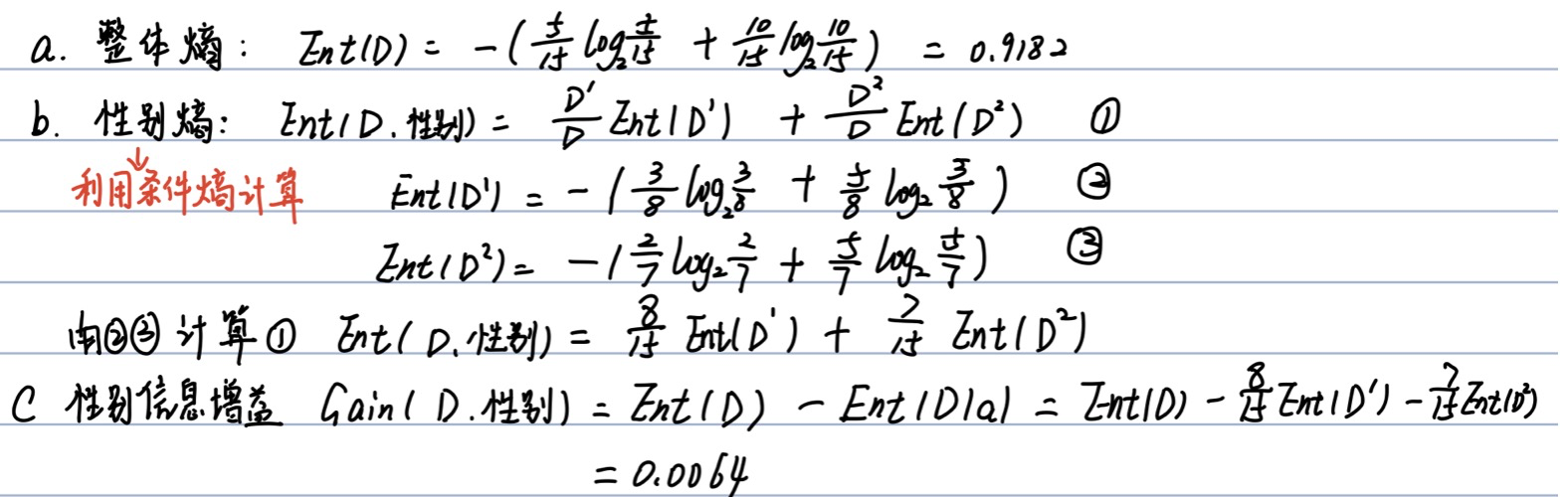
b.计算活跃度属性的信息熵(a="活跃度")
c.计算活跃度的信息增益(a="活跃度")

结论:活跃度的信息增益比性别的信息增益大,也就是说,活跃度对用户流失的影响比性 别大。在做特征选择或者数据分析的时候,应该重点考察活跃度这一指标。
3.总结
信息增益可以很好的度量特征的信息量,但在某些情况下存在一些弊端。对可取值数目较多的属性有所偏好。因为信息增益反映的是给定一个条件以后不确定性减少的程度,必然是分得越细的数据集确定性更高,也就是条件熵越小,信息增益越大。信息增益偏向取值较多的特征。
Reference:
1.https://www.cnblogs.com/yuyingblogs/p/15319571.html