根据网络图的基本概念和原则绘制出网络图之后,我们可以计算网络图中有关的时间参数,主要目的是找出关键路线,为网络计划的优化、调整和执行提供明确的时间概念。如下图中从始点①到终点⑧共有4条路线,可以分别计算出每条路线所需的总工时。
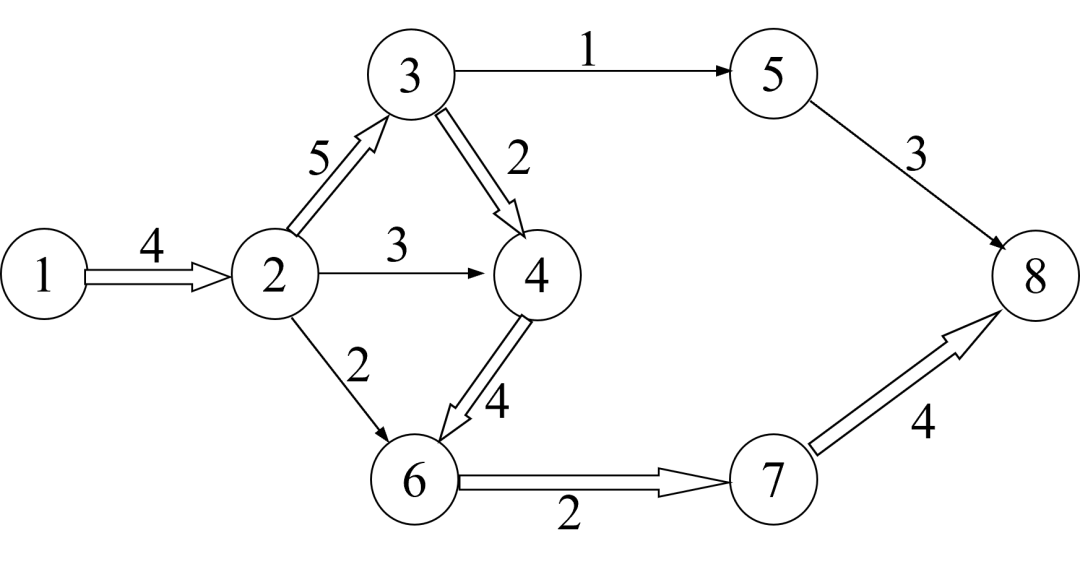
这4条路线分别为:
①→②→③→⑤→⑧
4+5+1+3=13(周)
①→②→④→⑥→⑦→⑧
4+3+4+2+4=17(周)
①→②→⑥→⑦→⑧
4+2+2+4=12(周)
①→②→③→④→⑥→⑦→⑧
4+5+2+4+2+4=21(周)
根据上述几个公式,我们不难看出①→②→③→④→⑥→⑦→⑧所需时间最长,它表明整个任务的总完工期为21周。这条线上的工作,若有一个延迟一周,整个工期就要推迟一周;若某一工作能提前一周,整个任务就可以提前一周完成。而不在这条路上的工作对总工期则没有这种直接影响的关系,如工作②→⑥,可以在①→②工作开始后四周就开始,也可以推迟到l0周、13周(最晚13周)后再开工,都不影响总完工期。
通常把网络图中需时最长的路叫作关键路,在图中用双线箭头⇒画出,把关键路线上的工作称为关键工作。要想使任务按期或者提前完工,就要在关键路线的关键工作上想办法。网络图的关键路线可以通过时间参数的计算求得。
二、时间参数
网络图的时间参数包括工作所需时间、事项最早、最迟时间、工作的最早、最迟时间及时差等。进行时间参数计算不仅可以得到关键路线,确定和控制整个任务在正常的进度下的最早完工期,而且在掌握非关键工作的基础上可进行人、财、物等资源的合理安排,进行网络计划的优化。
1. 工作时间t(i,j)✦
工作(i,j)的所需工时可记为t(i,j),有两种确定方法。
(1)确定型
在具备工时定额和劳动定额的任务中,工作的工时t(i,j)可以用这些定额资料确定。有些工作虽无定额可查,但有有关工作的统计资料,也可利用统计资料通过分析来确定工作的工时。
(2)概率型
对于开发性试制性的任务,往往不具备可用的定额资料,难以准确估计工作所需工时,可以采用三点时间估计法来确定工作的工时。这种方法对每道工作先要作出三种情况的时间估计:
①a,最快可能完成时间(最乐观时间);
②m,最可能完成时间;
③b,最慢可能完成时间(最悲观时间)。
利用上述3个时间,可估计每道工作的期望工时:

方差:

2. 事项时间参数✦
(1)事项的最早时间
事项j的最早时间用tE(j)表示,它表明以它为始点的各工作最早可能开始的时间,也表示以它为终点的各工作的最早可能完成时间(相同),它等于从始点事项到该事项的最长路线上所有工作的工时总和。事项最早时间可用下列递推公式,按照事项编号从小到大的顺序逐个计算。
设总开工事项编号为①:

式中tE(i)表示与事项j相邻的各紧前事项的最早时间。
设终点事项编号为n,则终点事项的最早时间显然就是整个工程的总最早完工期,即:tE(n)为总最早完工期。
(2)事项的最迟时间
事项i的最迟时间用tL(i)表示,它表明在不影响任务总工期条件下,以它为始点的工作的最迟必须开始时间,或以它为终点的各工作的最迟必须完成时间。由于一般情况下,我们都把任务的最早完工时间作为任务的总工期,所以事项最迟时间的计算公式为:

其中,tL(i)表示与事项i相邻的各紧后事项的最迟时间。公式(2)也是递推公式,但与(1)式相反,是从终点事项开始,按编号由大至小的顺序逐个由后向前计算。
3. 工作的时间参数✦
(1)工作的最早可能开工时间与工作的最早可能完工时间
一个工作(i,j)的最早可能开工时间用tES(i,j)表示。任何一件工作都必须在其所有紧前工作全部完工后才能开始。工作(i,j)的最早可能完工时间用tEF(i,j)表示。它表示工作按最早开工时间开始所能达到的完工时间。它们的计算公式为:

这组公式也是递推公式。即所有从总开工事项出发的工作(1,j),其最早可能开工时间为零;任一工作(i,j)的最早开工时间要由它的所有紧前工作(k,i)的最早开工时间决定;工作(i,j)的最早完工时间显然等于其最早开工时间与工时之和。
(2)工作的最迟必须开工时间与工作的最迟必须完工时间
工作(i,j)的最迟必须开工时间用tLS(i,j)表示。它表示工作(i,j)在不影响整个任务如期完成的前提下,必须开始的最晚时间。工作(i,j)的最迟必须完工时间用tLF(i,j)表示。它表示工作(i,j)按最迟时间开工,所能达到的完工时间。其的计算公式为:
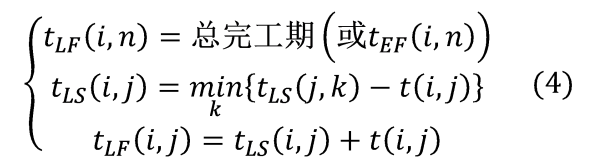
这组公式是按工作的最迟必须开工时间由终点向始点逐个递推的公式。凡是进入总完工事项n的工作(i,n),其最迟完工时间必须等于预定总工期或这个工作的最早可能完工时间。任一工作(i,j)的最迟必须开工时间由它的所有紧后工作(j,k)的最迟开工时间确定。而工作(i,j)的最迟完工时间显然等于本工作的最迟开工时间加工时。
由于任一个事项i(除去始点事项和终点事项),既表示某些工作的开始又表示某些工作的结束;所以从事项与工作的关系考虑,有关工作的时间参数也可以通过事项的时间参数来计算。
如工作(i,j)的最早可能开工时间tES(i,j)就等于事项i的最早时间tE(i)。工作(i,j)的最迟必须完工时间等于事项j的最迟时间。
4. 时差✦
工作的时差又叫工作的机动时间或富裕时间,常用的时差有两种。
(1)工作的总时差
在不影响任务总工期的条件下,某工作(i,j)可以延迟其开工时间的最大幅度,叫做该工作的总时差,用R(i,j)表示。其计算公式为:
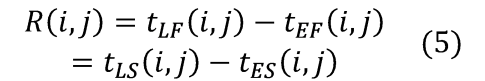
(2)工作的单时差
工作的单时差是指在不影响紧后工作的最早开工时间条件下,此工作可以延迟其开工时间的最大幅度,用r(i,j)表示。其计算公式为:
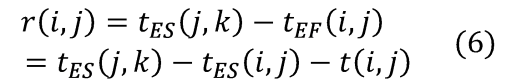
即单时差等于其紧后工作的最早开工时间与本工作的最早完工时间之差。
(3)工作总时差和单时差的区别与联系
工作总时差和单时差的区别与联系可以通过下图来说明。在图中,工作b与工作c同为工作a的紧后工作。可以看出,工作a的单时差不影响紧后工作的最早开工时间,而其总时差却不仅包括本工作的单时差,而且包括了工作b,c的时差,使工作c失去了部分时差而工作b失去了全部自由机动时间。所以占用一道工序的总时差虽然不影响整个任务的最短工期,却有可能使其紧后工作失去自由机动的余地。

■ 网络中最长的路线就决定了完成整个工程所需的最少时间,这条路线称为关键路线。
■ 总时差为0的工序为关键工序。
三、确定型网络图时间参数计算
网络图时间参数的计算方法很多,如图上计算法、表上计算法、矩阵法以及使用计算机计算等。下面结合一道例题分别介绍图上计算法和表上计算法。
例 题
根据下面的网络图找出关键路线。

Part.1
时间参数的图上计算法
图上计算法的具体步骤如下:
(1)计算事项的时间参数
①事项最早时间计算。事项的最早时间从总开工事项①开始,利用公式(1),在图上由编号小到大逐个计算。
tE(1)=0
tE(2)=0+4=4
tE(3)=4+6=10
tE(4)=max{4+3,10+8}=18
…
tE(10)=32

计算原则
■ 所有进到该事项的箭尾最早时间加箭杆上工作时间,取最大。
②事项最迟时间计算。事项的最迟时间从总完工事项⑩开始,利用公式(2),在图上由编号大到小逐个计算。当任务给定完工期限时,事项⑩的最迟时间就等于规定期限,否则就等于刚计算出的事项⑩的最早时间32。
tL(10)=32
tL(9)=32-1=31
tL(8)=31-5=26
tL(7)=min{31-8,26-2}=23
…
tL(1)=4-4=0

计算原则
■ 所有离开该事项的箭头最迟时间减箭杆上工作时间,取最小。
(2)工作时间参数的计算
与计算事项的时间参数类似,先用式(3)从始点开始,逐个计算工作的最早可能开工时间,标入箭杆上方的菱形方框的上半部。然后从终点由后向前按式(4)逐个计算工作最迟必须开工时间,填入菱形方框的下半部。
工作的最早可能开工时间和工作的最迟必须开工时间,这两个一旦算出,那么工作的最早可能完工时间和工作的最迟必须完工时间将很容易算得,下面仅举例算出工作的最早可能开工时间和工作的最迟必须开工时间,如下图所示:

计算原则
■ 最早可能开工时间:所有紧前工作的最早开始时间加该工作时间,取最大。
■ 最迟必须开工时间:所有紧后工作的最晚开始时间减该工作时间,取最小。
(3)计算总时差和单时差
工作的总时差就是下图中的下三角减去上三角,标记在图中【】处,单时差利用式(6)计算,标记在图中()处。

由关键路线的意义可知,这条线在时间上没有回旋余地,即每个关键工作应满足“最早开工时间等于最迟必须开工时间”的条件,而非关键工作则有富裕时间。所以总时差为零的工作链就是关键路线。
以总时差为零为依据检查各工作的总时差,得出关键路线如下图所示。
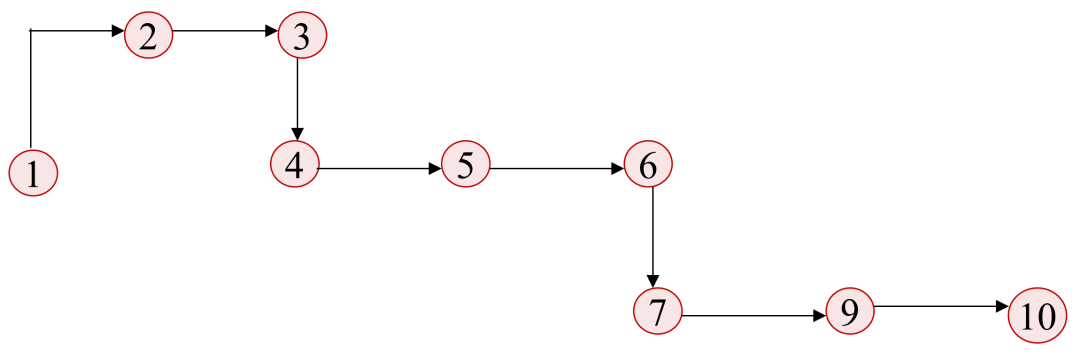
Part.2
时间参数的表上计算法
在网络图上直接计算时间参数,方法简便直观。但是当工作数目多,图形复杂时容易遗漏和出错,故常常采用表格法。表上计算法的具体步骤如下:
(1)列出计算用表
如下表的表头,注意工作的排列应严格按照箭尾事项编号由小到大的顺序排列,箭尾事项相同的工作,按其箭头事项由小到大排列。将已知各工作的工时(第3列)填入表中:

(2)计算工作的最早开工时间和最早完工时间
利用公式(3)首先计算出最早开工时间,再用最早开工时间加上工作时间求得最早完工时间,按照由上至下的顺序逐个计算填入表格中的第4列、第5列。
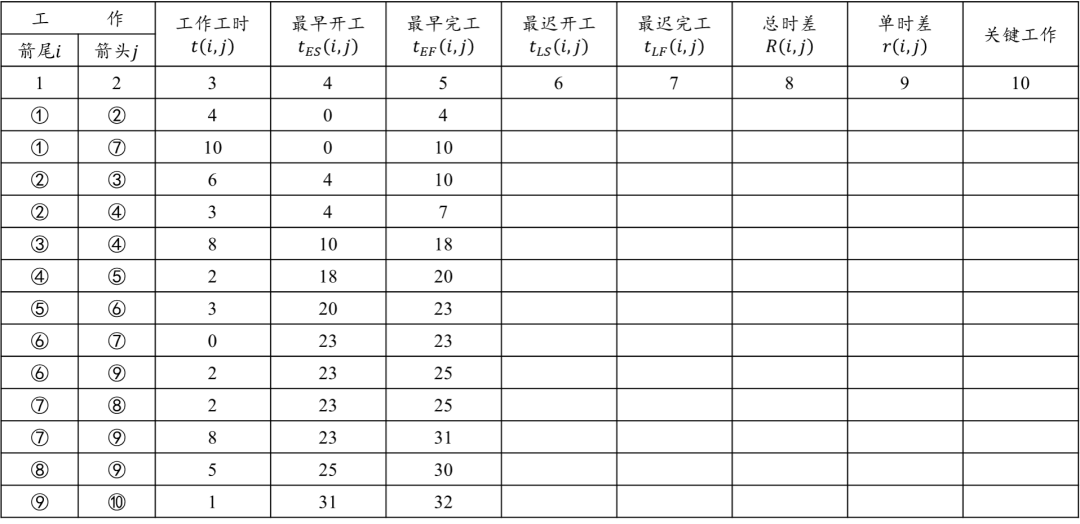
(3)计算并填写工作的最迟开工和最迟完工时间
即表中第6列、第7列,计算和填写顺序是由下至上,利用公式(4)首先计算出最迟完工时间,然后用最迟完工时间减去工作时间得到最迟开工时间。

(4)计算总时差和单时差
第8列总时差可由各工作第6列与第4列上的数相减求得即用公式(5),也可以由第7列与第5列相减求得。第9列单时差是用公式(6)由紧后工作的第4列与该项工作第5列相应数字相减得到。按总时差为0选出关键工作写入第10列,得到关键路线,最终结果如下图。
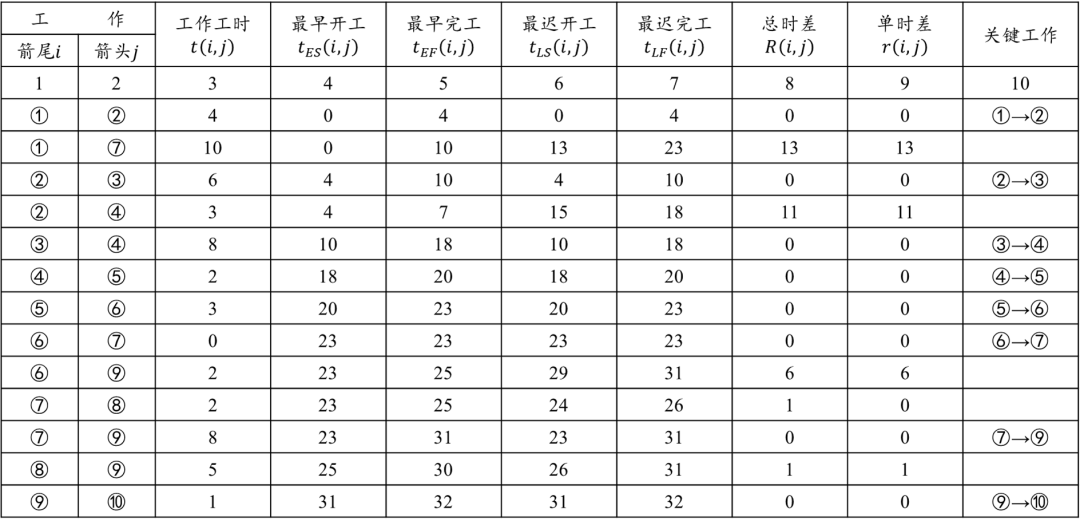
四、概率型网络图时间参数计算
对于概率型网络图,当求出每道工作的平均期望工时t和方差σ2后,就可以同确定型网络图一样,计算有关时间参数及总完工期TZ。由于它们的工作工时本身包含着随机因素,所以整个任务的总完工期也是个期望工期。它是关键路线上各道工作的平均工时之和TZ =Σt,所以总完工期的方差就是关键路上所有工序的方差之和Σσ2。若工作足够多,每一工作的工时对整个任务的完工期影响不大时,由中心极限定理可知,总完工期服从以TZ为均值,以Σσ2为方差的正态分布。
为达到严格控制工期,确保任务在计划期内完成的目的,我们可以计算在某一给定期限Ts前完工的概率。可以指定多个完工期Ts,直到求得有足够可靠性保证的计划完工期Ts*,将其作为总工期。完工概率求解公式如下:
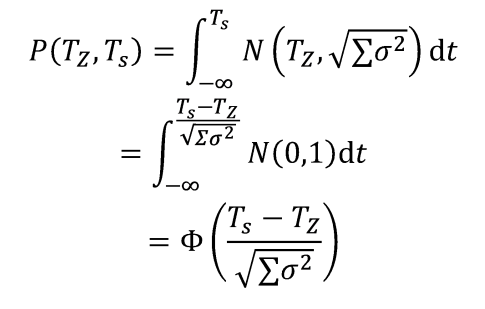
其中,N(TZ,(Σσ2)^1/2)是以TZ为均值,以(Σσ2)^1/2为均方差的正态分布。
概率型网络图时间参数的计算过程可以总结为以下几个步骤:
1、利用a,m,b求出各项工作的平均工时t和σ;
2、利用确定型网络图的方法,按照t值计算出各工作的最早开工时间、最迟开工时间和时差,确定关键路线和总完工期(期望工期);
3、求出完工概率。
与确定型工作时间不同的是,概率型计算出每一事项按期完工概率后,具有较小概率的事项应特别注意,凡是以它为完工时间工作均应加快工作进度。另外,还应注意那些从始点到终点完工日期与总工期相近的次关键路线,计算它们按总工期完工的概率,实施计划时要对其中完工概率较小的一些路线从严控制进度。
网络计划的优化
衡量一个计划的优劣,本应从工期、成本、资源消耗等方面综合评价,但是目前还没有一个能全面反映这些指标的综合数学模型,一般只是按照某一个或两个指标来衡量计划的优劣,不问的优化目标有不问的优化方法,接下来小编将举例说介绍几种优化的方法:
改变串联工作
让我们首先学习第一种网络计划优化的方法,把串联工作改为平行工作或交叉工作。
方法论
01
为了缩短整个任务的完工期,达到时间优化的目标,可以研究关键路线上串联的每一项工作有无可能改为平行工作或交叉进行的工作,以缩短工期。
例题展示
02
例题1:
如下图所示,原计划市场调研需12天(图a),如增加人力改为三组同时进行,则只需4天即可(图b)。
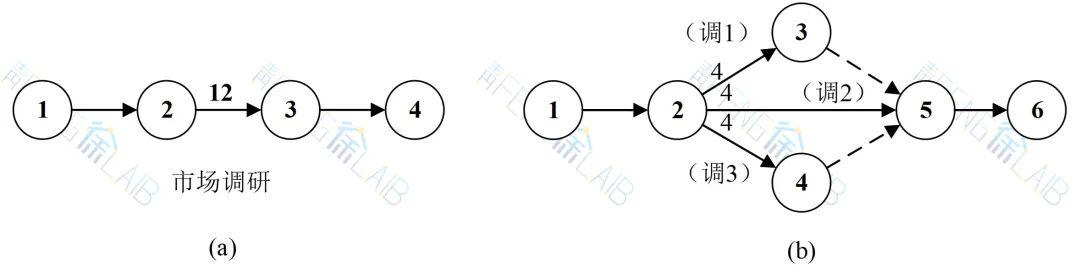
例题2:
又如下图所示之例,挖沟工作A需9天,埋管子工作B需6天,串联工作需时15天,而变为三段交叉工作,只需11天。这种方法虽然简单,但是行之有效。

利用时差
第二种优化方法是利用时差来优化工作时长。由于网络图中的非关键路工作都有时差,所以这些工作在开工时间上,具体工时上都具有一定的弹性。为了缩短任务的总工期,可以考虑放慢非关键工作的进度,减少这些工作的人力、资源,转去支援关键工作,以使关键工作的工时缩短来达到目的。
有限资源的合理分配
第三种优化方法为通过有限资源的合理分配来调整工期,使得工期最短。
方法论
01
一项任务的可用资源,一般情况下总是有限的,因此时间计划必须考虑资源问题,考虑如何在有限资源情况下使工期最短。
调整的基本原则是:
(1)尽量保证关键工作的日资源需求量。
(2)利用非关键工作的时差错开各工作的使用资源时间。
(3)在技术章程允许条件下,可适当延长时差大的工作的工时,或切断某些非关键工作,以减少日总需求量。
具体方法是按资源的日需求量所划分的时间段逐步从始点向终点进行调整。
例题展示
02
以人力资源为例,下图所示的网络图,已计算出关键路线为:①→②→③→⑤→⑥,总工期为11天。箭杆上△中标注数字为工作每天所需人力数(假设所有工作都需要同一种专业工人)。

画出带日程的网络图及资源动态曲线,如下图(图中虚线为非关键工作的总时差)。

由图可见,若按每道工作的最早开工时间安排,人力需求很不均匀,最多者为20人/日,最少为1人/日,这种安排即使在人力资源充足条件下也是很不经济的。现假设资源有限,每日可用人力为10人。下面进行计划调整,希望能不延迟总工期或尽量少延迟。
本例中,第一个时间段为[0,2],需求量为18人/日,在调整时要对本时间段内各工作按总时差的递增顺序排队编号,如:
工作(1,2),总时差0,编为1#
工作(1,4),总时差1,编为2#
工作(1,6),总时差7,编为3#
对编号小的优先满足资源需求量,当累计和超过10人时,未得到人力安排的工作应移入下一时间段,本例中工作(1,2)与(1,4)人力日需求量为9,而工作(1,6)需9人/日,所以应把(1,6)移出[0,2]间段后开工,见下图。

接着调整[2,3]间段。在编号时要注意,如果已进行的非关键工作不允许中断,则编号要优先考虑,把它们按照新的总时差与最早开始时间之和的递增顺序排列,否则同第一段的编号规则。
本例中(1,4)为已进行中工作,假设不允许中断。而(2,3)为关键工作,(1,6)还有时差5天,则编号顺序为:
工作(1,4),总时差1,编为1#
工作(2,3),总时差0,编为2#
工作(1,6),总时差5,编为3#
累加所需人力资源数,工作(1,4)与(2,3)共需10人/日,所以工作(1,6)要移出[2,3]时间段,调整结果见下图。

以后各时间段类似处理,经过几次调整,可得下图。此时人力日需求量已满足不超过10人的限制,总工期未受影响,必要时总工期可能会延迟。这种方法也可用于多种资源分配问题。
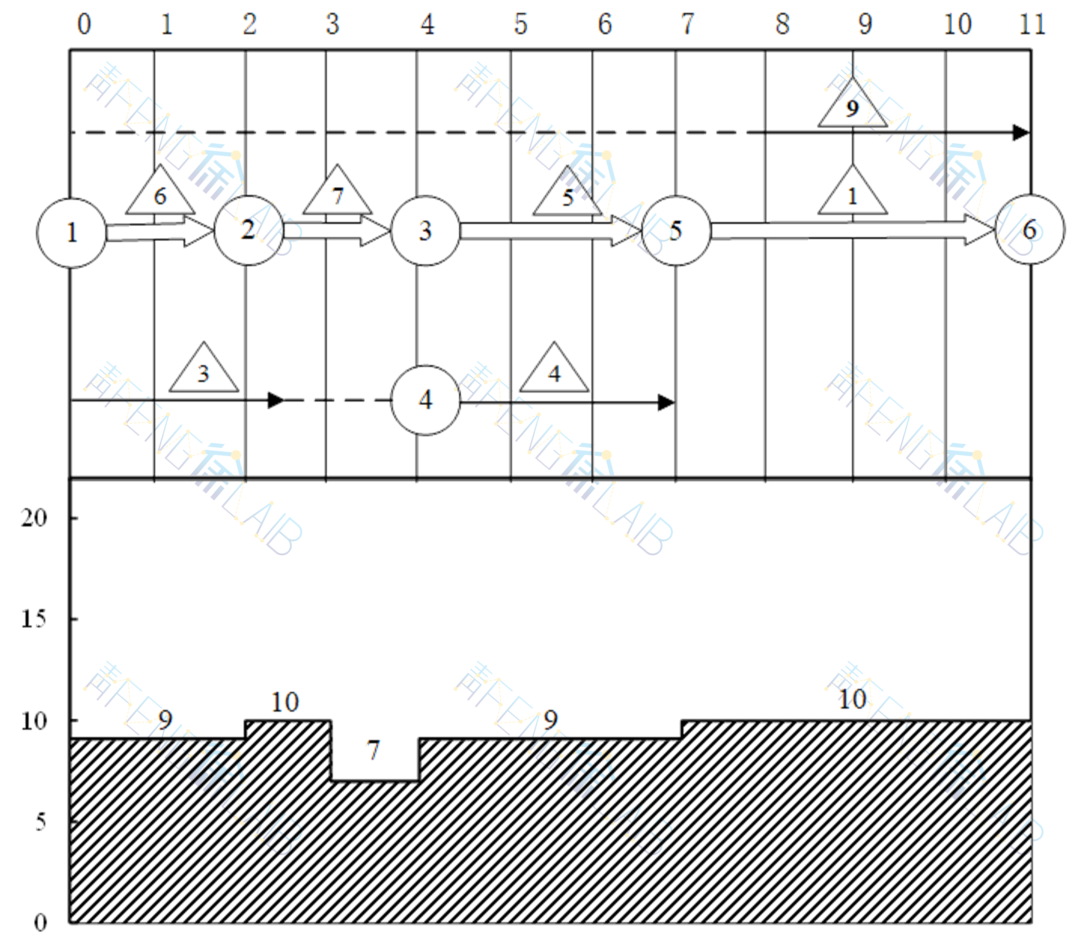
需要说明的是,由于编号及调整规则只是一种原则,所以调整结果常常是较好方案,不一定是工期最短方案。由于求精确解有时很繁难,网络优化中多采用这类近似算法。
最低成本日程
方法论
01
项目或任务的成本一般包括直接费用和间接费用两部分。
直接费用是完成各项工作直接所需人力、资源、设备等费用,为缩短工作的作业时间,需采用一些技术组织措施,相应会增加一些费用,在一定范围内,工作的作业时间越短,直接费用越大。
间接费用则包括管理费、办公费等,常按任务期长短分摊,在一定条件下,工期越长,间接费用越大。它们与工期的关系如下图所示。
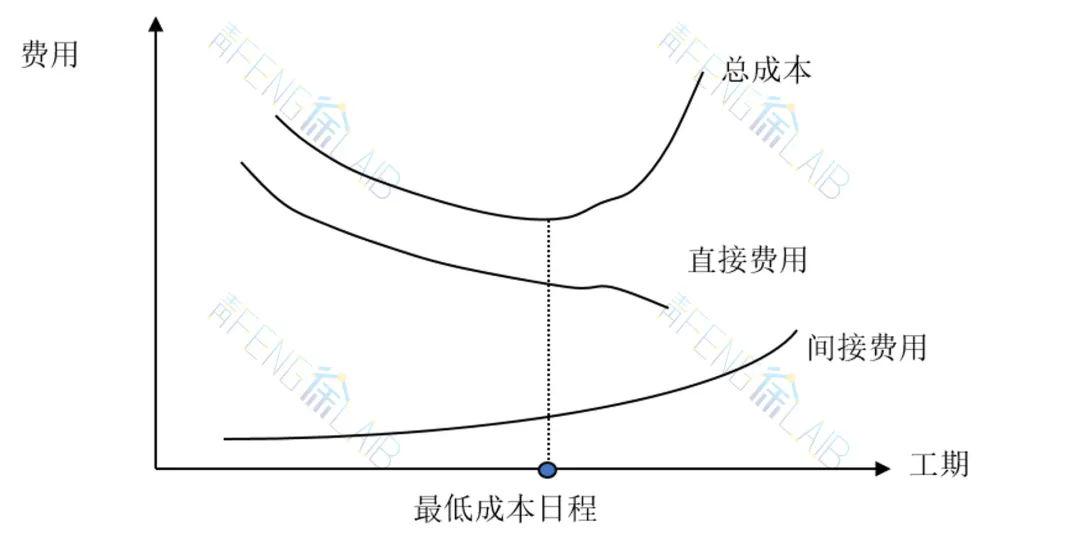
工期缩短时直接费用要增加而间接费用减少,总成本是由直接费用与间接费用相加而得。通过计算网络计划的不同完工期相应的总费用,以求得成本最低的日程安排就是“最低成本日程”,又称“工期一成本”优化。
直接费用与工作所需工时关系,常假定为直线关系,如下图所示。工作(i,j)的正常工时为Dij,所需费用Mij,特急工时为dij,所需费用mij,工作(i,j)从正常工时每缩短一个单位时间所需增加的费用称为成本斜率,用cij表示。

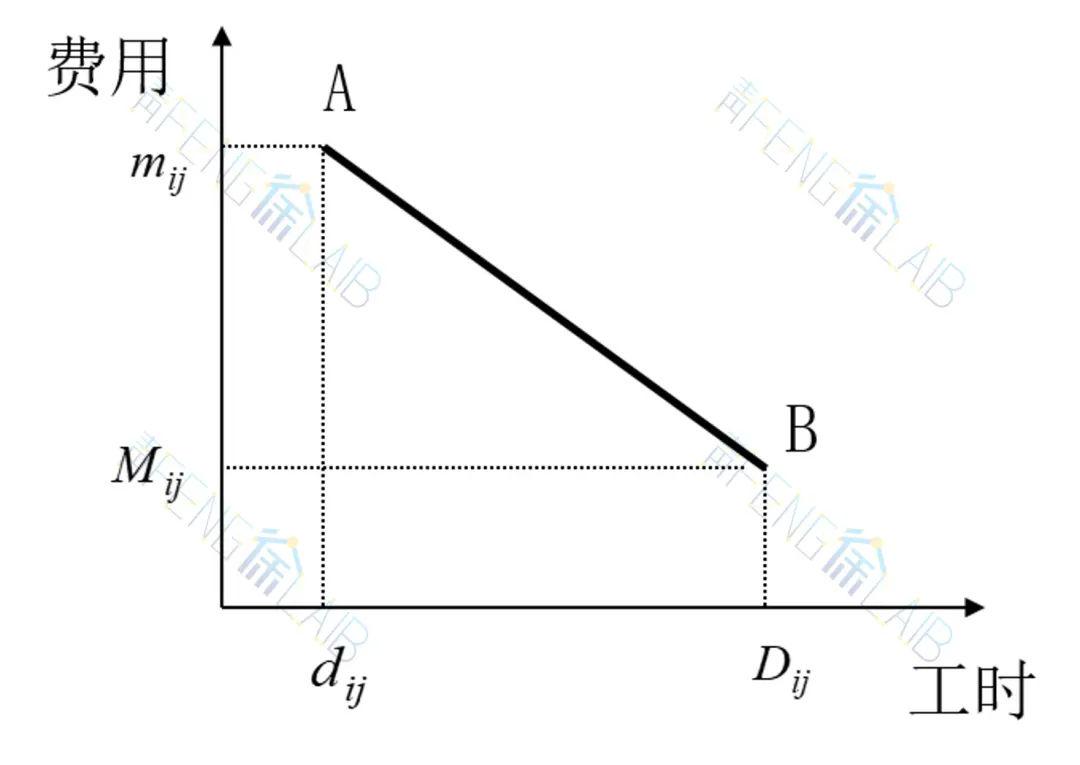
如某工作正常工时为5天,费用600元;按特急工时3天进行所需费用为900元,则

(元/天),即每缩短一天需增加费用150元。接下来我们通过一个简例说明最低成本日程的计算方法。
例题展示
02
已知网络计划各工作的正常工时、特急工时及相应直接费用如下表,网络图如下图所示。

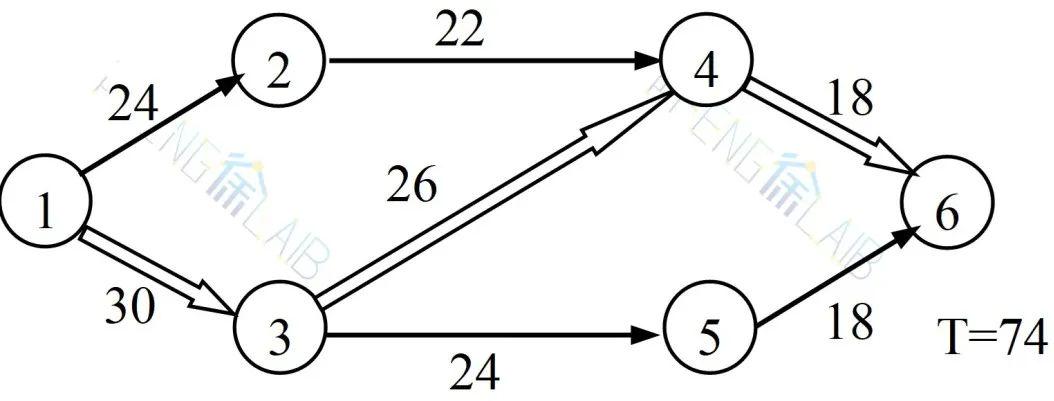
按正常工时从图中计算出总工期为74天。关键路线为①→③→④→⑥,由上表可计算出正常工时情况下总直接费用为47800元。
设正常工时下,任务总间接费用为18000元,工期每缩短一天,间接费用可节省330元,求最低成本日程。
解:以上图所示的原始网络为基础,计算按下列步骤进行:
(1)从关键工作中选出缩短工时所需直接费用最少的方案,并确定该方案可能缩短的天数。
(2)按照工作的新工时,重新计算网络计划的关键路线及关键工作。
(3)计算由于缩短工时所增加的直接费用。
不断重复上述三个步骤,直到工期不能再缩短为止。
第一次调整
从上图看出,关键路线上的三道关键工作(1,3),(3,4),(4,6)中,工作(1,3)的成本斜率最小(100),应选择在工作(1,3)上缩短工时,查上表知,最多可缩短12天,即取工作(1,3)新工时为30-12=18(天)。重新计算网络图时间参数结果如下图(a)所示,关键路线为①→②→④→⑥,工期为64天,实际只缩短了10天。这意味着(1,3)工作没有必要减少12天,(1,3)工时应取30-10=20(天)。重新计算,结果如下图(b),总工期为64天,有两条关键路线:①→②→④→⑥与①→③→④→⑥,此次调整增加直接费用10×100=1000(元)。

第二次调整
重复步骤(1),(2),(3),必须注意两条关键路线应同时缩短。有如下几个方案可选择:
(1)在(1,3)与(1,2)上同时缩短一天,需费用100+250=350(元);
(2)在(1,3)与(1,2)上同时缩短一天,需费用100+200=300(元);
(3)在(3,4)与(1,2)上同时缩短一天,需费用150+250=400(元);
(4)在(3,4)与(2,4)上同时缩短一天,需费用150+200=350(元);
取费用最小方案为方案(2),(1,3)最多可缩短2天,(2,4)可缩短4天,取其中小者,即将(1,3)与(2,4)的工时分别改为20-2=18(天),22-2=20(天)。
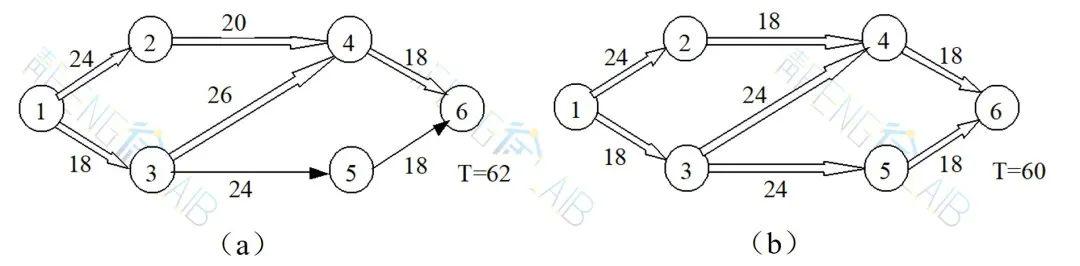
重新计算网络图时间参数,结果见下图(a)。总工期为62天,这时关键路线仍为2条:①→②→④→⑥与①→③→④→⑥,增加直接费用2×300=600(元)。
第三次调整
选择费用最小的方案,在工作(2,4)与(3,4)上各缩短2天,即(2,4)与(3,4)的工时分别改为20-2=18(天),26-2=24(天),重新计算网络图时间参数,结果见下图(b)。总工期为60天,关键路线为:①→②→④→⑥,①→③→④→⑥和①→③→⑤→⑥,所增加的直接费用为2× 350=700(元)。
由于一条关键路线①→③→④→⑥上各工作工时已不能缩短,计算结束。
全部计算过程及相应费用变化列成下表。由表中可见,最低成本日程为62天,总成本为63440元。
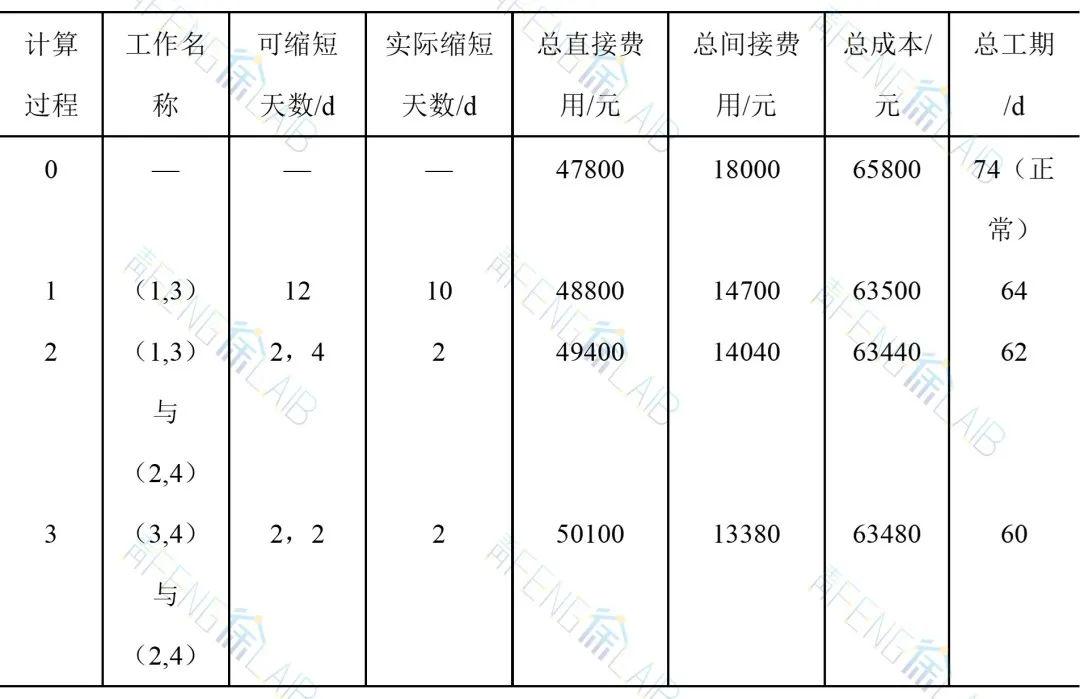
关于最低成本日程的计算步骤,也可改为计算总费用,并与上一次的总费用进行比较,若费用不能再降低则停止计算。
实施计划的管理
网络计划技术是先进的科学方法,但毕竟只是计划,在制订时就包含着许多不确定的因素,所以在计划的实施阶段还必须不断检查,进行分析,及时地采取措施修订计划,才能确保计划的实现。
实施计划的监督与管理的主要内容为:
(1)执行情况的报告。指计划执行单位应定期向主管部门报告计划执行进展情况,包括各工作原计划工时、预定完工期、时差、当前进展情况等。
(2)计划主管部门对报告进行加工分析。主管部门(或计算中心)的调度小组应根据收到的报告资料核对原网络计划作出必要修改。主要修改内容为:将已完成的工作或因某些原因需要取消的工作从网络图中消去;根据实施情况,修改某些未完成工作所需工时或添加某些新的工作。修改后要按新网络图,重新计算有关的时间参数和关键路线、总工期。
(3)网络计划的调整。如果计算出的新工期不符合预定工期就需要进行调整。通过对计划、实际资源、人力的研究,对网络计划的逻辑顺序、工作工时进行修订,使调整后的计划符合预定工期。此外还应进行财务控制,即检查工作是否在预定费用内进行。
完整的网络计划技术是一个管理系统,即最优的计划、精确的情报信息,再加上系统管理,才是网络计划技术的全部精髓。