电子技术——反馈系统概述

许多物理系统都会形成反馈系统。但是有趣的是，负反馈系统理论却是由电子工程师所完善的。自从1928年第一个负反馈放大器诞生开始，负反馈系统从此登上历史的舞台，现在负反馈系统不光只用在电子工程上，而且还渗透到各个学科上，例如生物学。

反馈系统可以分为 负反馈 和 正反馈 。在放大器设计中，使用负反馈的主要原因是：

1. 稳定增益：让放大器的增益尽量稳定，减少对外界因素的依赖，例如温度。
2. 减少非线性失真：让放大器的输出正比于输入。
3. 减少噪声影响：减少输出中无关信号的产生。
4. 控制输入和输出阻抗：通过选择不同的反馈网络的拓扑结构，增加或减少输入和输出阻抗。
5. 扩大放大器带宽。

反馈网络实现上述所有特性的代价就是减小了增益系数。减小的倍数我们称为 反馈因子 ，实际上反馈因子还出现在其他特性上，例如带宽增大了反馈因子倍。总之，负反馈的核心思想就是在各种特性中进行折中。本章我们学习反馈系统的分析、设计和特性。

在一些特定的条件下，负反馈放大器可能变成正反馈以及引起不必要的震荡。实际上，我们将会在之后的章节学习正反馈实现的震荡电路和双稳态电路。在本章，我们只关心稳态放大器，我们将会学习放大器的问题问题以及如何抑制不必要的震荡。

信号流程图

下图展示了一个基本的负反馈放大器：

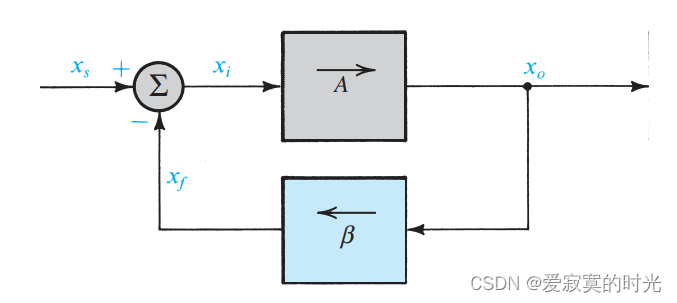
为了一般化表示，我们不使用电流量或者电压量这种具体的物理量表示，而是使用代数 量$x$ 表示。该放大器是单边的，增益为 $A$ ，称为 开环增益 ，输出为：

$$x_o=A{x}_i$$

图片下面的 反馈网络 对输出量进行测量或采样，提供一个负反馈信号 $x_f$ ：

$$x_f=\beta x_o$$

这里的 $\beta$ 称为 反馈因子 。

现在我们假设连接到输出端的反馈网络不会改变放大器的增益或是 $x_o$ 。也就是反馈网络不会重写放大器的输出。并且，放大器是单边的。

负反馈信号从源信号 $x_s$ 中减去得到输入信号：

$$x_i=x_s-x_f$$

这里我们注意到减法操作使得反馈是负反馈，负反馈减小了输入量的强度。这里我们建设，负反馈信号和源信号通过减法器或是差分输入到放大器中，即反馈网络不会重写放大器的输入。

闭环增益

负反馈放大器的增益，称为 闭环增益 或是负反馈增益，记为 $A_f$ ，定义为：

$$A_f\equiv \frac{x_o}{x_s}$$

带入上面的表达式我们得到：

$$A_f=\frac{A}{1+A\beta }$$

我们称 $A\beta$ 为 环路增益 ，若反馈是负反馈，则 $A\beta$ 一定是一个正数，也就是说，$x_s$ 必须和 $x_f$ 同号，这样才能产生一个更小的 $x_i$ 。上式表示，闭环增益是开环增益的 $\frac{1}{1+A\beta }$ 倍，我们称 $\frac{1}{1+A\beta }$ 为 反馈量 。

对于一些电路， $A\beta \gg 1$ 此时闭环增益可以近似为：

$$A_f\simeq \frac{1}{\beta }$$

这是一个有意思的结果，这表明若环路增益较大，那么闭环增益几乎完全取决于负反馈网络。因为反馈网络通常使用被动元件组成，因此可以选用数值更加精确的被动元件，从而获得更加准确、稳定的闭环增益，这也是负反馈放大器的优点之一。换句话说，闭环增益对 $A$ 的依赖性非常小，这也是我们所期望的，因为 $A$ 是由放大器的设计师或是生产厂商所决定的，具有较大的波动范围。我们已经在运算放大器的章节中体会到了这一点，其中运算放大器的闭环增益完全取决于负反馈网络。一般情况下，我们将 $1/\beta$ 视为 $A_f$ 。

同时，我们还能导出 $x_f$ 和 $x_s$ 的关系：

$$x_f=\frac{A\beta }{1+A\beta }{x}_s$$

因为 $A\beta \gg 1$ 所以 $x_f\simeq x_s$ 这说明输入信号 $x_i$ 降低至几乎为零。此时 $x_i$ 被称为 误差信号 。对应的，输入端的差分输入电路被称为 比较电路 。

同时，我们还能导出 $x_i$ 和 $x_s$ 的关系：

$$x_i=\frac{1}{1+A\beta }{x}_s$$

当 $A\beta$ 非常大的时候，此时 $x_i$ 非常小，这也是运算放大器在输入端的特性，观察到负反馈网络将输入的信号强度减小了 $\frac{1}{1+A\beta }$ 倍。在之后我们会发现，这增加了放大器的线性特性。

环路增益

从上述分析中，我们知道环路增益 $A\beta$ 是一个非常重要的量，实际上是负反馈放大器中最重要的参数：

1. 环路增益 $A\beta$ 符号决定了反馈的类型。在负反馈放大器中 $A\beta$ 必须是一个正数。
2. 环路增益 $A\beta$ 的大小决定了 $A_f$ 与理想值 $\frac{1}{\beta }$ 之间的误差。
3. 环路增益 $A\beta$ 的大小决定了反馈量 $1+A\beta$ ，反馈量决定了负反馈放大器的各个特性的值。
4. 在以后我们会知道，在一些特定的频率下， $A\beta$ 可能会变成负值，这会使得放大器不稳定。设计一个稳定的放大器需要修改放大器的频率特性使得 $A\beta$ 正常工作。

为了确定环路增益，我们可以使用下面的方法：

1. 让 $x_s=0$ 。
2. 断开反馈网络和输出端的连接。因为反馈网络不重写输出，因此我们可以让增益 $A$ 保持不变。
3. 在反馈网络的输入端输入一个测试信号 $x_t$ 并测量放大器的输出信号 $x_r$ 。

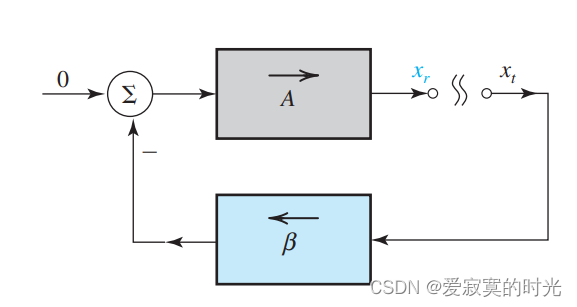
我们可以得出：

$$x_r=-A\beta x_t$$

则环路增益为：

$$A\beta =-\frac{x_r}{x_t}$$

我们注意到，若 $A\beta$ 是正的，那么 $x_r$ 和 $x_t$ 必须是反相信号。这个方法也被用来测试反馈放大器的极性。

总结