1.什么是Adaboost

        AdaBoost（adapt boost），自适应推进算法，属于Boosting方法的学习机制。是一种通过改变训练样本权重来学习多个弱分类器并进行线性结合的过程。它的自适应在于：被前一个基本分类器误分类的样本的权值会增大，而正确分类的样本的权值会减小，并再次用来训练下一个基本分类器。同时，在每一轮迭代中，加入一个新的弱分类器，直到达到某个预定的足够小的错误率或预先指定的最大迭代次数再确定最后的强分类器。Adaboost主要解决的问题有: 两类问题、多类单标签问题、多类多标签问题、回归问题。

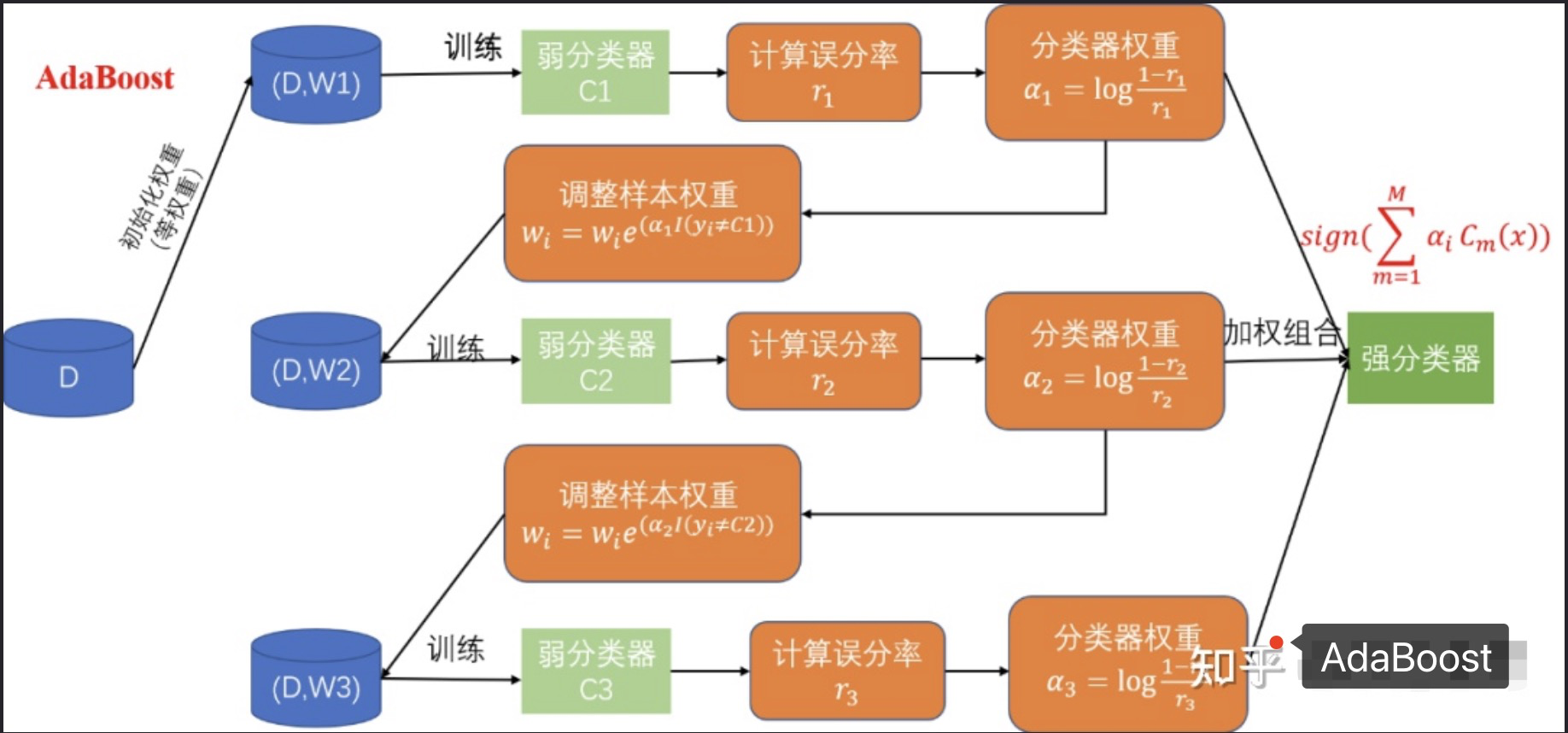
2.Adaboost算法流程

2-1 权值初始化

        初始化训练数据的权值分布D1。假设有N个训练样本数据，则每一个训练样本最开始时，都会被赋予相同的权值：w1 = 1/N。

2-2 训练弱分类器

         训练弱分类器Ci。训练过程中提高被弱分类器错分样本的权值，降低正分样本的权值，作为下一轮基本分类器的训练样本。这样一来，那些没有得到正确分类的数据，由于其价值加大后收到后一轮弱分类器的更大关注，于是，分类问题被一系列弱分类器"分而治之"。具体训练过程：如果某个训练样本点，被弱分类器Ci准确地分类，那么再构造下一个训练集中，它对应的权值要减小；相反，如果某个训练样本点被错误分类，那么它的权值就应该增大。权值的更新过的样本被用于训练下一个弱分类器，整个过程如此迭代下去。​​​​​​​​​​​​​​

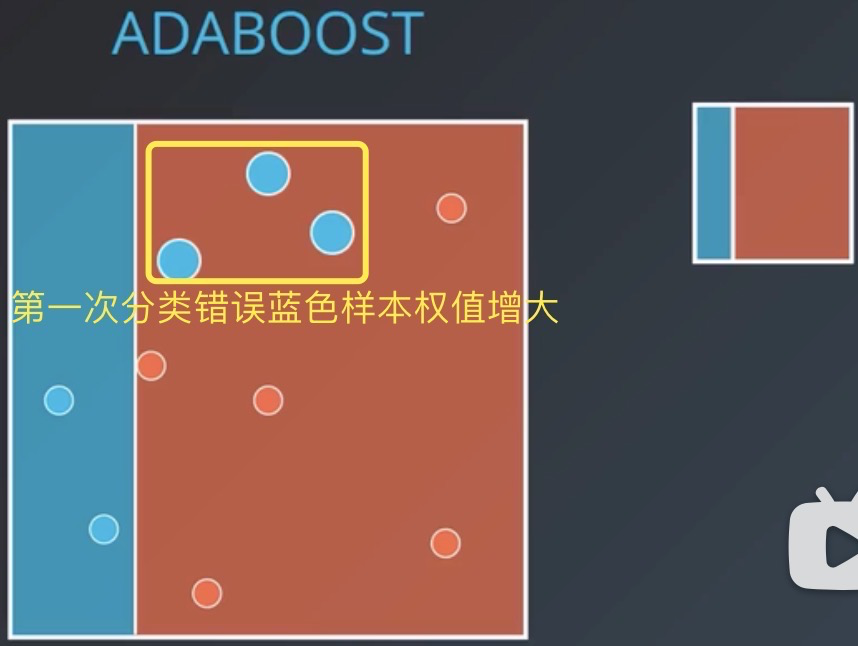
        第一个分类器将三个蓝色样本错误分类到红色样本区域，所以将蓝色样本的权值增大，作为第二个分类器的训练数据。

         第二个分类器将两个蓝色样本错误分类到红色样本区域同时也将一个红色样本错误分类到蓝色样本区域，所以对应的蓝色样本和红色样本的权值增大，作为第三个分类器的训练数据。 

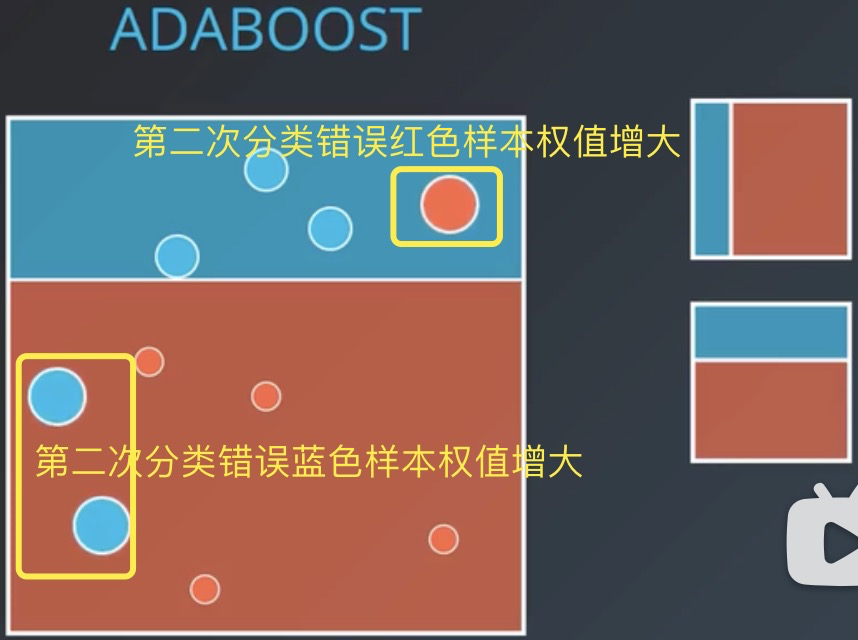
        第三个分类器将经过前两个分类器后进行权值调整的数据再次训练，并进行划分。

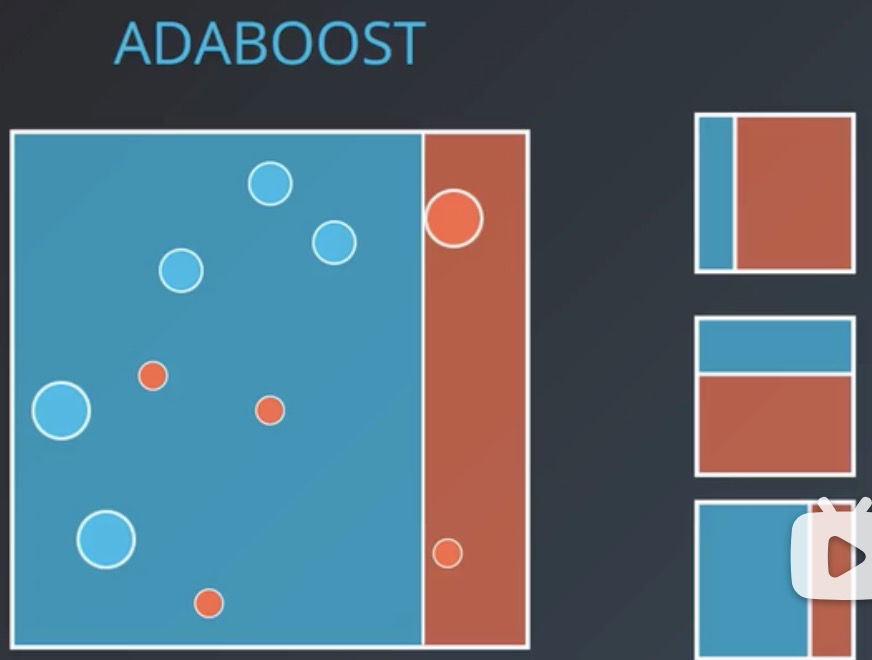
2-3 集成组合        

        将各个训练得到的弱分类器组合成一个强分类器。采取加权多数表决的方法，误差率小的分类器的权值大，使其在表决过程中起较大作用。        

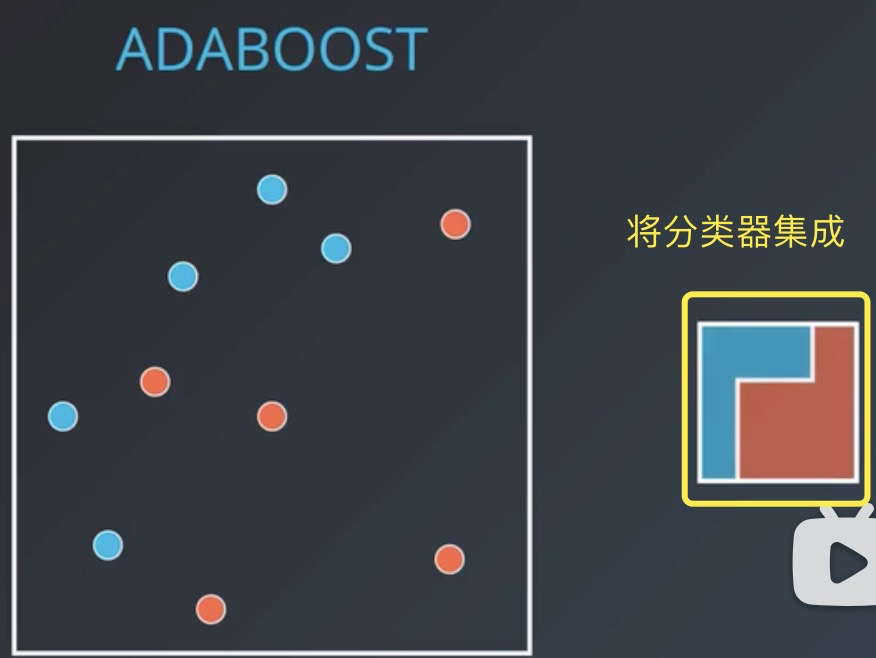
        各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。误差率低的弱分类器在最终分类器中占的权重较大，误差率高的弱分类器在最终分类器中占的权重较小。 

3.Adaboost公式推导

3-1 Adaboost 公式

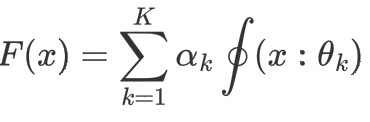
3-1 推导 

4.Adaboost的优点和缺点

4-1 优点

（1）Adaboost提供一种框架，在框架内可以使用各种方法构建子分类器。可以使用简单的弱分类器，不用对特征进行筛选，也不存在过拟合的现象。

（2）Adaboost算法不需要弱分类器的先验知识，最后得到的强分类器的分类精度依赖于所有弱分类器。无论是应用于人造数据还是真实数据，Adaboost都能显著的提高学习精度。

（3）Adaboost算法不需要预先知道弱分类器的错误率上限，且最后得到的强分类器的分类精度依赖于所有弱分类器的分类精度，可以深挖分类器的能力。Adaboost可以根据弱分类器的反馈，自适应地调整假定的错误率，执行的效率高。

（4）Adaboost对同一个训练样本集训练不同的弱分类器，按照一定的方法把这些弱分类器集合起来，构造一个分类能力很强的强分类器，即“三个臭皮匠赛过一个诸葛亮”。

4-2 缺点

        在Adaboost训练过程中，Adaboost会使得难于分类样本的权值呈指数增长，训练将会过于偏向这类困难的样本，导致Adaboost算法易受噪声干扰。此外，Adaboost依赖于弱分类器，而弱分类器的训练时间往往很长。