1.N 叉树的最大深度

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例 1：

 

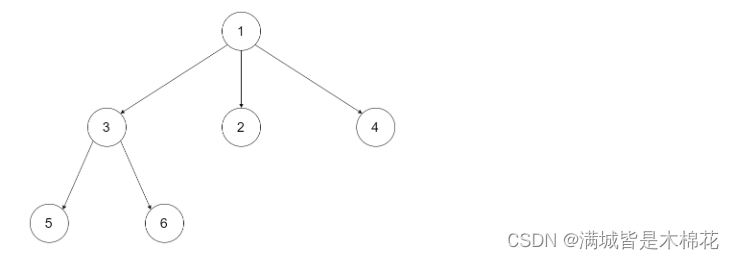
输入：root = [1,null,3,2,4,null,5,6]
输出：3

 解题思路:

使用递归法求解：

/**
 * // Definition for a Node.
 * function Node(val,children) {
 *    this.val = val;
 *    this.children = children;
 * };
 */
/**
 * @param {Node} root
 * @return {number}
 */
var maxDepth = function(root) {
  if(!root) return 0                // 如果没有节点, 直接返回0
  let num = 0                       // 记录深度
  if(root.children){
    root.children.forEach(item=>{   // 遍历有几个节点
      let max = maxDepth(item)      // 递归调用
      num = Math.max(max, num)      // 对比当前和之前得到的 深度, 保留大的
    })
  }
  return num + 1                    // 顶级节点算一个 得加1
};

2.二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。 

解题思路也是同样使用递归算法：

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    if(!root){
        return 0;
    }
    return 1+Math.max(maxDepth(root.left),maxDepth(root.right));
};

3.二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]

输出：2

 解题思路：

根节点为空返回null 递归遍历左子树和右子树，返回左子树和右子树中节点深度的最小值 如果左或右子树中有一树为空直接返回左+右子树的节点+1 代码

var minDepth = function(root) {
  //根节点为空返回空
  if(!root) return null;
  //查看一下左子树的深度
  let left=minDepth(root.left);
  //查看一下右子树的深度
  let right=minDepth(root.right);
  //如果左子树或右子树有一层为空就返回当前左（或右）子树的值加1，加零相当于没加
  if(!left || !right) return left+right+1;
  //最后返回一个左右子树的最小值加1
  return Math.min(left,right)+1;
};