🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
目录
第五章 相似矩阵及二次型
&4)对称阵的对角化
&5二次型及其标准型
&6)用配方法化二次型成标准型
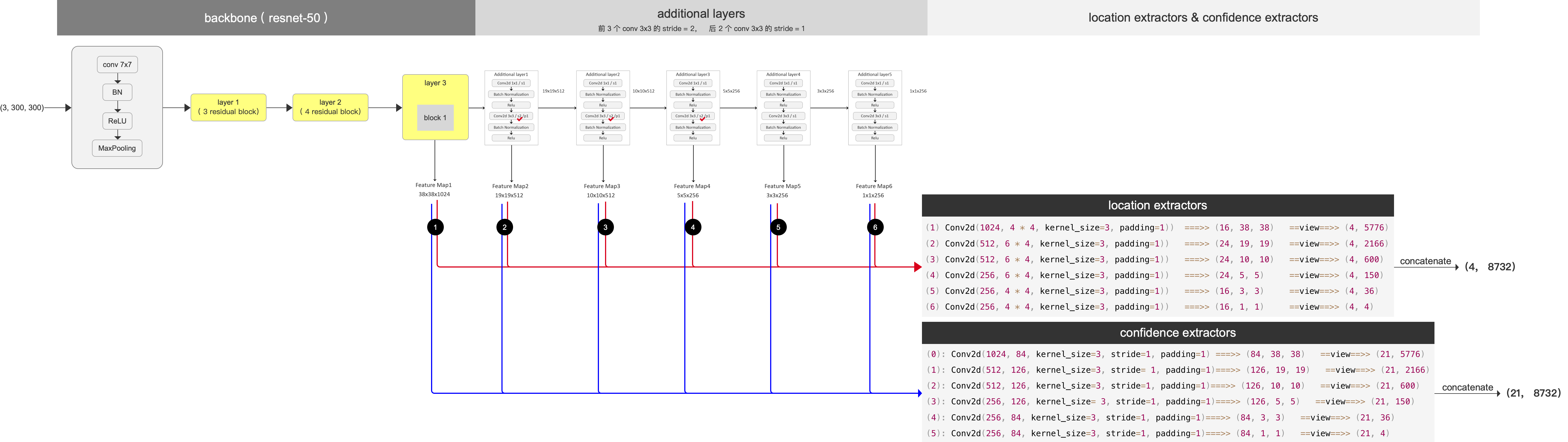
第五章 相似矩阵及二次型
&4)对称阵的对角化
性质1 对称阵的特征值为实数
性质2 设𝛌[1],𝛌[2],是对称矩阵A的两个特征值,p[1],p[2]是对应的特征向量,若𝛌[1]!=𝛌[2],则p[1]与p[2]正交
定理5 设A为n阶对称矩阵,则必有正交矩阵P,使P^-1AP=P^TAP=⩘,其中⩘是以A的n个特征值为对角元的对角矩阵
推论 设A为n阶对称矩阵,𝛌是A的特征方程的k重根,则矩阵A-𝛌E的秩R(A-𝛌E)=n-k,从而对应特征值𝛌恰有k个线性无关的特征向量
对称矩阵:A=A^T
&5二次型及其标准型
定义8: 含有n个变量x[1],x[2],…,x[n]的二次齐次函数
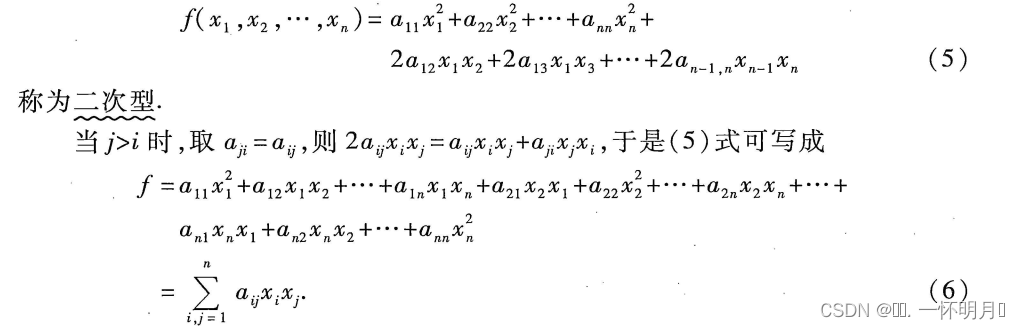
对于二次型,我们讨论的主要问题是:寻求可逆的线性变换

&6)用配方法化二次型成标准型
吃技巧(没有固定章法)
🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸








![W806(一)模拟IIC驱动0.96OLED[移植]](https://img-blog.csdnimg.cn/img_convert/ec383412f5424165b2a66c1c268cd1ad.jpeg)