目录

一。拉普拉斯矩阵的定义

二。谱聚类算法：未正则拉普拉斯矩阵 

三。谱聚类算法：随机游走拉普拉斯矩阵

四。谱聚类算法：对称拉普拉斯矩阵

五。进一步思考

 六。随机游走和拉普拉斯矩阵的关系

 七。标签传递算法

---

一。拉普拉斯矩阵的定义

计算点之间的邻接相似度矩阵W

        若两个点的相似度值越大，表示这两个点越相似；
        同时，定义wij=0表示vi,vj两个点没有任何相似性(无穷远) 

W的第i行元素的和为vi的度。形成顶点度对角阵D

        dii表示第i个点的度
        除主对角线元素，D其他位臵为0

未正则的拉普拉斯矩阵：L=D-W

正则拉普拉斯矩阵

二。谱聚类算法：未正则拉普拉斯矩阵 

输入：n个点{pi}，簇的数目k

        计算n×n的相似度矩阵W和度矩阵D；
        计算拉普拉斯矩阵L=D-W；
        计算L的前k个特征向量u1,u2,...,uk；
        将k个列向量u1,u2,...,uk组成矩阵U，U∈Rn×k；
        对于i=1,2,...,n,令yi∈Rk是U的第i行的向量；
        使用k-means算法将点(yi)i=1,2,...,n聚类成簇C1,C2,...Ck；
        输出簇A1,A2,...Ak，其中，Ai={j|yj∈Ci}

三。谱聚类算法：随机游走拉普拉斯矩阵

输入：n个点{pi}，簇的数目k

        计算n×n的相似度矩阵W和度矩阵D；
        计算正则拉普拉斯矩阵Lrw=D-1(D-W)；
        计算Lrw的前k个特征向量u1,u2,...,uk；
        将k个列向量u1,u2,...,uk组成矩阵U，U∈ Rn×k ；
        对于i=1,2,...,n,令yi∈Rk是U的第i行的向量；
        使用k-means算法将点(yi)i=1,2,...,n聚类成簇C1,C2,...Ck ；
        输出簇A1,A2,...Ak，其中，Ai={j|yj∈Ci}

四。谱聚类算法：对称拉普拉斯矩阵

输入：n个点{pi}，簇的数目k
        计算n×n的相似度矩阵W和度矩阵D；
        计算正则拉普拉斯矩阵Lsym=D-1/2(D-W) D-1/2；
        计算Lsym的前k个特征向量u1,u2,...,uk；
        将k个列向量u1,u2,...,uk组成矩阵U，U∈Rn×k；
        对于i=1,2,...,n,令yi∈Rk是U的第i行的向量；
        对于i=1,2,...,n,将yi∈Rk依次单位化，使得|yi|=1；
        使用k-means算法将点(yi)i=1,2,...,n聚类成簇C1,C2,...Ck；
        输出簇A1,A2,...Ak，其中，Ai={j|yj∈Ci}

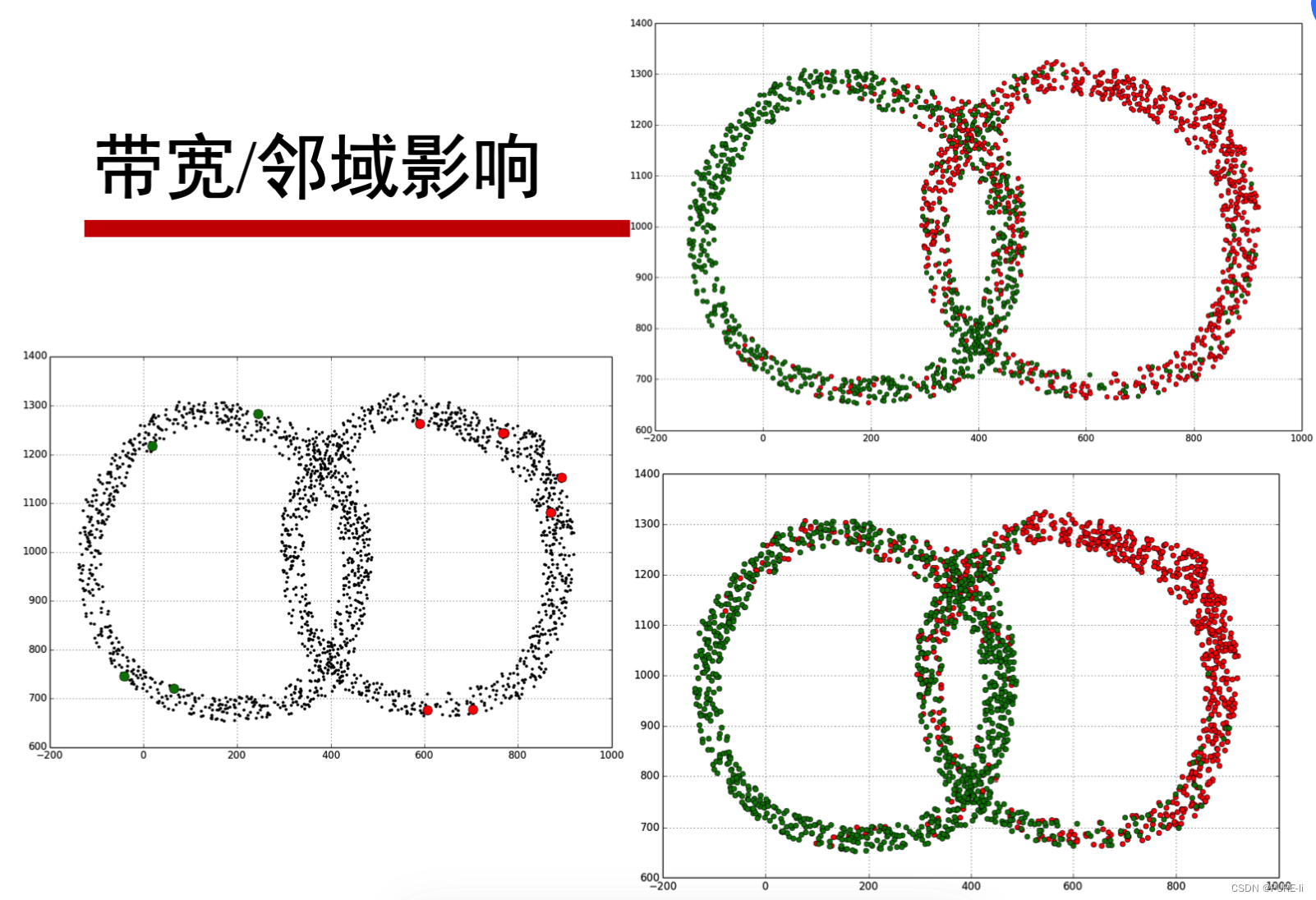
五。进一步思考

 六。随机游走和拉普拉斯矩阵的关系

图论中的随机游走是一个随机过程，它从一个顶点跳转到另外一个顶点。谱聚类即找到图的一个划分，使得随机游走在相同的簇中停留而几乎不会游走到其他簇。

 七。标签传递算法

对于部分样本的标记给定，而大多数样本的标记未知的情形，是半监督学习问题。

标签传递算法(Label Propagation Algorithm,LPA)，将标记样本的标记通过一定的概率传递给未标记样本，直到最终收敛。