两类AC的改进算法

整理了动手学强化学习的学习内容

1. TRPO 算法（Trust Region Policy Optimization）

1.1. 前沿

策略梯度算法即沿着梯度方向迭代更新策略参数 。但是这种算法有一个明显的缺点：当策略网络沿着策略梯度更新参数，可能由于步长太长，策略突然显著变差，进而影响训练效果。

针对以上问题，考虑在更新时找到一块信任区域（trust region），在这个区域上更新策略时能够得到某种策略性能的安全性保证，这就是信任区域策略优化（trust region policy optimization，TRPO）算法的主要思想。

1.2. 一些推导

首先，最常规的动作价值函数，状态价值函数，优势函数定义如下：
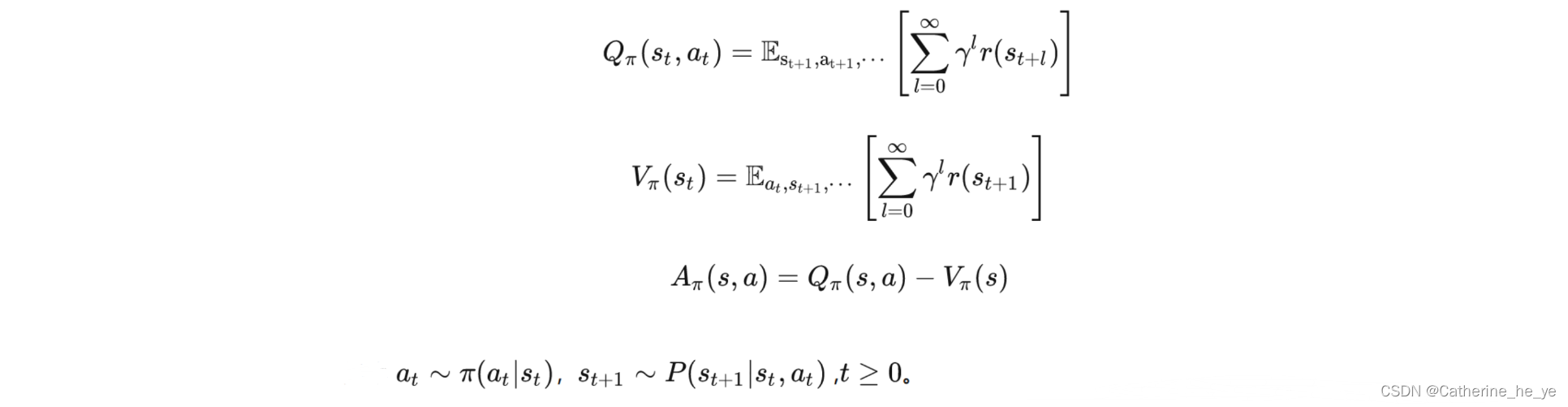接着，一个策略的好坏可以期望折扣奖励$J({\pi }_{\theta })$表示：
$$J({\pi }_{\theta })=E_{s_0,a_0,...}[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t)]=E_{s_0}[V^{{\pi }_{\theta }}(s_0)]$$

其中，$s_0\sim {\rho }_0(s_0)$，$a_t\sim {\pi }_{\theta }(a_t|s_t)$，$a_{t+1}\sim P(s_{t+1}|s_t,a_t)$。
由于初始状态$s_0$的分布${\rho }_0$和策略无关，因此上述策略${\pi }_{\theta }$下的优化目标$J({\pi }_{\theta })$可以写成在新策略${\pi }_{{\theta }^{\prime }}$的期望形式：
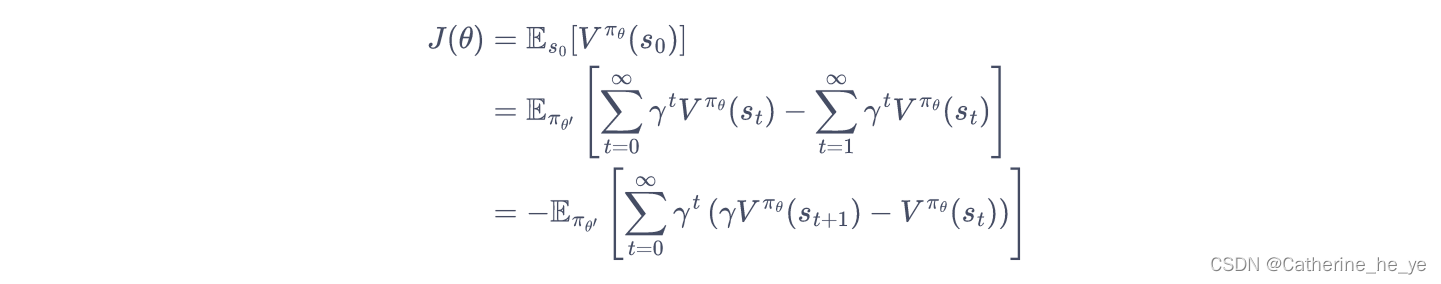从而，推导新旧策略的目标函数之间的差距：
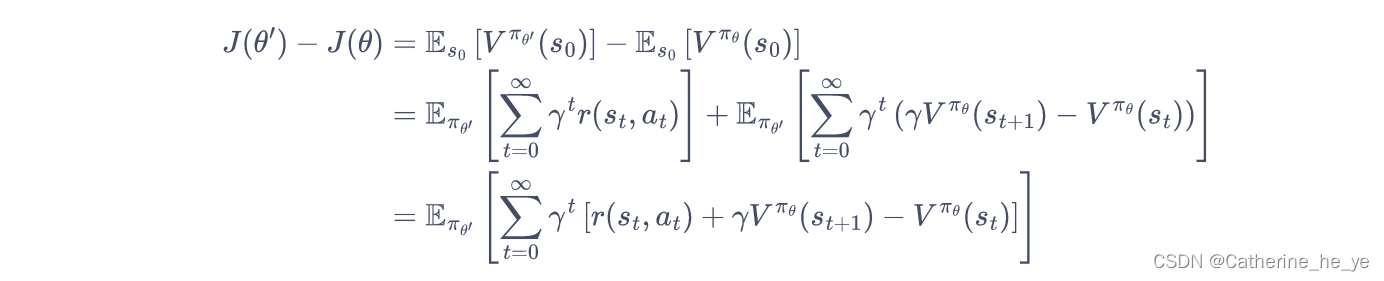将时序差分残差定义为优势函数A：
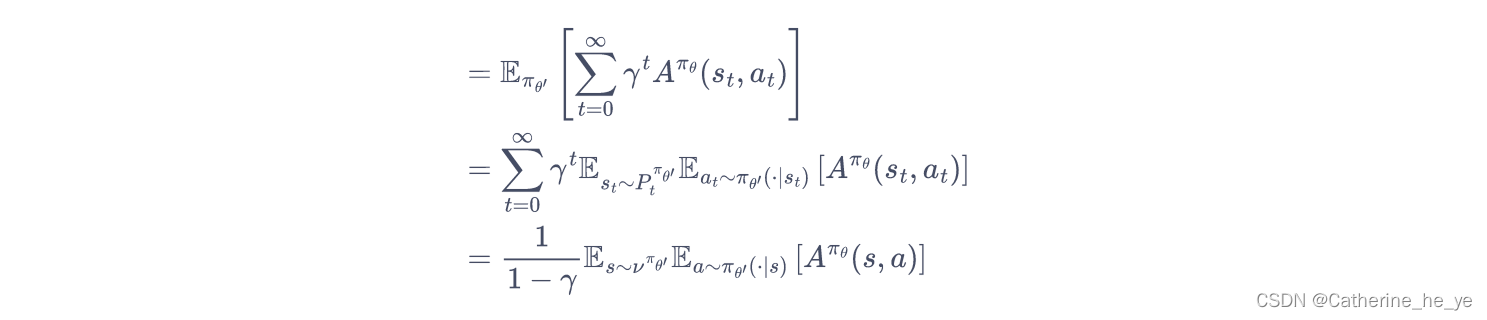所以只要我们能找到一个新策略，使得$J({\theta }^{\prime })-J(\theta )>=0$，就能保证策略性能单调递增。

但是直接求解该式是非常困难的，因为${\pi }_{{\theta }^{\prime }}$是我们需要求解的策略，但我们又要用它来收集样本。把所有可能的新策略都拿来收集数据，然后判断哪个策略满足上述条件的做法显然是不现实的。

于是 TRPO 做了一步近似操作，对状态访问分布进行了相应处理。具体而言，忽略两个策略之间的状态访问分布变化，直接采用旧的策略的状态分布，定义如下替代优化目标：
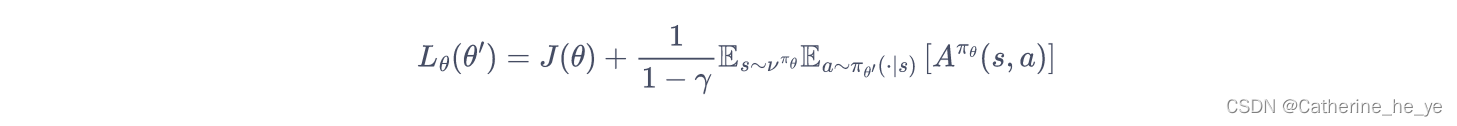当新旧策略非常接近时，状态访问分布变化很小，这么近似是合理的。其中，动作仍然用新策略${\pi }_{{\theta }^{\prime }}$采样得到，我们可以用重要性采样对动作分布进行处理：
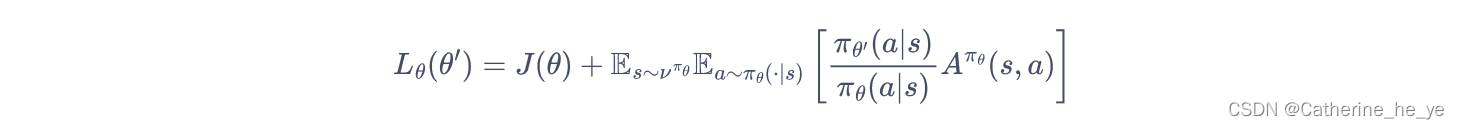为了保证新旧策略足够接近，TRPO 使用了KL散度来衡量策略之间的距离，并给出了整体的优化公式：
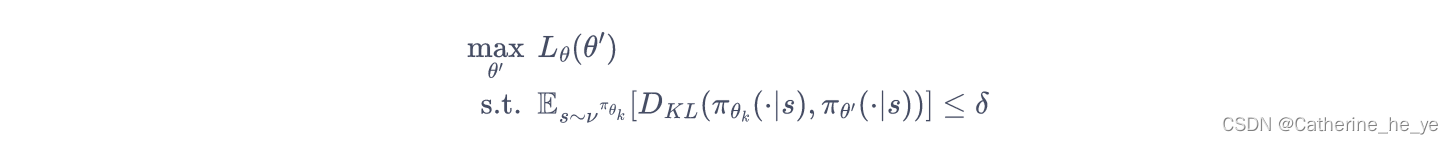这里的不等式约束定义了策略空间中的一个 KL 球，被称为信任区域。在这个区域中，可以认为当前学习策略和环境交互的状态分布与上一轮策略最后采样的状态分布一致，进而可以基于一步行动的重要性采样方法使当前学习策略稳定提升。

1.3. 近似求解

直接求解上式带约束的优化问题比较麻烦，TRPO 在其具体实现中做了一步近似操作来快速求解。
对目标函数和约束在${\theta }_k$进行泰勒展开，分别用 1 阶、2 阶进行近似：
于是我们的优化目标变成了：
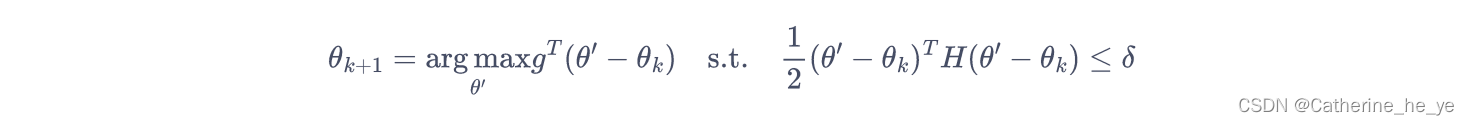此时，我们可以用KKT条件直接导出上述问题的解：

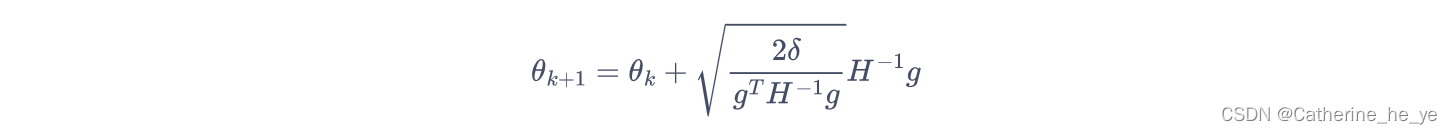
1.4. 共轭梯度

一般来说，用神经网络表示的策略函数的参数数量都是成千上万的，计算和存储黑塞矩阵的逆矩阵会耗费大量的内存资源和时间。

TRPO 通过共轭梯度法（conjugate gradient method）回避了这个问题，它的核心思想是直接计算$x=H^{-1}g$，$x$即参数更新方向。假设满足 KL距离约束的参数更新时的最大步长为$\beta ={\theta }^{\prime }-\theta$。
于是，根据 KL 距离约束条件$\frac{1}{2}({\theta }^{\prime }-{\theta }_k{)}^{T}H({\theta }^{\prime }-{\theta }_k)<=\delta$，有$\frac{1}{2}(\beta x{)}^{T}H(\beta x)=\delta$。求解$\beta$，得到$\beta =\sqrt{\frac{2\delta }{x^{T}Hx}}$。因此，此时参数更新方式为
${\theta }_{k+1}={\theta }_k+\sqrt{\frac{2\delta }{x^{T}Hx}}x$，
因此，只要可以直接计算$x=H^{-1}g$，就可以根据该式更新参数，问题转化为解$Hx=g$。实际上$H$为对称正定矩阵，所以我们可以使用共轭梯度法来求解。
共轭梯度法的具体流程如下：
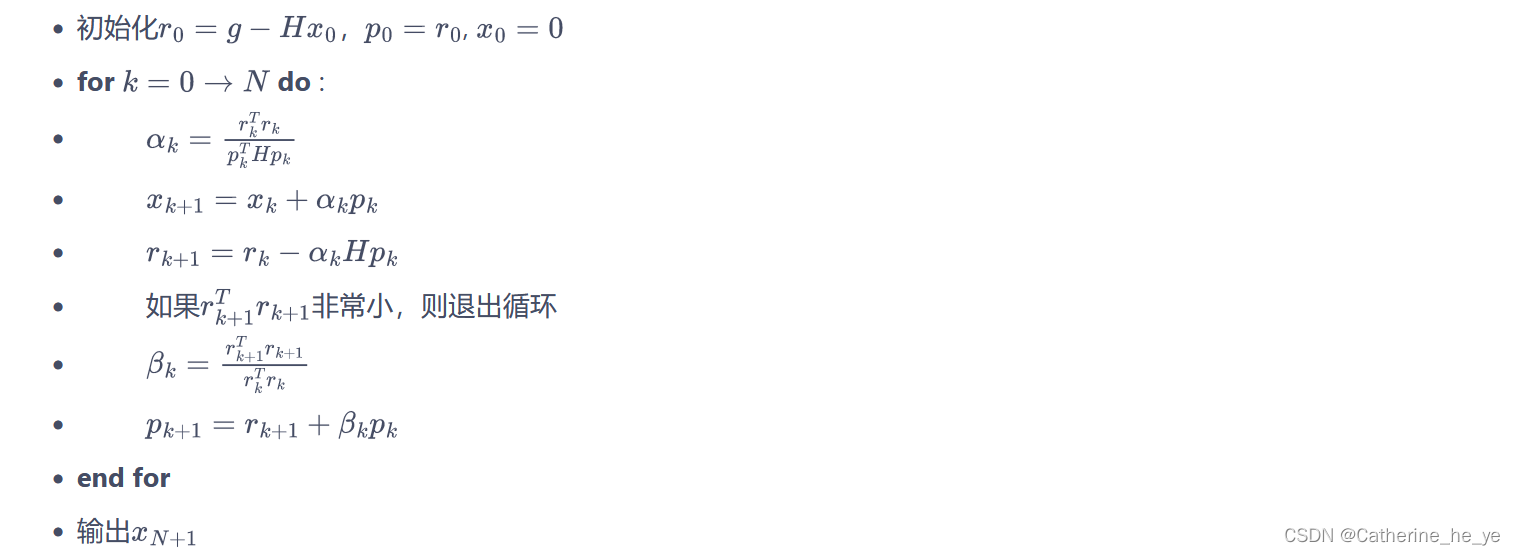在共轭梯度运算过程中，直接计算${\alpha }_k$和$r_{k+1}$需要计算和存储海森矩阵$H$。为了避免这种大矩阵的出现，我们只计算$Hx$向量，而不直接计算和存储$H$矩阵。这样做比较容易，因为对于任意的列向量$v$，容易验证：
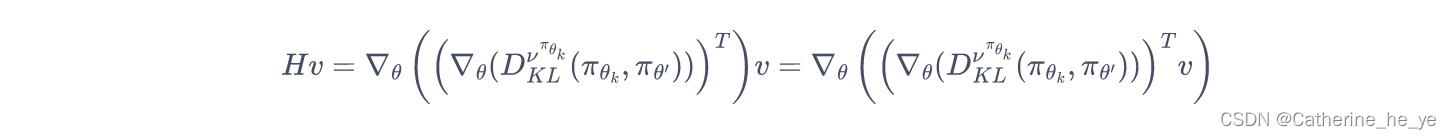即先用梯度和向量$v$点乘后计算梯度。

    def hessian_matrix_vector_product(self, states, old_action_dists, vector):
        # 计算黑塞矩阵和一个向量的乘积
        new_action_dists = torch.distributions.Categorical(self.actor(states))
        kl = torch.mean(
            torch.distributions.kl.kl_divergence(old_action_dists,
                                                 new_action_dists))  # 计算平均KL距离
        kl_grad = torch.autograd.grad(kl,
                                      self.actor.parameters(),
                                      create_graph=True)
        kl_grad_vector = torch.cat([grad.view(-1) for grad in kl_grad])
        # KL距离的梯度先和向量进行点积运算
        kl_grad_vector_product = torch.dot(kl_grad_vector, vector)
        grad2 = torch.autograd.grad(kl_grad_vector_product,
                                    self.actor.parameters())
        grad2_vector = torch.cat([grad.view(-1) for grad in grad2])
        return grad2_vector

    def conjugate_gradient(self, grad, states, old_action_dists):  # 共轭梯度法求解方程
        x = torch.zeros_like(grad)
        r = grad.clone()
        p = grad.clone()
        rdotr = torch.dot(r, r)
        for i in range(10):  # 共轭梯度主循环
            Hp = self.hessian_matrix_vector_product(states, old_action_dists,
                                                    p)
            alpha = rdotr / torch.dot(p, Hp)
            x += alpha * p
            r -= alpha * Hp
            new_rdotr = torch.dot(r, r)
            if new_rdotr < 1e-10:
                break
            beta = new_rdotr / rdotr
            p = r + beta * p
            rdotr = new_rdotr
        return x

1.5. 线性搜索

由于 TRPO 算法用到了泰勒展开的 1 阶和 2 阶近似，这并非精准求解，因此，$\theta$可能未必比${\theta }_k$好，或未必能满足 KL 散度限制。TRPO 在每次迭代的最后进行一次线性搜索，以确保找到满足条件。具体来说，就是找到一个最小的非负整数$i$，使得按照
$${\theta }_{k+1}={\theta }_k+{\alpha }^i\sqrt{\frac{2\delta }{x^{T}Hx}}x$$

求出的${\theta }_{k+1}$依然满足最初的 KL 散度限制，并且确实能够提升目标函数，这KaTeX parse error: Undefined control sequence: \apha at position 1: \̲a̲p̲h̲a̲ ̲\in (0,1)其中是一个决定线性搜索长度的超参数。

1.6. 总结

至此，我们已经基本上清楚了 TRPO 算法的大致过程，它具体的算法流程如下：

2. PPO 算法（Trust Region Policy Optimization）

2.1. 前沿

PPO 算法作为TRPO算法的改进版，但是其算法实现更加简单。并且大量的实验结果表明，与TRPO相比，PPO能学习得一样好（甚至更快），这使得PPO成为非常流行的强化学习算法。如果我们想要尝试在一个新的环境中使用强化学习算法，那么 PPO 就属于可以首先尝试的算法。

PPO 的优化目标与 TRPO 相同，但 PPO用了一些相对简单的方法来求解（TRPO 使用泰勒展开近似、共轭梯度、线性搜索等方法直接求解）。具体来说，PPO 有两种形式，一是 PPO-惩罚，二是 PPO-截断，接下来对这两种形式进行介绍。

2.2. PPO-惩罚

PPO-Penalty用拉格朗日乘数法直接将 KL 散度的限制放进了目标函数中，这就变成了一个无约束的优化问题，在迭代的过程中不断更新 KL 散度前的系数。即：
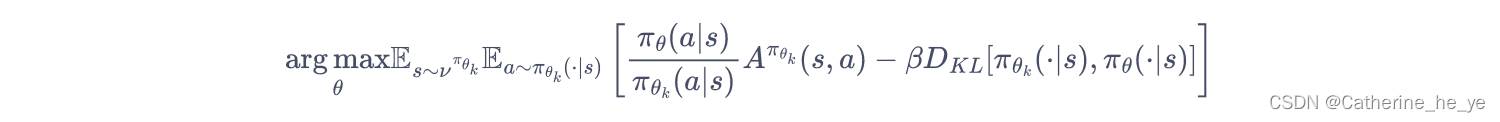令$d_k=D_{KL}^{{\pi }_{{\theta }_k}}({\pi }_{{\theta }_k},{\pi }_{\theta })$，$\beta$的更新规则如下：

1. 如果$d_k<\delta /1.5$，那么${\beta }_{k+1}={\beta }_k/2$
2. 如果$d_k>\delta \times 1.5$，那么${\beta }_{k+1}={\beta }_k\times 2$
3. 否则${\beta }_{k+1}={\beta }_k$

其中，$\delta$是事先设定的一个超参数，用于限制学习策略和之前一轮策略的差距。

2.3 PPO-截断

PPO的另一种形式 PPO-截断（PPO-Clip） 更加直接，它在目标函数中进行限制，以保证新的参数和旧的参数的差距不会太大，即:
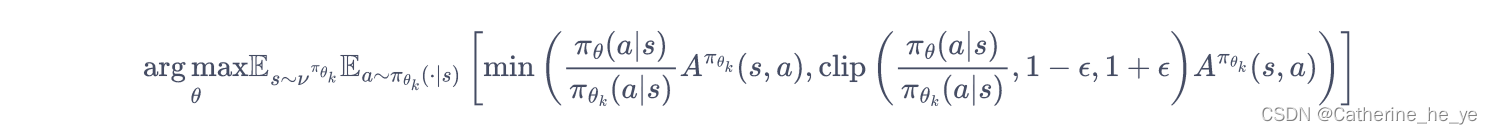其中$clip(x,l,r):=max(min(x,r),l)$ ，即把$x$限制在$[l,r]$内。上式中$ϵ$是一个超参数，表示进行截断（clip）的范围。

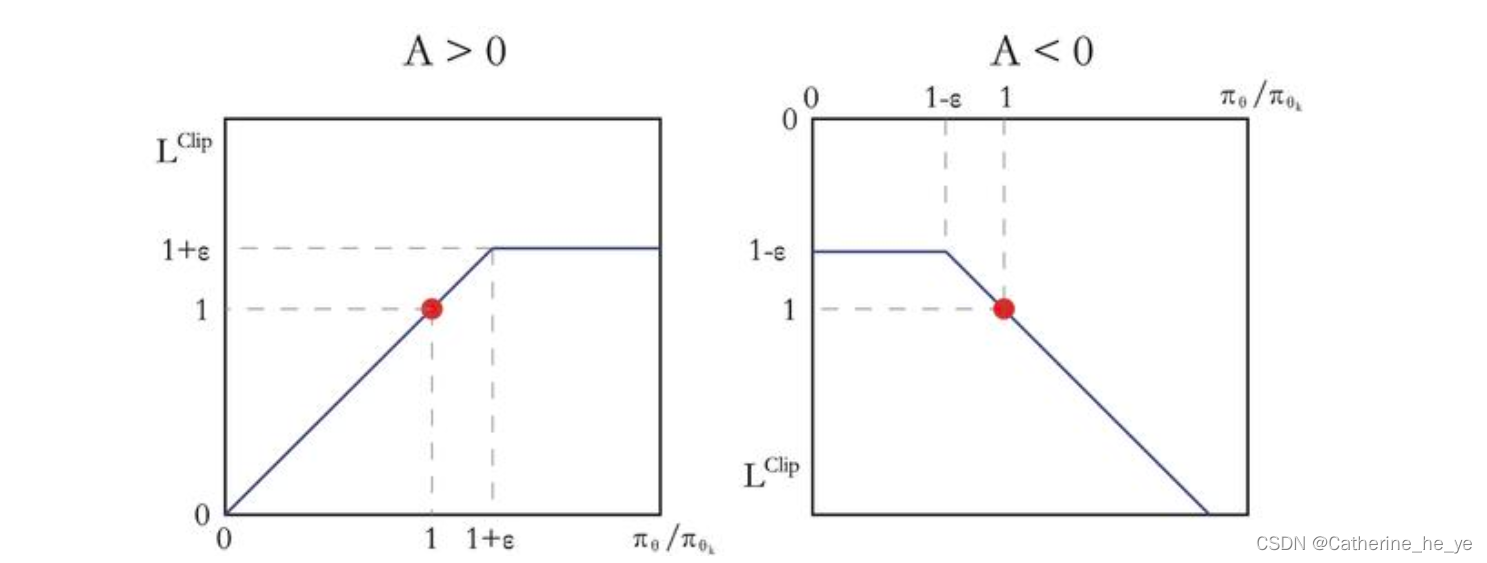
如果$A^{{\pi }_{{\theta }_k}}(s,a)>0$，说明这个动作的价值高于平均，最大化这个式子会增大$\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_k}(a|s)}$，但不会让其超过$1+ϵ$。反之，如果$A^{{\pi }_{{\theta }_k}}(s,a)<0$，最大化这个式子会减小$\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_k}(a|s)}$，但不会让其超过$1-ϵ$。如下图所示。

代码

最后，两个算法的代码可参考GitHub，Good Night!