目录
❤ 断言的功能与语法
❤ 常用断言
❤ 常用的断言表达方式
❤ 异常断言
❤ 正则断言
❤ 检查断言装饰器
❤ 断言的功能与语法
Python assert(断言)用于判断一个表达式,在表达式条件为 False 的时候触发异常
断言可以在条件不满足程序运行的情况下直接返回错误,而不必等待程序运行后出现崩溃的情况
# 用法:
assert exception, message
# 参数:
# exception:表达式,一般是判断相等;或者是判断是某种数据类型的 bool 判断的语句,再决定是否抛出异常
# message:指的是具体的错误信息,选填参数,可以不填写。(但是建议还是填写上)
# 返回值:无返回值(虽然表达式有返回值,但 assert 没有;表达式为 Treu , assert 将不会触发任何异常)
❤ 常用断言
断言方式是自身框架来实现的,即self.assertEqual()等,当我们使用pytest框架后,这种断言方式是不可用的,因为测试类不会再继承unittest.TestCase类,因此pytest使用的断言是使用python内置的断言assert,相对于unittest各种各样的断言方法,但内置的断言会更简洁,它只有一种,如下。
关键代码:assert 表达式, 错误提示信息
def test_login():
# 使用python内置的断言
assert 1 == 2, '1是不等于2的' # 错误信息也可以不写
test_login()运行结果:
C:\software\python\python.exe D:/learn/test.py
Traceback (most recent call last):
File "D:/learn/test.py", line 13, in <module>
test_login()
File "D:/learn/test.py", line 11, in test_login
assert 1 == 2, '1是不等于2的'
AssertionError: 1是不等于2的Process finished with exit code 1
❤ 常用的断言表达方式:
assert xx:判断xx为真assert not xx:判断xx不为真assert a in b:判断b包含aassert a not in b:判断b不包含aassert a == b:判断a等于bassert a != b:判断a不等于b
❤ 异常断言
可以使用pytest.raises作为上下文管理器,当抛出异常时可以获取到对应的异常实例,然后断言它抛出的异常是不是预期的。
# 断言异常
def test_zero_division():
with pytest.raises(ZeroDivisionError):
1 / 0如任意一个自然数除以0时,由于0不能作为被除数,执行时就会抛出ZeroDivisionError异常,提示division by zero
# 详细断言异常
def test_zero_division_long():
with pytest.raises(ZeroDivisionError) as excinfo:
1 / 0
# 断言异常类型 type
assert excinfo.type == ZeroDivisionError
# 断言异常 value 值
assert "division by zero" in str(excinfo.value) 注意:断言type的时候,异常类型是不需要加引号的,断言value值的时候需转str类型
❤ 正则断言
可以将match关键字参数传递给上下文管理器,以测试正则表达式与异常的字符串表示形式是否匹配
注意:这种方法只能断言value,不能断言type
# 自定义消息
def test_zero_division_long():
with pytest.raises(ZeroDivisionError, match=".*zero.*") as excinfo:
1 / 0该match方法的regexp参数 re.search函数匹配,因此在上面的示例中match='zero'也可以使用
# 自定义消息
def test_zero_division_long():
with pytest.raises(ZeroDivisionError, match="zero") as excinfo:
1 / 0运行结果:

❤ 检查断言装饰器
当代码抛出异常时,如果和raises指定的异常类相匹配,就不会断言失败。
它相当于一个检查异常装饰器,目的是检查是否有异常(不确定是否有异常),不同使用场景:
with pytest.raise(ZeroDivisionError)对于故意测试异常代码的情况,使用可能会更好- 而
@pytest.mark.xfail(raises=ZeroDivisionError)对于检查未修复的错误(即可能会发生异常),使用检查断言可能会更好
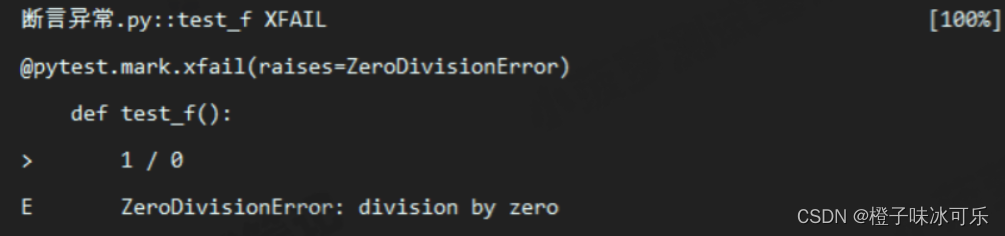
# 断言装饰器
@pytest.mark.xfail(raises=ZeroDivisionError)
def test_f():
1 / 0执行结果: