更新时间:2023-2-19 16:30

相关链接

（1）2023年美赛C题Wordle预测问题一建模及Python代码详细讲解
（2）2023年美赛C题Wordle预测问题二建模及Python代码详细讲解
（3）2023年美赛C题Wordle预测问题三、四建模及Python代码详细讲解
（4）2023年美赛C题Wordle预测问题25页论文

1 问题三

这是 一个聚类分析问题

1.1 特征工程

这部分和问题一的一样

我提取了每个单词中每个字母位置的特征（如a编码为1，b编码为2，c编码为3依次类推，z编码为26，那5个单词的位置就填入相应的数值，类似于ont-hot编码）、元音的字母的频率（五个单词中元音字母出现了几次），辅音字母的频率（5个单词中辅音字母出现了几次），还有一个是单词的词性（形容词，副词，名词等等，这部分没有做）

1.2 模型建立、预测、评价

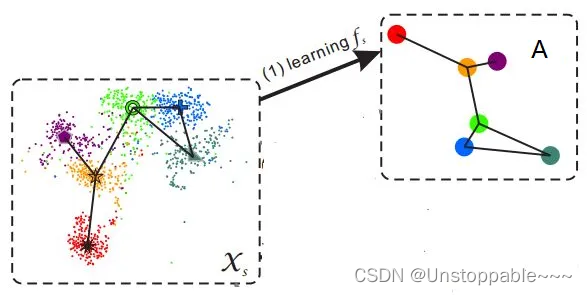
采用层次聚类模型，谱系聚类图绘制如下，可以将图明显的分为两种类别，分别为苦难和简单，说明黄色部分是数量较少，对应游戏的困难程度，绿色对应单词容易程度。

（1）层次聚类的合并算法

层次聚类的合并算法通过计算两类数据点间的相似性，对所有数据点中最为相似的两个数据点进行组合，并反复迭代这一过程。简单的说层次聚类的合并算法是通过计算每一个类别的数据点与所有数据点之间的距离来确定它们之间的相似性，距离越小，相似度越高。并将距离最近的两个数据点或类别进行组合，生成聚类树。

（2）欧几里德距离矩阵

层次聚类使用欧式距离来计算不同类别数据点间的距离（相似度）。我们在前面的几篇文章中都曾经介绍过欧氏距离的计算方法，本篇文章将通过创建一个欧式距离矩阵来计算和对比不同类别数据点间的距离，并对距离值最小的数据点进行组合。以下是欧式距离的计算公式。
$$D=\sqrt{(x1-y1{)}^2+(x2-y2{)}^2}$$

from sklearn.cluster import AgglomerativeClustering #导入sklearn的层次聚类函数
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import linkage,dendrogram
#这里使用scipy的层次聚类函数
Z = linkage(Train, method = 'ward', metric = 'euclidean') #谱系聚类图
P = dendrogram(Z, 0) #画谱系聚类图
# plt.savefig('img/AGG层次聚类.png',dpi=300)
plt.show()

将聚类分为两类并可视化到二维如下，并计算评价聚类效果的指标，轮廓系数。得分聚类轮廓系数为：0.22768071822489375。

import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score
from sklearn.decomposition import PCA
from sklearn.cluster import AgglomerativeClustering #导入sklearn的层次聚类函数
data1 = Train

clf1 = AgglomerativeClustering(n_clusters = 2, linkage = 'ward')
s = clf1.fit(data1)
pred1 = clf1.fit_predict(data1)
score1 = silhouette_score(data1, pred1)
print(f'聚类轮廓系数为：{score1}')
pca = PCA(n_components=2)  # 输出两维
newData1 = pca.fit_transform(data1)  # 载入N维

x1, y1 = [], []
x2, y2= [], []
x3, y3= [], []
# 0表示简单，1表示困难
for index, value in enumerate(pred1):
    if value == 0:
        x1.append(newData1[index][0])
        y1.append(newData1[index][1])
    elif value == 1:
        x2.append(newData1[index][0])
        y2.append(newData1[index][1])
plt.figure(figsize=(10, 10))

# #定义坐标轴
k = 200
plt.scatter(x1, y1,s=k)
plt.scatter(x2, y2,s=k)
plt.scatter(x3, y3,s=k)
plt.legend(['Hard','Easy'])
plt.savefig('img/2.png',dpi=300)
plt.show()

将模型输入EERIE的特征后，输出是困难。

模型验证：手动给数据集标注，将1-4次尝试的百分比，归一化后求和，如果大于0.6标注为困难，小于0.6标注为简单。将聚类类别结果和手动标注的类别进行计算准确率，准确率有0.73。

2 问题四

（1）分析了Number in hard mode趋势

（2）分析了几种百分比的占比情况

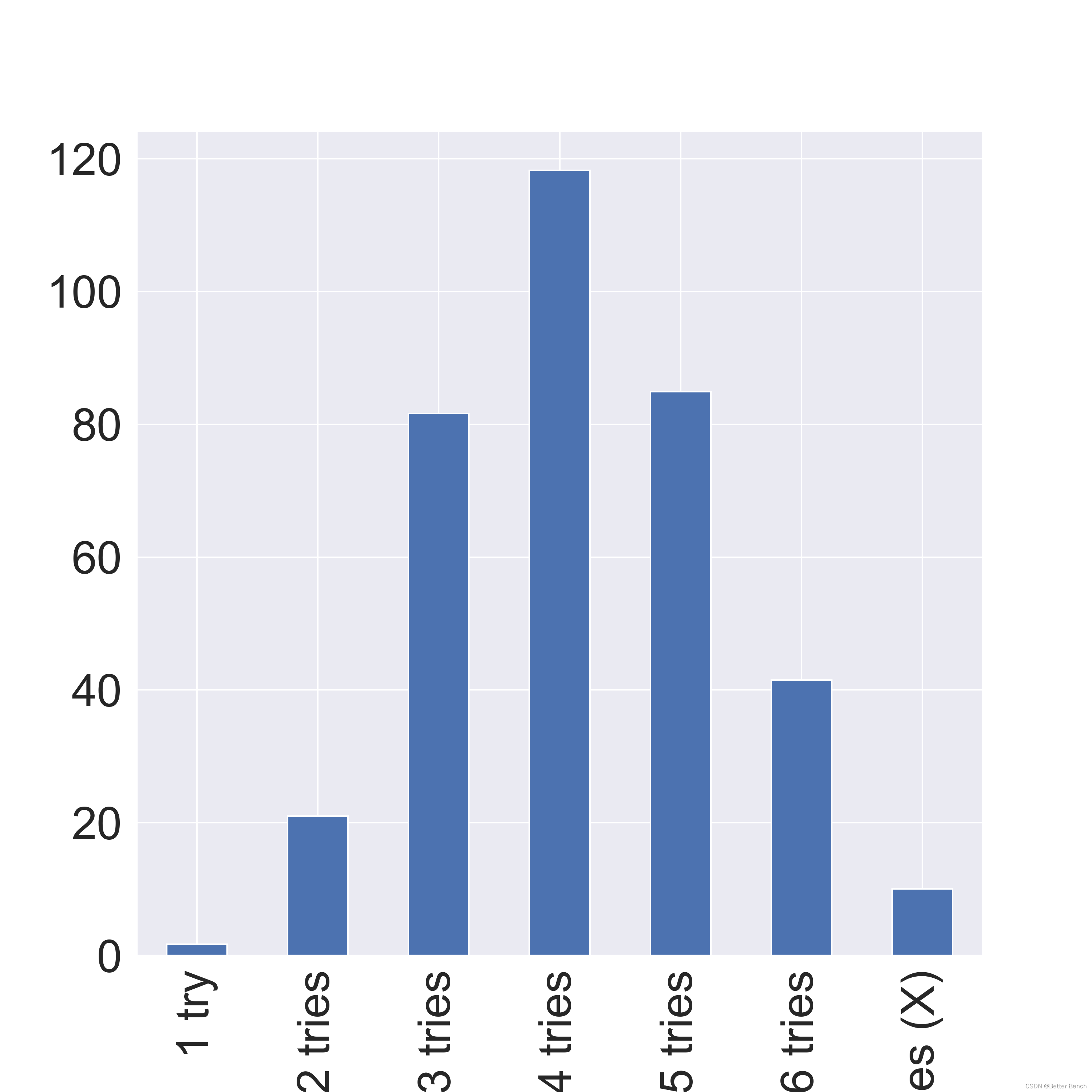
3 Code

Code获取，在浏览器中输入：betterbench.top/#/40/detail，或者Si我
1

剩下的问题一、二、三、四代码实现，在我主页查看，其他文章，或者在此文章的顶部点击查看。