文章目录

• • 4.1 概述
  • 4.2 有穷状态机
  • 4.3 Petri网
  • 4.4 Z语言

---

• 按照形式化程度，可以把软件工程使用的方法划分成非形式化、半形式化、形式化三类
• 非形式化方法：使用自然语言描述需求规格说明
• 半形式化方法：使用数据流图或实体-联系图建立模型
• 形式化方法：描述系统性质的基于数学的技术，即有坚实的数学基础的方法就是形式化方法

4.1 概述

• 非形式化方法的缺点
  • （1）矛盾，一组相互冲突的描述；
  • （2）二义性，读者可有不同的理解；
  • （3）含糊性，说明不清楚；
  • （4）不完整性；
  • （5）抽象层次混乱，非常抽象的陈述中有关于细节的低层陈述。
  • 【注意】用自然语言描述需求规格说明，是典型的非形式化方法。
• 形式化方法的优点
  • （1）能保证规格说明中尽可能没有矛盾、二义性、含糊性和不完整性。
  • （2）可以在不同的软件工程活动之间平滑地过渡。
  • （3）提供了高层确认的手段，可以使用数学方法进行证明验证。
• 形式化方法的缺点
  • （1）难于表示问题的时序、控制和行为等方面的需求。
  • （2）相比欠形式化方法，它更难学习，培训的投资过大。
  • 【注意】如果一种方法有坚实的数学基础，那么它就是形式化的。
• 应用形式化方法的准则
  • （1）应该选用适当的表示方法。
  • （2）应该形式化，但不要过分形式化。
  • （3）应该估算成本。
  • （4）应该有形式化方法顾问随时提供咨询。
  • （5）不应该放弃传统的开发方法。
  • （6）应该建立详尽的文档。
  • （7）不应该放弃质量标准。
  • （8）不应该盲目依赖形式化方法。
  • （9）应该测试、测试再测试。
  • （10）应该重用。

4.2 有穷状态机

• 概念
  • （1）定义
    • 有穷状态机是表达规格说明的一种形式化方法。
  • （2）构成
    • 一个有穷状态机包括下述5个部分：状态集J、输入集K、由当前状态和当前输入确定下一个状态（次态）的转换函数T、初始态S和终态集F。一个有穷状态机可以表示为一个5元组（J，K，T，S，F）。其中：J是一个有穷的非空状态集；K是一个有穷的非空输入集；T是一个从(J-F)×K到J的转换函数；S∈J，是一个初始状态；F⊆J，是终态集。
  • （3）状态转换形式
    • 当前状态[菜单]＋事件[所选择的项]⇒下个状态
  • （4）谓词集P
    • ① 谓词集P把有穷状态机扩展为一个6元组，其中每个谓词都是系统全局状态Y的函数。
    • ② 加入谓词集后转换规则形式为：当前状态[菜单]＋事件[所选择的项]＋谓词⇒下个状态。
• 评价
  • （1）优点
    • ① 采用易于书写、易于验证的格式来描述规格说明，能容易地把规格说明转变成设计或程序代码。
    • ② 比数据流图技术更精确且易于理解。
  • （2）缺点
    • ① 在开发一个大系统时，三元组（即状态、事件、谓词）的数量会迅速增长。
    • ② 形式化的有穷状态机方法没有处理定时需求。

4.3 Petri网

• 概念
• （1）构成
  • ① 一般构成
    • Petri网包含4种元素：一组位置P、一组转换T、输入函数I，以及输出函数O。如图4-1为Petri网的实例。
    • 
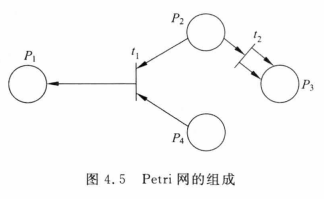
    • a.一组位置P为{P1，P2，P3，P4}，在图中用圆圈代表位置。
    • b.一组转换T为{T1，T2}，在图中用短直线表示转换。
    • c.两个用于转换的输入函数，用由位置指向转换的箭头表示，它们是：
      • I(t1)={P2，P4}
      • I(t2)={P2}
    • d.两个用于转换的输出函数，用由转换指向位置的箭头表示，它们是：
      • O(t1)={P1}
      • O(t2)={P3，P3}
    • 【注意】输出函数O(t2)中有两个P3，是因为有两个箭头由t2指向P3。
  • ② 形式化的Petri网
    • 更形式化的Petri网结构是一个四元组：
    • C=(P，T，I，O)
    • 其中：
      • a.P={P1，…，Pn}是一个有穷位置集，n≥0。
      • b.T={t1，…，tm}是一个有穷转换集，m≥0，且T和P不相交。
      • c．I：T→P^∞为输入函数，是由转换到位置无序单位组（bags）的映射。
      • d．O：T→P^∞为输出函数，是由转换到位置无序单位组的映射。
• （2）作用
  • 用于确定系统中隐含的定时问题，可以有效地描述并发活动。

4.4 Z语言

• 组成部分
  • （1）给定的集合；
  • （2）状态定义；
  • （3）初始状态；
  • （4）操作。
• 优点
  • （1）可以比较容易地发现用Z写的规格说明的错误；
  • （2）使用Z写规格说明时对精确性要求高，减少了模糊性、不一致性和遗漏；
  • （3）可以降低软件开发费用；
• 用Z写规格说明，更加清楚和正确。