上一节我们讲到了退化圈方向搜索算法,它能得到全局最优解。然而算法运行过程中需要选择一个可行改进圈方向,对于一个大型网络流来说,这并非容易的。我们需要找到在每次循环中确认可行改进圈方向或者证明不存在的方法。我们现在就来探讨这个问题
传送门:网络流与图(一)
1
最优流消圈算法
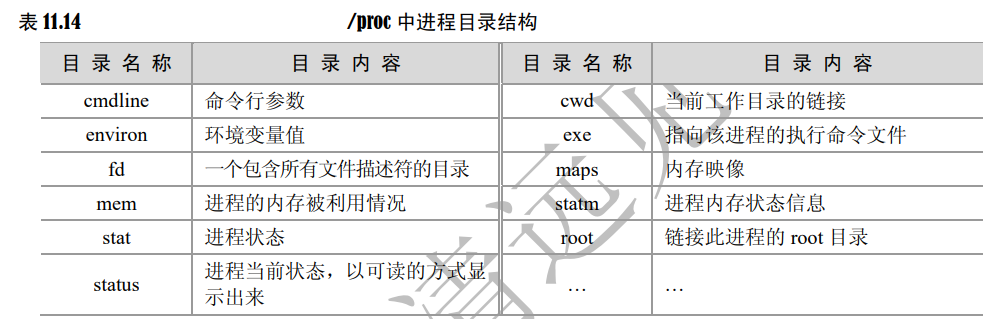
首先,我们需要定义残留有向图(residual digraph):

举个例子,对于下面弧上数字表示费用、容量和流量的网络图,构建的残留有向图为:
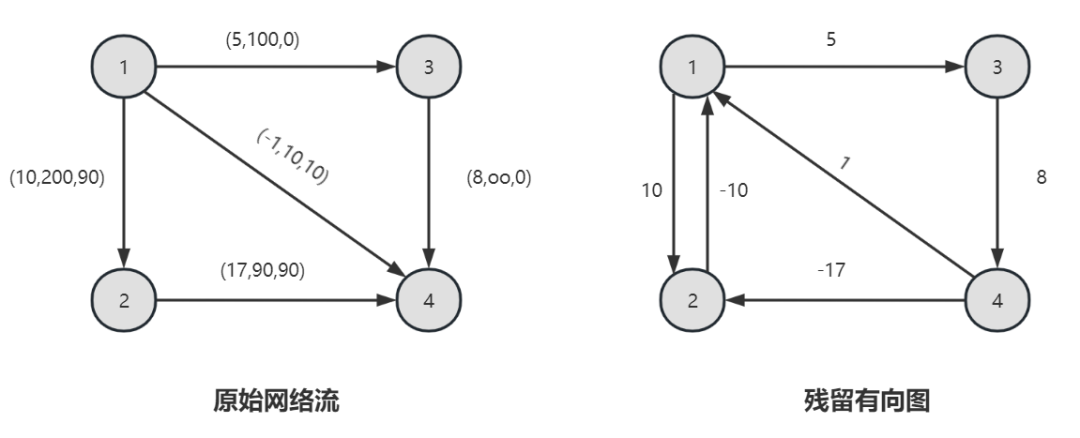
残留有向图构建的意义在于可以确认可行改进圈方向,只需要满足:

这样,我们只需要确定残留有向图是否存在负回路就能判断可行改进圈方向。回忆一下,在最短路径规划章节里,我们提到弗洛伊德-瓦尔肖算法也可用于检验网络流中是否存在负回路。
将弗洛伊德-瓦尔肖算法应用于当前可行流对应的残留有向图:可能会得到一条负回路,即说明原始图中对应圈的方向可行改进;也可能会完成一次最短路计算,即证明可行改进圈方向不存。
对上面例子应用弗洛伊德-瓦尔肖算法,直接执行代码得到结果:
传送门:最短路与动态规划(二)
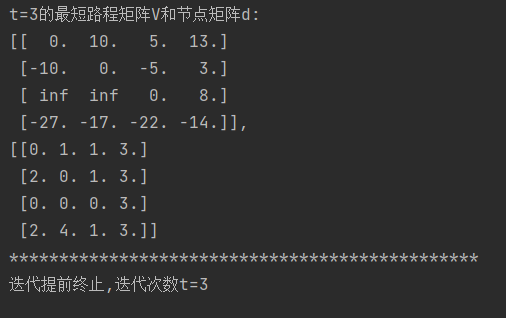
v[4,4]=-14,存在一条负回路,回溯可得其负回路:4-2-1-3-4。该路就是对应原始图的可行改进圈方向。
至此,我们可以得到网络流消圈算法:

回到OOI案例,我们应用网络流消圈算法,看看具体的过程。
t=0时刻,原始图与残留有向图为:
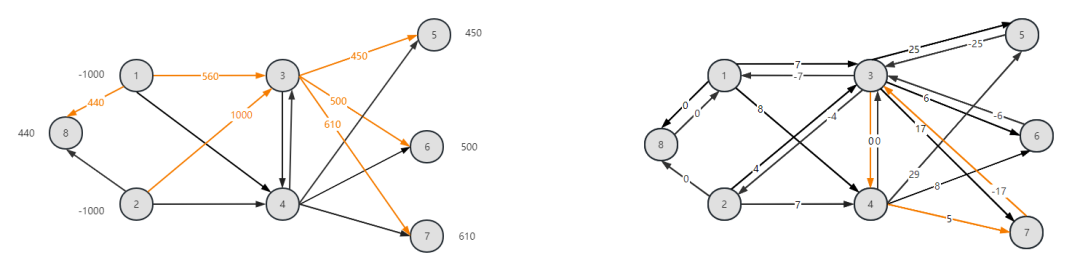
得到负权环路7-3-4-7,c=-12,λ=25。往下迭代,
t=1时刻,原始图与残留有向图为:
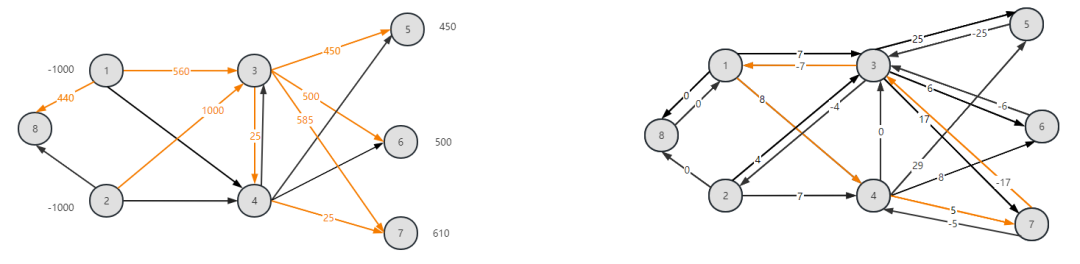
得到负权环路7-3-1-4-7,c=-11,λ=560。往下迭代,
t=2时刻,原始图与残留有向图为:
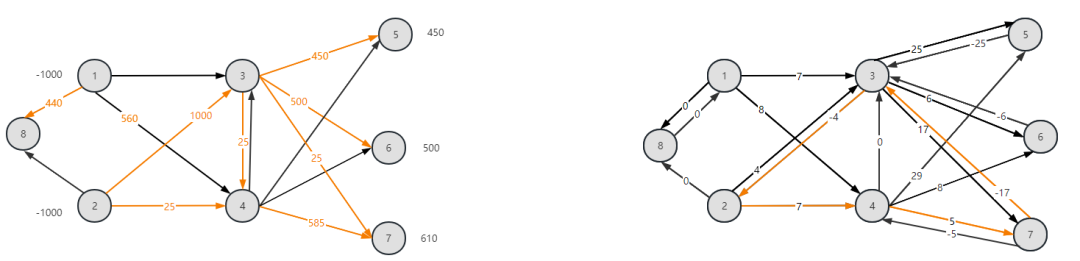
得到负权环路7-3-2-4-7,c=-9,λ=25。往下迭代,
t=3时刻,原始图与残留有向图为:
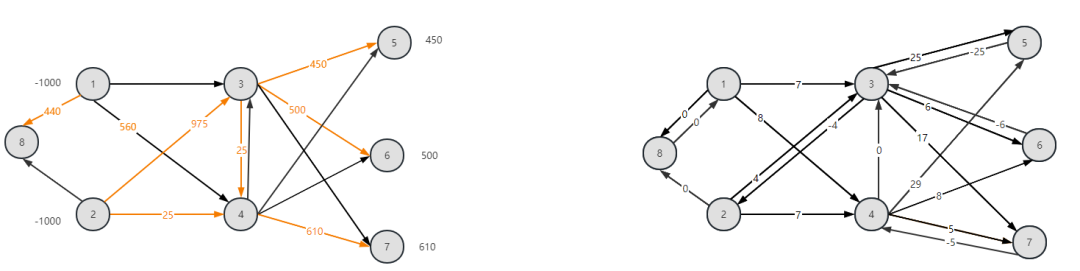
残留有向图不存在负权回路,模型最优!
2
网络单纯圈形法
迄今为止,讨论的最小费用网络流模型都是线性规划问题,我们知道解决此问题还有单纯形法。这一节我们利用单纯形方向开发网络单纯圈形法(network simplex).
考虑OOI项目的圈2-3-1-4-2:
图中包含该圈的节点-弧关联矩阵对应列为:
假设我们对圈中前向弧对应的列向量赋予权重+1,后向弧权重赋予-1,则:

意味着这些列是线性相关的,因为任意一个向量可以被其他向量非零线性组合表示。我们得到一个知识:表示圈中弧的节点-弧关联列会形成一个线性相关集合
由于单纯形法的初始基要求是线性独立的,我们马上得到一个结论:
在最小费用网络流模型中,基弧集合不能包含圈;且每个线性相关弧集都包含一个圈
接下来我们继续引入其他概念,若一个图的每对节点间都存在一条链,则称该图是连通的(connected)。若一个图是连通的且不包含圈,则它是一个树(tree)。若一个树连接了图中每个节点,则它是一个生成树(spanning tree)。
下面展示了一些例子。

我们还知道,基必须是一个最大线性独立集。对生成树中插入任意一个其他弧都会形成一个圈,这样就形成了线性相关集。于是我们很快得到:生成树对应着最大线性独立集和基。
在最小费用网络流问题的节点-弧关联矩阵中,一个列集会形成一个基,当且仅当其对应的弧能够形成相关有向图的一个生成树。
接下来只需要确定单纯形的初始基解和单纯圈方向即可。单纯圈方向非常容易确定,只需要增加零流量非基弧上的流量所形成的圈即可。
在网络流问题的基解下,非基弧上的流量等于0或容量u。基弧上的流量是唯一确定的,能够在特点的非基值下实现流平衡。若所有基弧上的流量都在界限之内,则该流是基可行的。
举个例子,对于下面OOI的初始基解:
有数字部分当前可行流,红色部分是对应的生成树,即表示初始基可行流。对于每个非基弧,找到对应的单纯形方向:
最后选择改进的单纯圈方向进行改进即可。至此,我们得到网络单纯搜索算法:

应用该算法,得到上面OOI案例的迭代过程。
t=0时刻,单纯形方向选择(2,4),单纯圈为2-4-1-8-2,步长为75,得到:
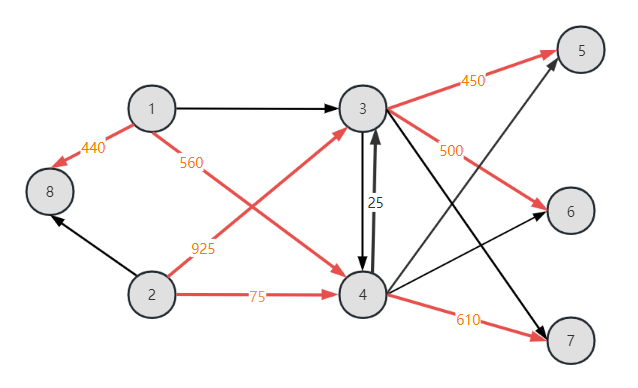
设置t=1,寻找非基弧对应的单纯形方向:
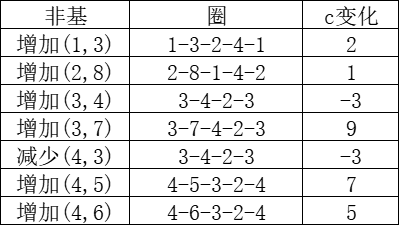
单纯形方向选择(3,4),单纯圈为3-4-2-3,步长为25,得到:
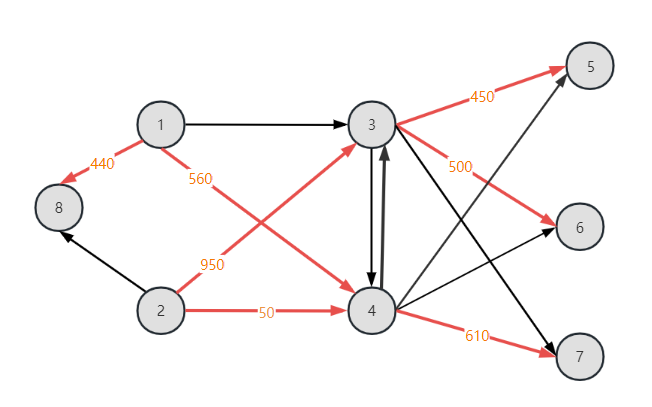
设置t=2,寻找非基弧对应的单纯形方向:
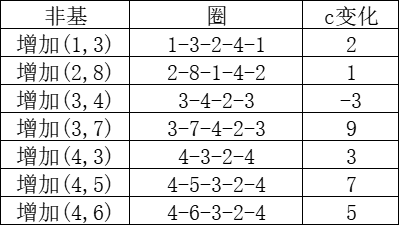
单纯形方向选择(3,4),单纯圈为3-4-2-3,步长为25,得到:
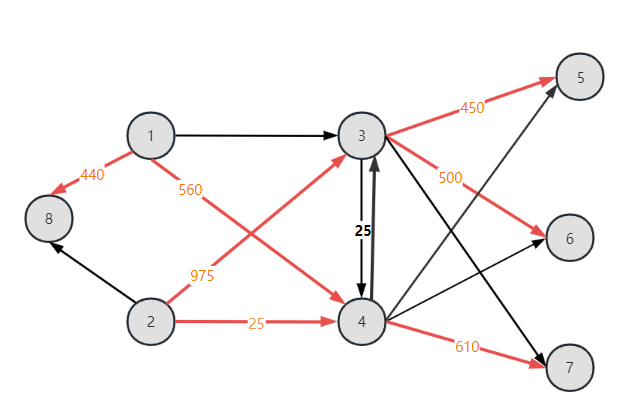
设置t=3,此时不存在改进单纯形方向,迭代停止。