简介

本博客用多元线性回归展示如何从零实现一个随机梯度下降SGD, 不使用torch等AI框架

问题建模

给定一个数据集$X\in {\mathbb{R}}^{N\times (D+1)}$和对应标签向量$Y\in {\mathbb{R}}^N$, 权重为$W\in {\mathbb{R}}^{D+1}$(包含${\omega }_0$), 其中$N$为数据集规模, $D$为样本特征维度.

则预测的标签$\hat{Y}$为:
$$\hat{Y}=XW$$
误差函数采用均方差MSE, 即$\ell$为
$$\ell (W)=\frac{|\hat{Y}-Y{|}_2}{2N}=\frac{|XW-Y{|}_2}{2N}$$
根据梯度下降理论, 误差函数$\ell (W)$求导为:
$$\begin{gathered} \frac{\partial }{\partial W}\ell (W)=\frac{\partial }{\partial W}\frac{|XW-Y{|}_2}{2N} \\ =\frac{\partial }{\partial W}\frac{|XW-Y{|}^2}{2N} \\ =\frac{\partial }{\partial (W)}\frac{(XW-Y{)}^T(XW-Y)}{2N} \\ =\frac{\partial }{\partial (W)}\frac{W^T{X}^{T}XW-W^T{X}^{T}Y-Y^{T}XW+Y^{T}Y}{2N} \\ =\frac{X^T(XW-Y)}{N} \end{gathered}$$
此处理想情况下, 可以直接令导数$\frac{\partial }{\partial W}\ell (W)=0$, 解得$W$的解析解为$W=(X^{T}X{)}^{-1}{X}^{T}Y$. 但是实际场景中, 由于噪声或者样本规模太少等问题, $X^{T}X$不一定是个可逆矩阵, 因此梯度下降是一个普遍的替代方法.

数据加载和预处理

数据加载

采用房价数据集, 从sklearn下载

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split


X, Y = fetch_california_housing(return_X_y=True)
X.shape, Y.shape	# (20640, 8), (20640, )

预处理

需要对样本$X$增加一列全1的数据, 为了方便划分batch, 然后划分成训练集和测试集.

ones = np.ones(shape=(X.shape[0], 1))
X = np.hstack([X, ones])
validate_size = 0.2
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=validate_size, shuffle=True)

分batch

这里写一个函数, 每次返回一个batch的样本, 为节省内存空间, 采用生成器的形式

def get_batch(batchsize: int, X: np.ndarray, Y: np.ndarray):
    assert 0 == X.shape[0]%batchsize, f'{X.shape[0]}%{batchsize} != 0'
    batchnum = X.shape[0]//batchsize
    X_new = X.reshape((batchnum, batchsize, X.shape[1]))
    Y_new = Y.reshape((batchnum, batchsize, ))

    for i in range(batchnum):
        yield X_new[i, :, :], Y_new[i, :]

损失函数

def mse(X: np.ndarray, Y: np.ndarray, W: np.ndarray):
    return 0.5 * np.mean(np.square(X@W-Y))

def diff_mse(X: np.ndarray, Y: np.ndarray, W: np.ndarray):
    return X.T@(X@W-Y) / X.shape[0]

训练

首先定义超参数

lr = 0.001          # 学习率
num_epochs = 1000   # 训练周期
batch_size = 64     # |每个batch包含的样本数
validate_every = 4  # 多少个周期进行一次检验

定义训练函数

def train(num_epochs: int, batch_size: int, validate_every: int, W0: np.ndarray, X_train: np.ndarray, Y_train: np.ndarray, X_test: np.ndarray, Y_test: np.ndarray):
    loop = tqdm(range(num_epochs))
    loss_train = []
    loss_validate = []
    W = W0
    # 遍历epoch
    for epoch in loop:
        loss_train_epoch = 0
        # 遍历batch
        for x_batch, y_batch in get_batch(64, X_train, Y_train):
            loss_batch = mse(X=x_batch, Y=y_batch, W=W)
            loss_train_epoch += loss_batch*x_batch.shape[0]/X_train.shape[0]
            grad = diff_mse(X=x_batch, Y=y_batch, W=W)
            W = W - lr*grad

        loss_train.append(loss_train_epoch)
        loop.set_description(f'Epoch: {epoch}, loss: {loss_train_epoch}')

        if 0 == epoch%validate_every:
            loss_validate_epoch = mse(X=X_test, Y=Y_test, W=W)
            loss_validate.append(loss_validate_epoch)
            print('============Validate=============')
            print(f'Epoch: {epoch}, train loss: {loss_train_epoch}, val loss: {loss_validate_epoch}')
            print('================================')
    plot_loss(np.array(loss_train), np.array(loss_validate), validate_every)

运行

W0 = np.random.random(size=(X.shape[1], ))  # 初始权重
train(num_epochs=num_epochs, batch_size=batch_size, validate_every=validate_every, W0=W0, X_train=X_train, Y_train=Y_train, X_test=X_test, Y_test=Y_test)

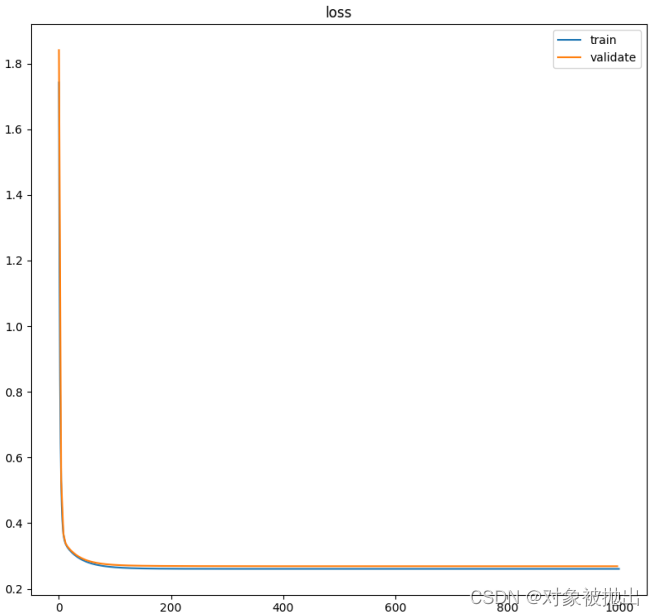
结果如下:

最后画一下损失函数图:

from matplotlib import pyplot as plt
def plot_loss(loss_train: np.ndarray, loss_val: np.ndarray, validate_every: int):
    %matplotlib
    x = np.arange(0, loss_train.shape[0], 1)
    plt.plot(x, loss_train, label='train')
    x = np.arange(0, loss_train.shape[0], validate_every)
    plt.plot(x, loss_val, label='validate')
    plt.legend()
    plt.title('loss')
    plt.show()