一、多元线性回归

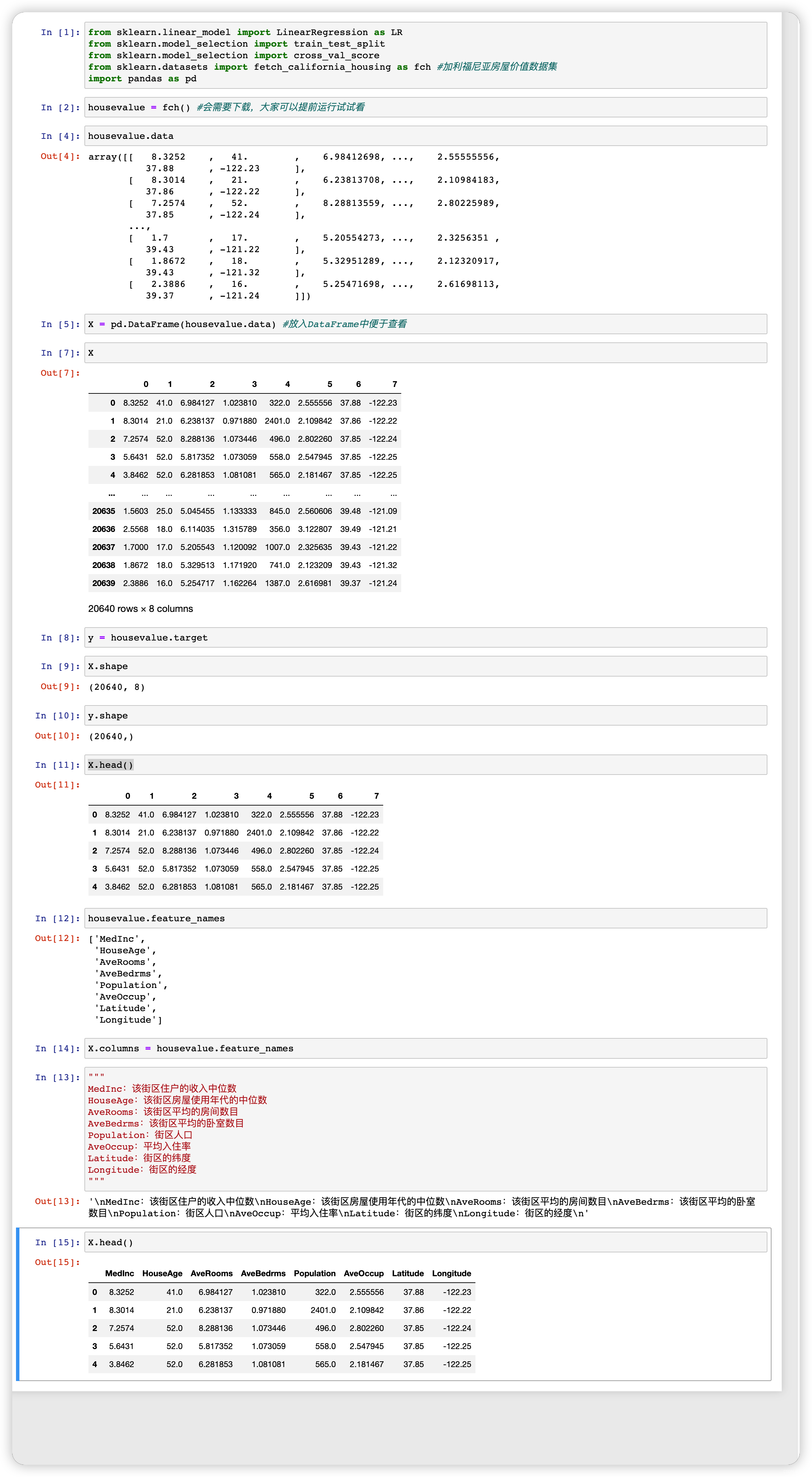
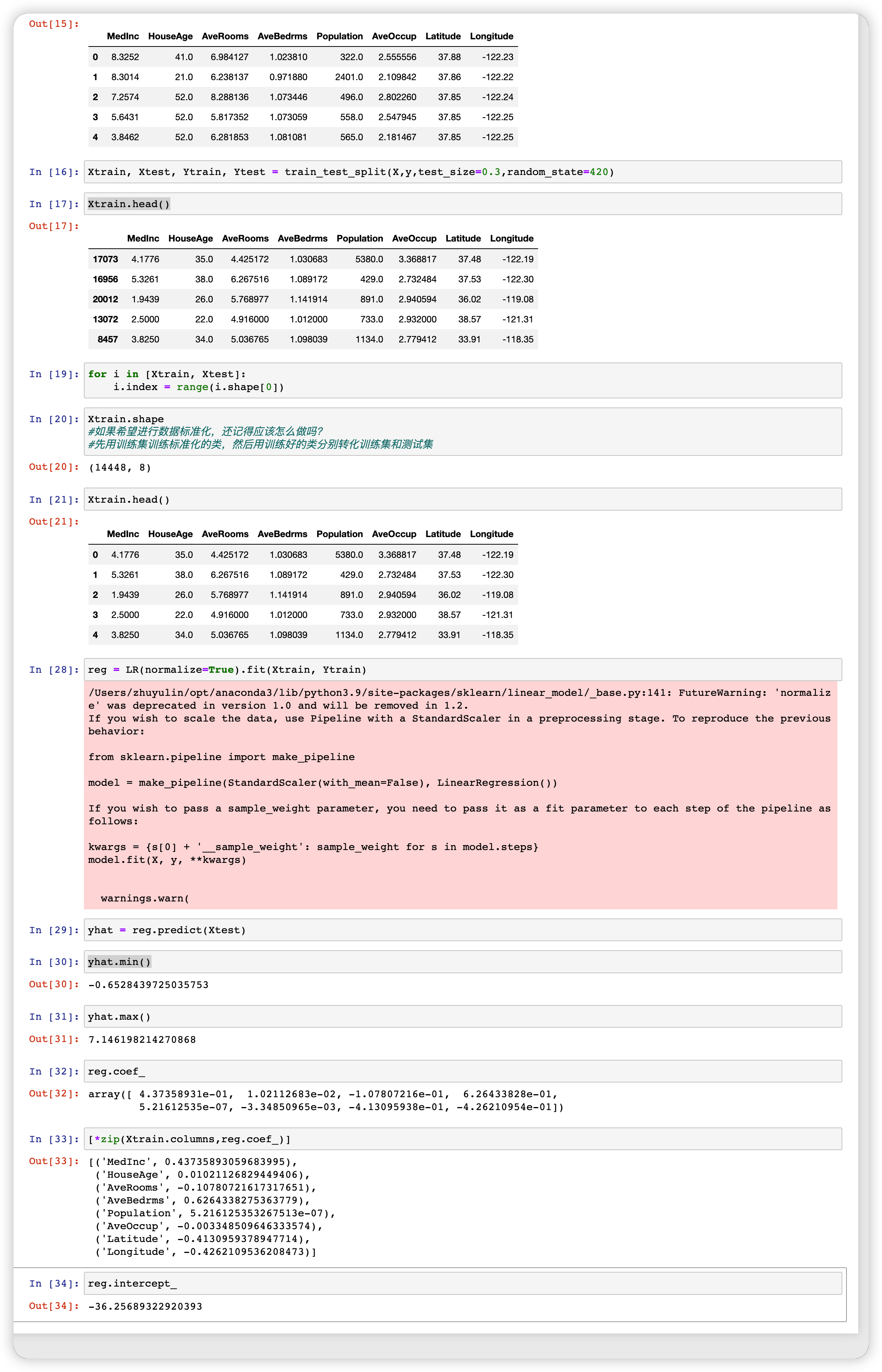
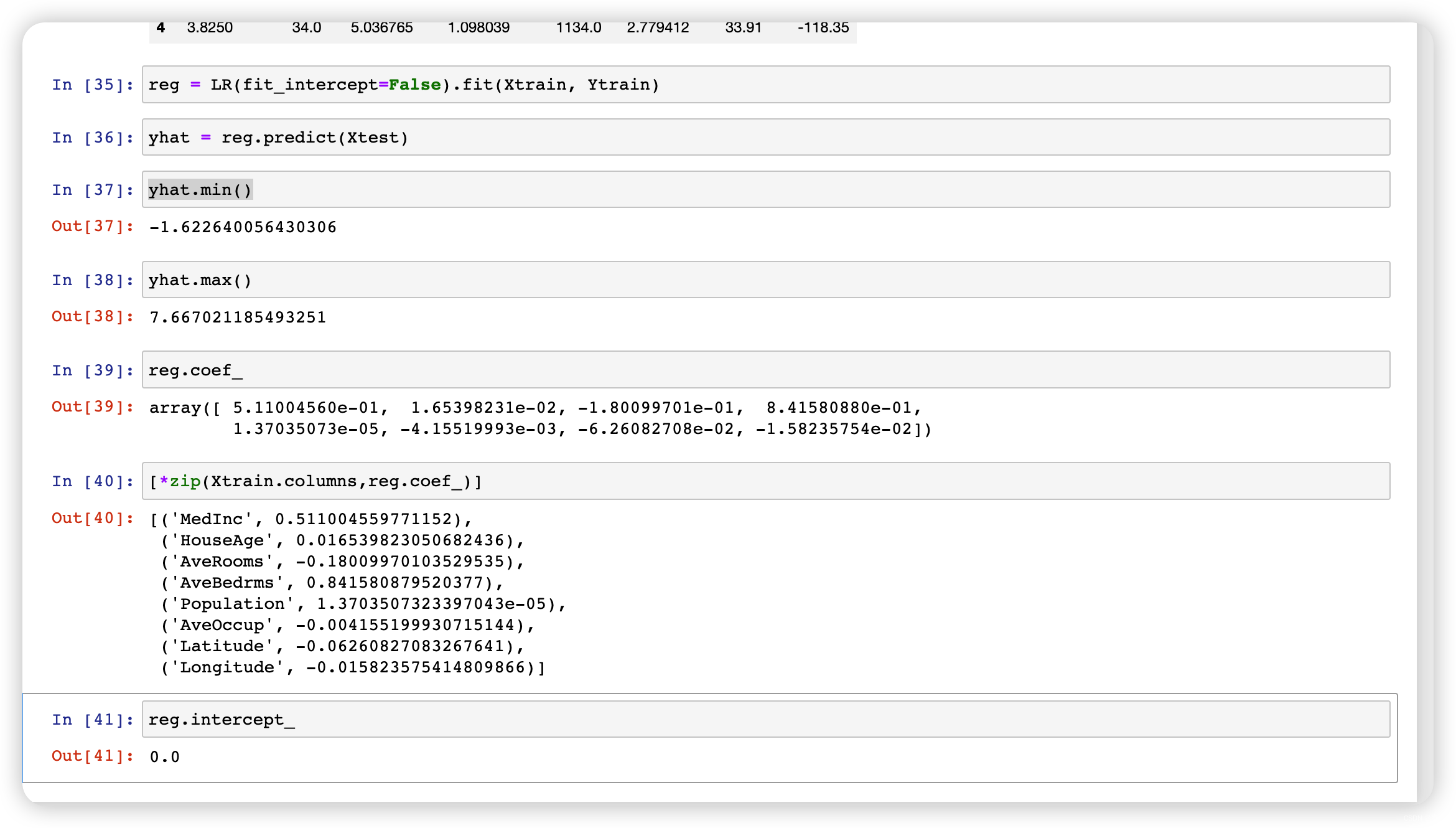
二、回归类的评估指标

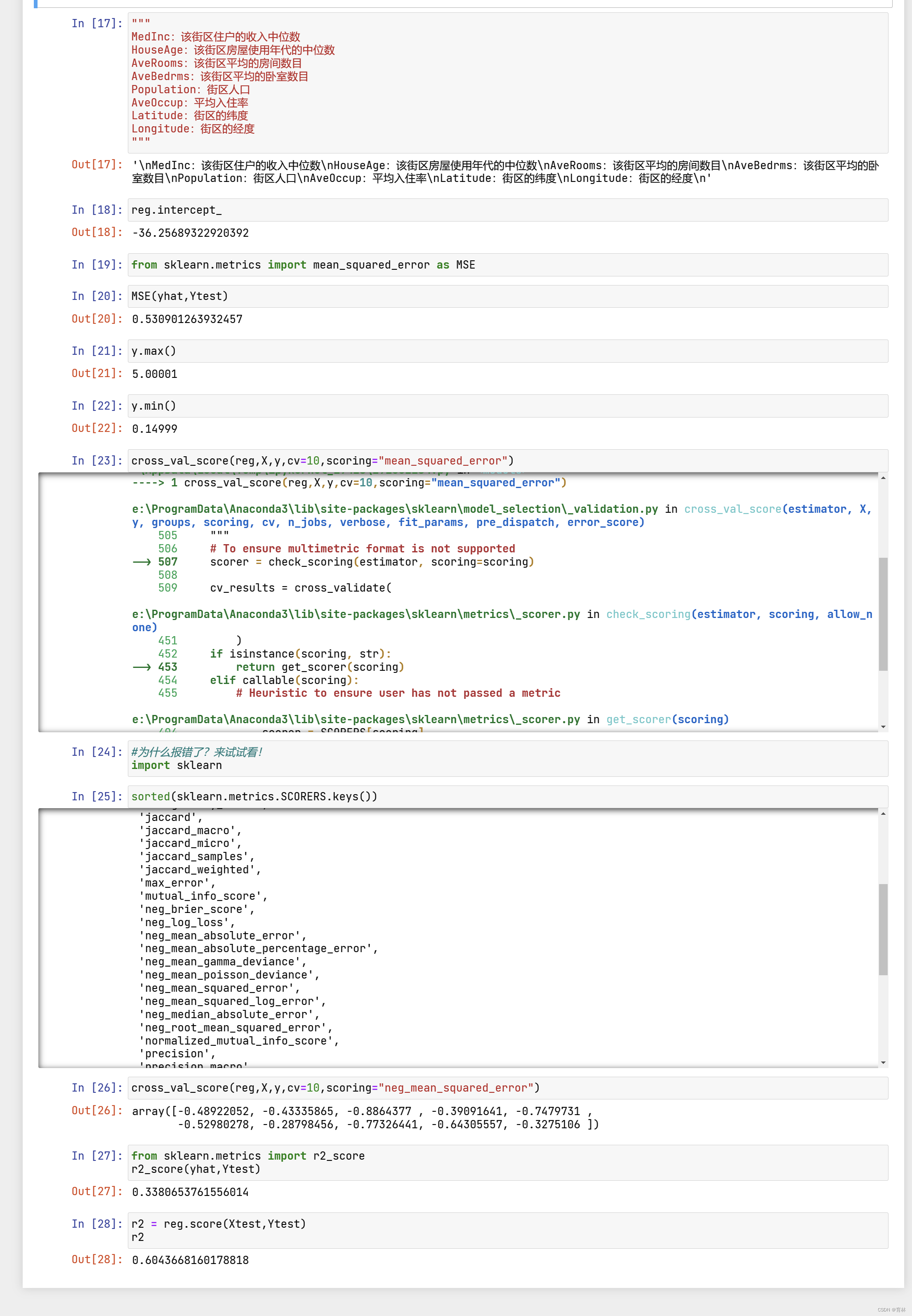
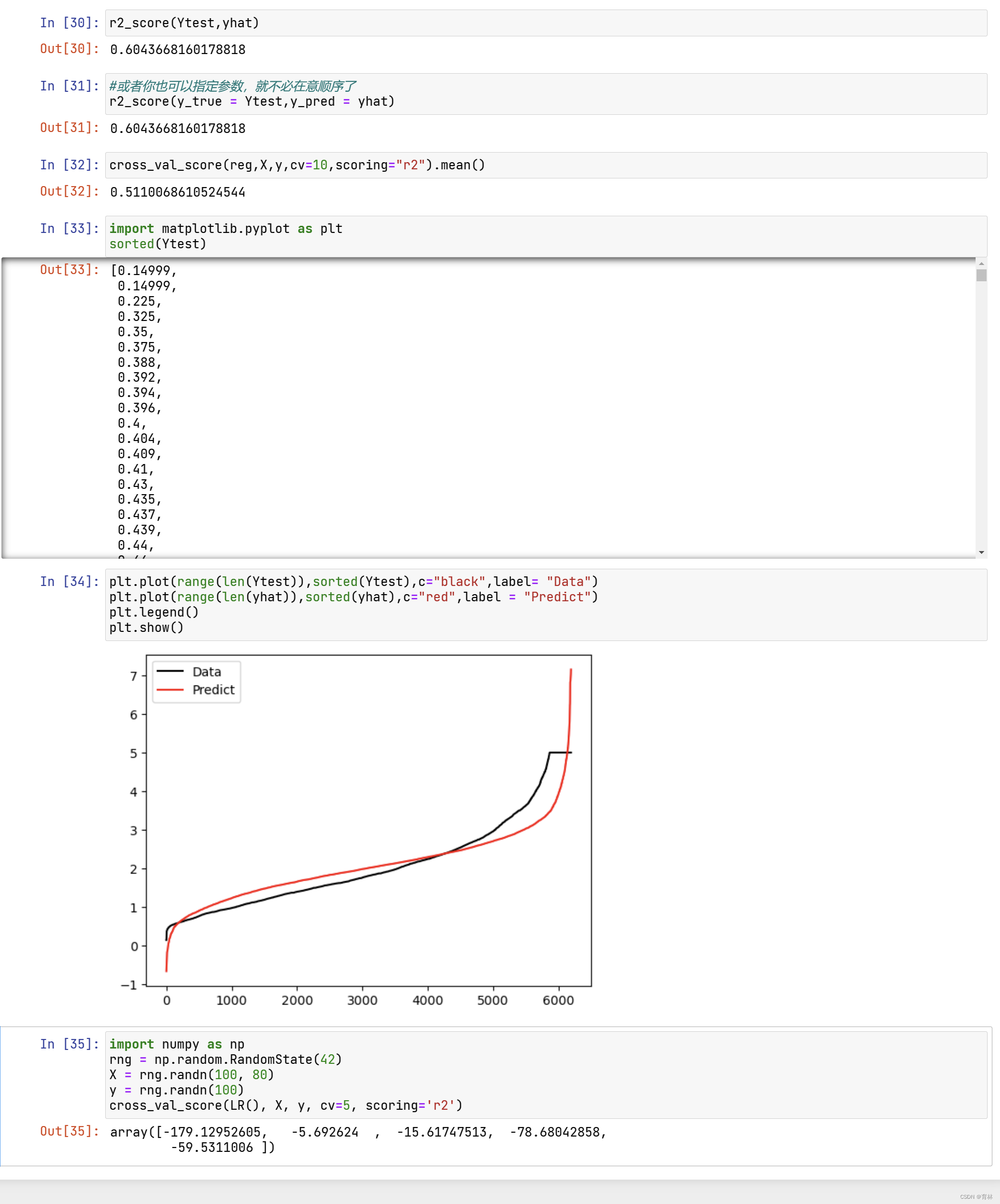
三、多重共线性：岭回归和Lasso

多重共线性 Multicollinearity 与 相关性 Correlation:
多重共线性是一种统计现象，是指线性模型中的特征（解释变量）之间由于存在精确相关关系或高度相关关系，多重共线性的存在会使模型无法建立，或者估计失真。多重共线性使用指标方差膨胀因子（variance inflation factor，VIF）来进行衡量（from statsmodels.stats.outliers_influence import variance_inflation_factor），通常当我们提到“共线性”，都特指多重共线性。
相关性是衡量两个或多个变量一起波动的程度的指标，它可以是正的，负的或者0。当我们说变量之间具有相关性，通常是指线性相关性，线性相关一般由皮尔逊相关系数进行衡量，非线性相关可以使用斯皮尔曼相关系数或者互信息法进行衡量。

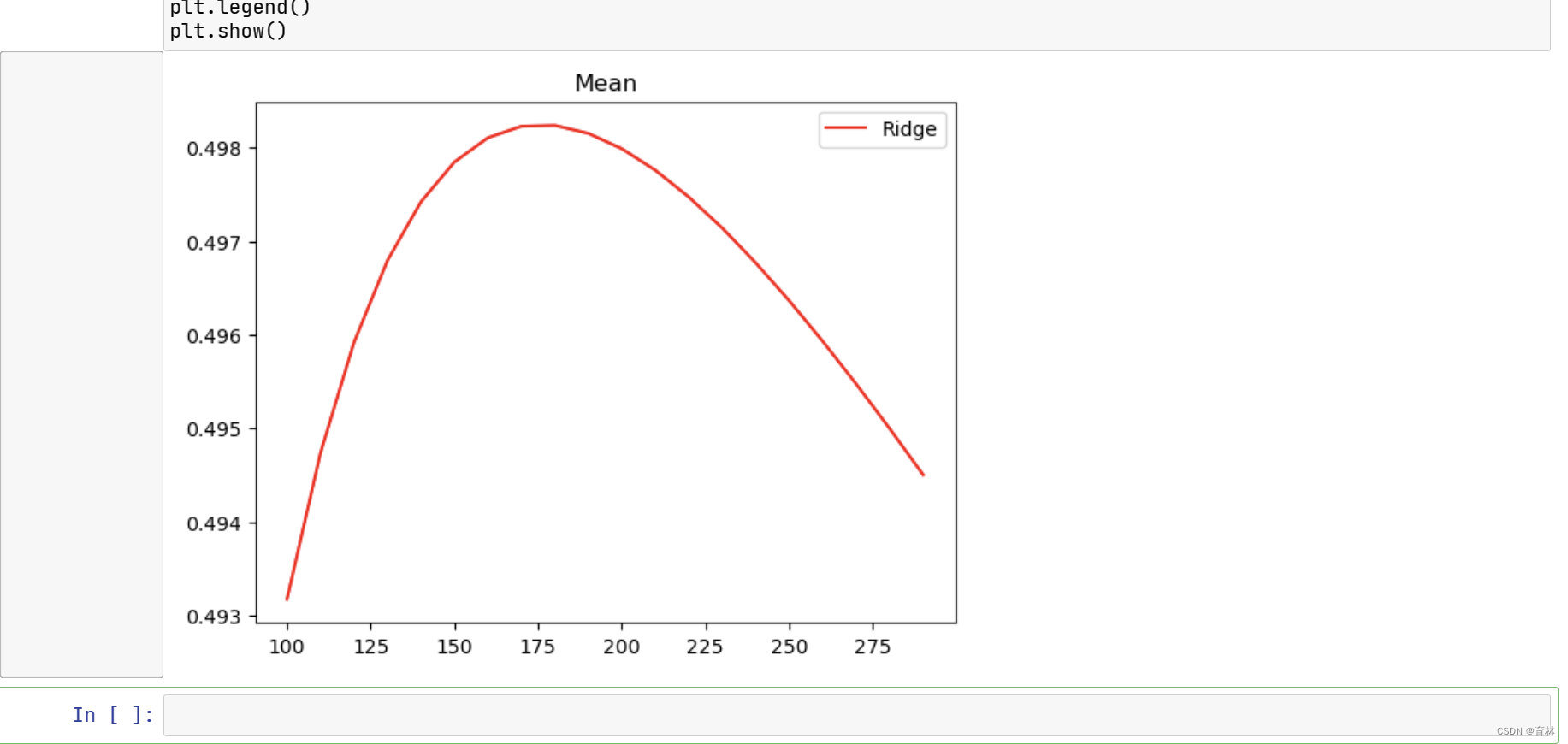
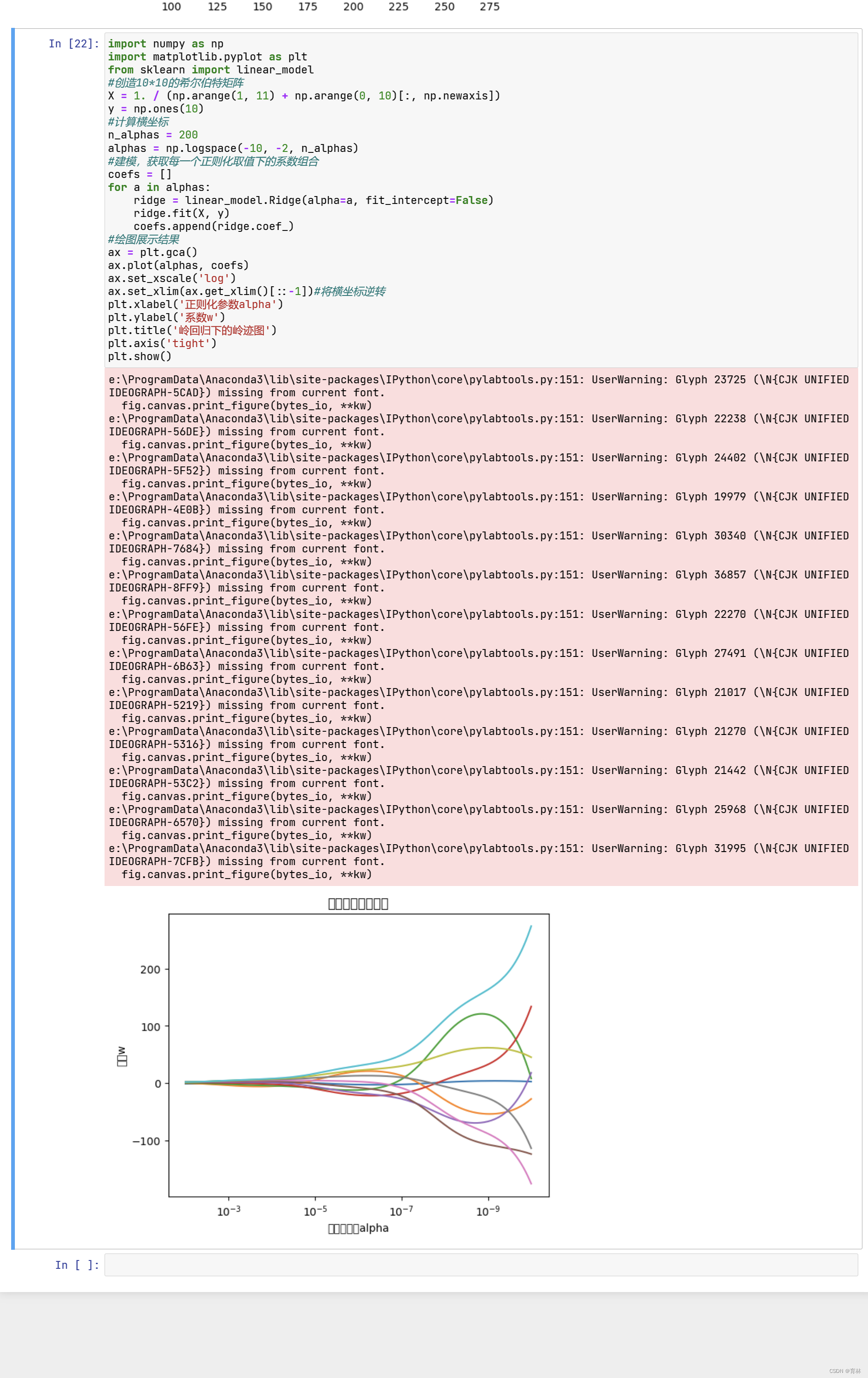
非常不建议大家使用岭迹图来作为寻找最佳参数的标准。
有这样的两个理由：

1. 岭迹图的很多细节，很难以解释。比如为什么多重共线性存在会使得线与线之间有很多交点？当 很大了之后看上去所有的系数都很接近于0，难道不是那时候线之间的交点最多吗？
2. 岭迹图的评判标准，非常模糊。哪里才是最佳的喇叭口？哪里才是所谓的系数开始变得”平稳“的时候？一千个读者一千个哈姆雷特的画像？未免也太不严谨了。
   
   
   

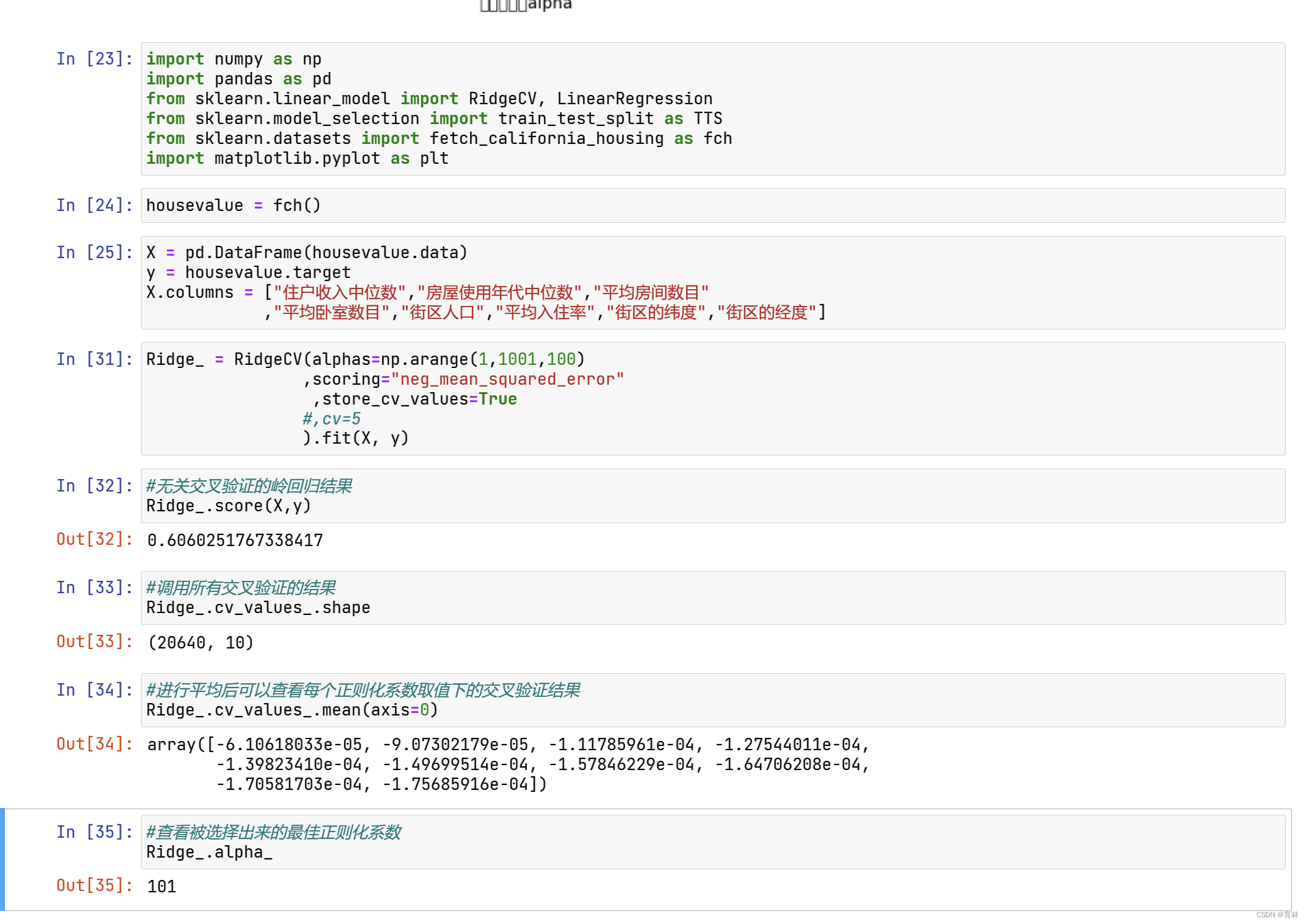
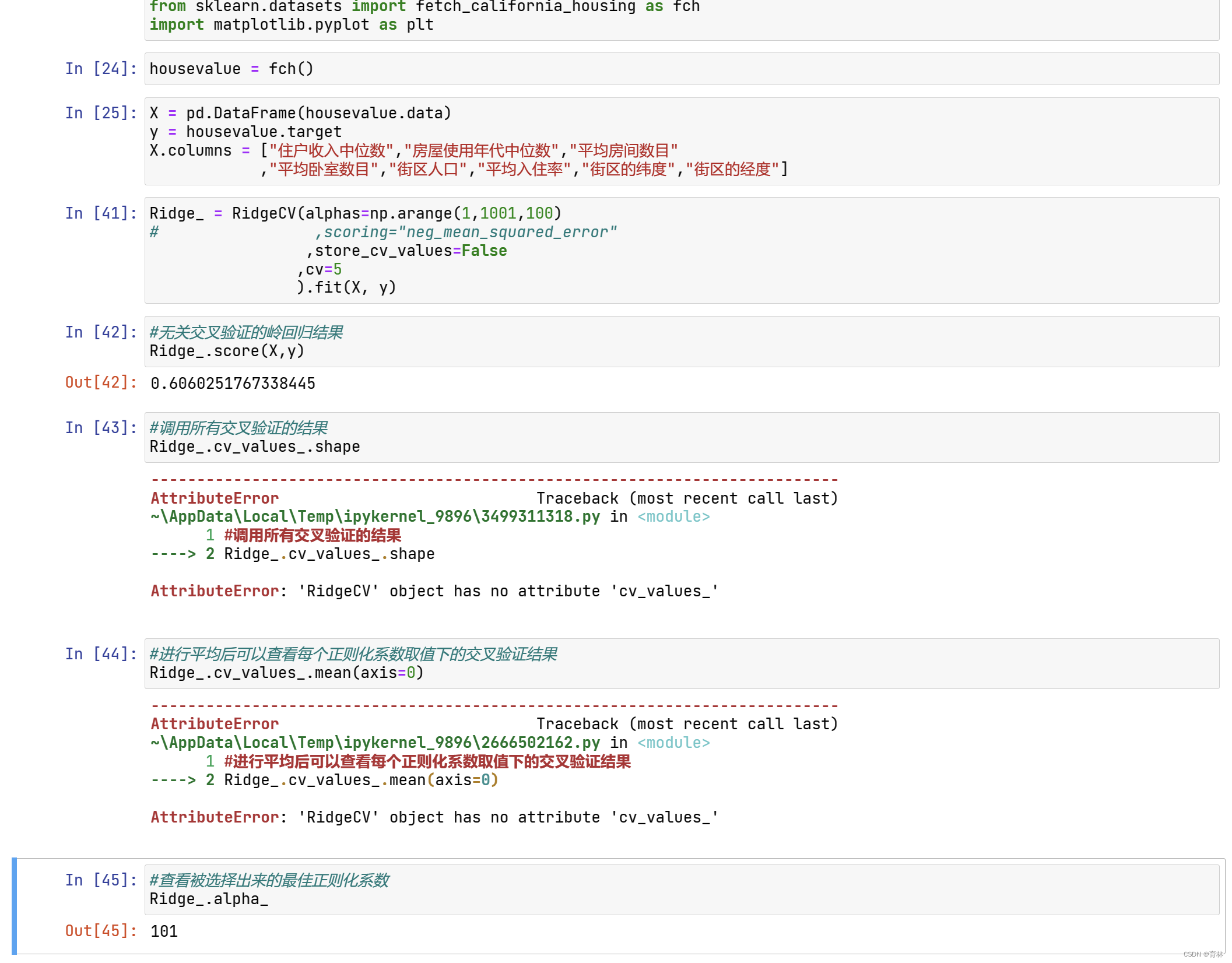
四、Lasso

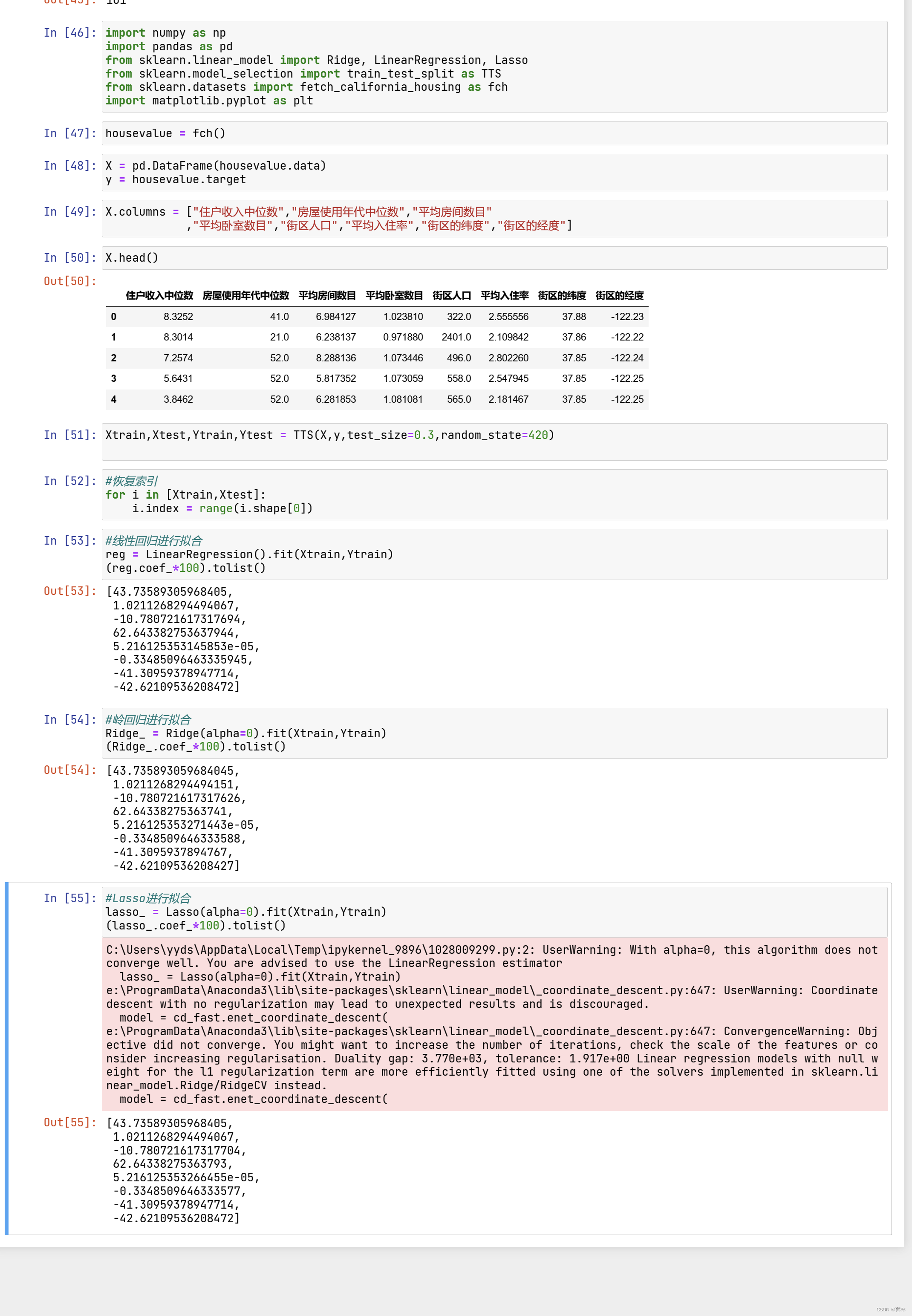
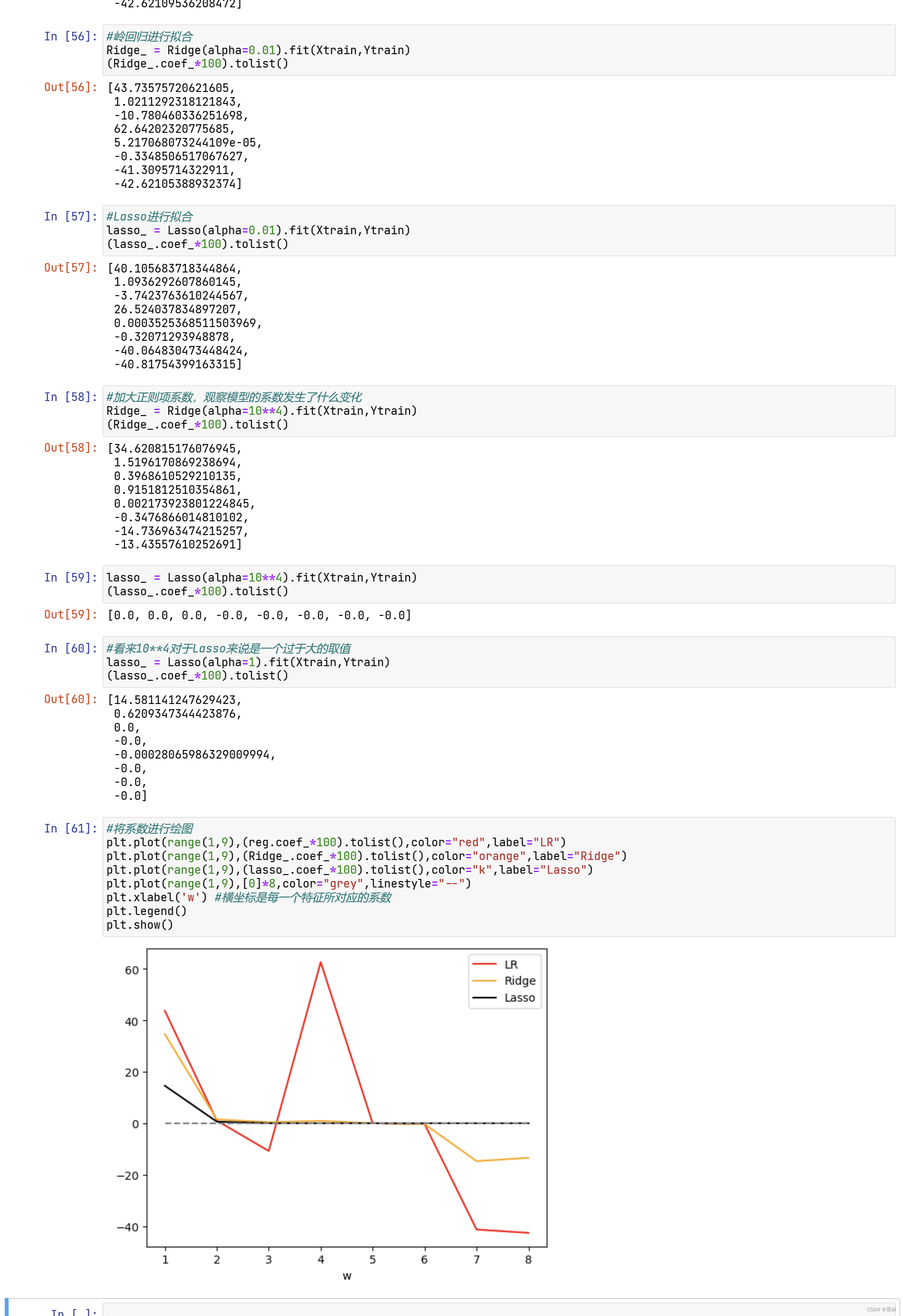
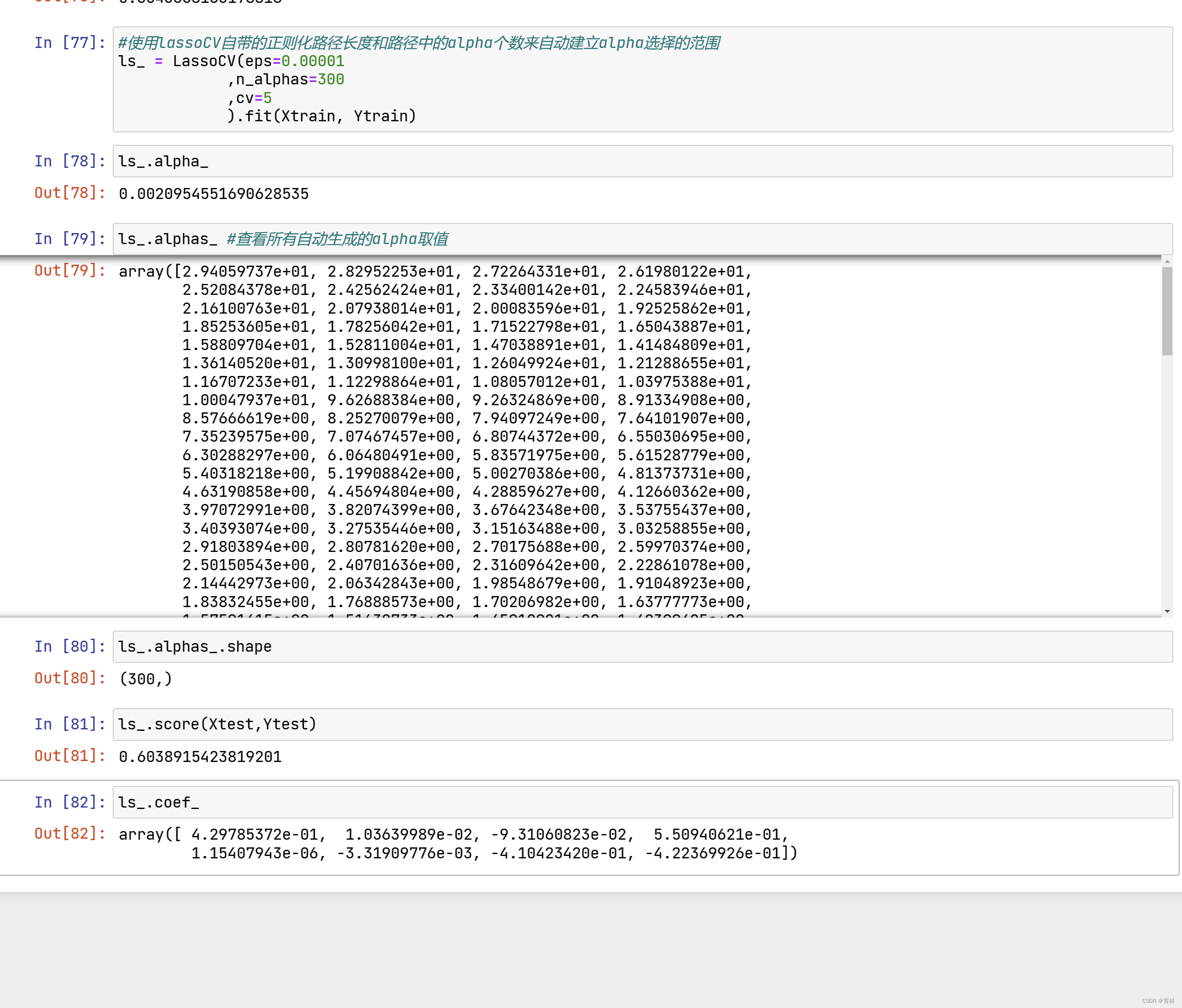
选取最佳的正则化参数取值

class sklearn.linear_model.LassoCV (eps=0.001, n_alphas=100, alphas=None, fit_intercept=True,normalize=False, precompute=’auto’, max_iter=1000, tol=0.0001, copy_X=True, cv=’warn’, verbose=False,n_jobs=None, positive=False, random_state=None, selection=’cyclic’)
使用交叉验证的Lasso类的参数看起来与岭回归略有不同，这是由于Lasso对于alpha的取值更加敏感的性质决定的。之前提到过，由于Lasso对正则化系数的变动过于敏感，因此我们往往让 在很小的空间中变动。这个小空间小到超乎人们的想象（不是0.01到0.02之间这样的空间，这个空间对lasso而言还是太大了），因此我们设定了一个重要概念“正则化路径”，用来设定正则化系数的变动。

总结