一、并查集
并查集(Disioint Set):一种非常精巧而实用的数据结构·用于处理不相交集合的合并问题。
用于处理不相交集合的合并问题。
经典应用:
连通子图。
最小生成树Kruskal算法。
最近公共祖先。
二、应用场景
有n个人,他们属于不同的帮派。
已知这些人的关系,例如1号、2号是朋友,1号、3号也是朋友,那么他们都属于一个帮派。
问有多少帮派,每人属于哪个帮派。
有n个人一起吃饭,有些人互相认识认识的人想坐在一起,而不想跟陌生人坐。
例如A认识B,B认识C,那么A、B、C会坐在一张桌子上。
给出认识的人,问需要多少张桌子。

用并查集可以很简洁地表示这个关系。
三、并查集的操作
初始化
定义s[ ]是以结点i为元素的并查集。
初始化:令s[i]=i (联想:某人的号码是i,他属于帮派s[i])。
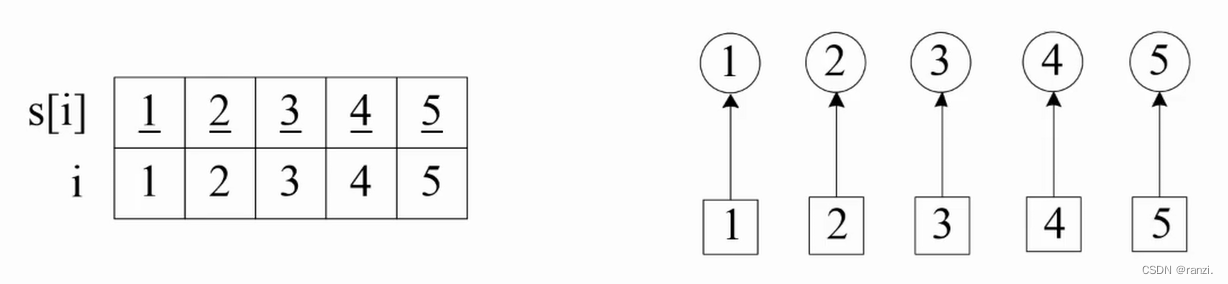
代码:

合并
加入第一个朋友关系(1,2):
在并查集s中,把结点1合并到结点2,也就是把结点1的集1改成结点2的集2。
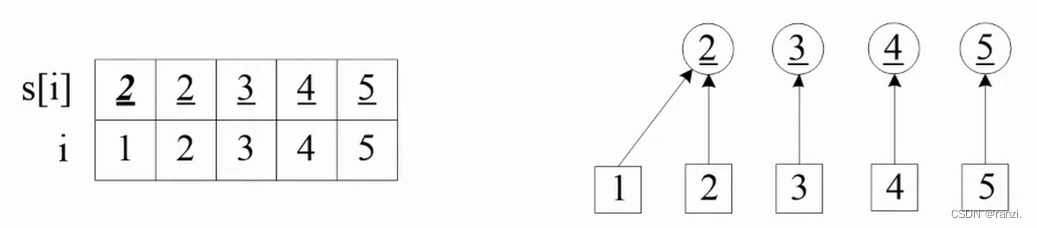
加入第二个朋友关系(1,3):
查找结点1的集,是2,递归查找元素2的集是2;把元素2的集2合并到结点3的集3。此时,结点1、2、3都属于一个集。
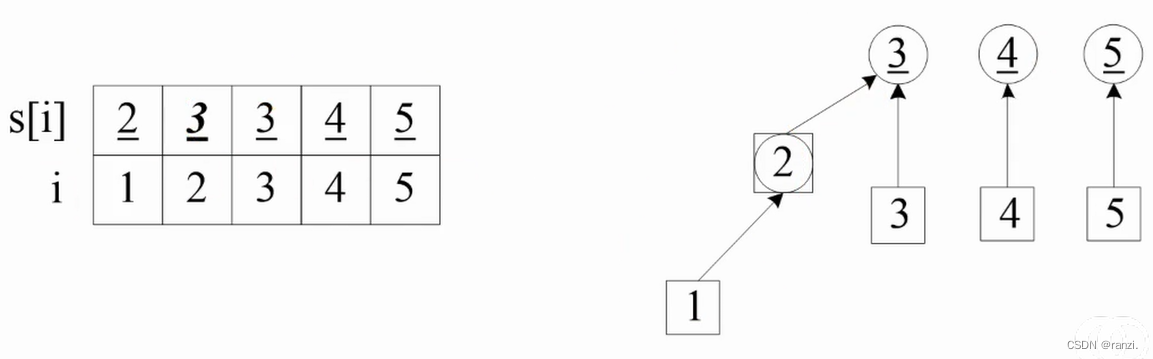
加入第三个朋友关系(2,4):
查找结点1的集,是2,递归查找元素2的集是2;把元素2的集2合并到结点3的集3。此时,结点1、2、3都属于一个集。
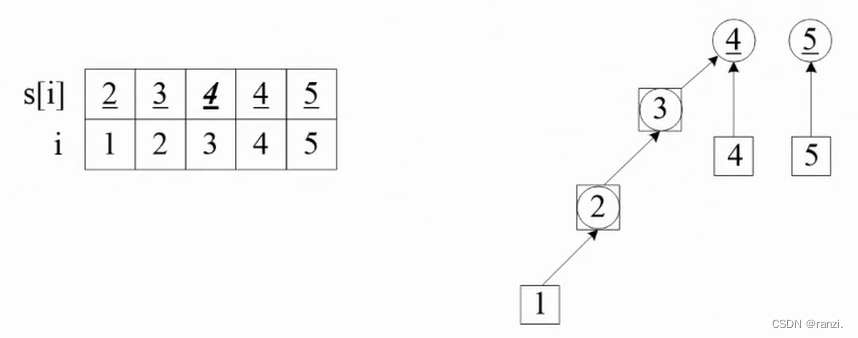
代码:
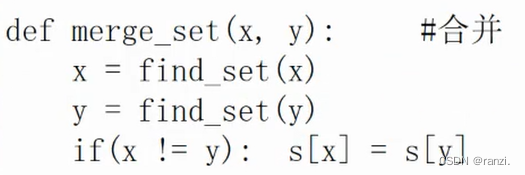
查找
查找元素的集,是一个递归的过程,直到元素的值和它的集相等,就找到了根结点的
集。
代码:

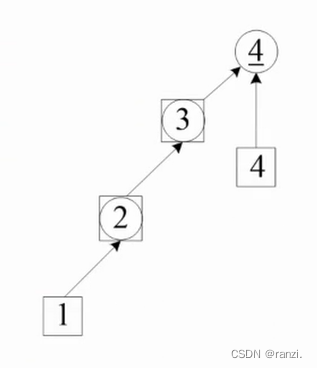
这棵搜索树,可能很细长,复杂度O(n),变成了一个链表,出现了树的“退化”现象。
总结
代码:

四、有多少个集(帮派) ?
如果s[i] = i,这就是一个根结点,是它所在的集的代表(帮主)。统计根结点的数量,就是集的数量。
复杂度:
查找find_set()、合并merge_set()的搜索深度是树的长度,复杂度都是O(n)。性能较差,不是高级数据结构应有的复杂度。
复杂度的优化:
能优化吗? 能 目标:优化之后,复杂度≈O(1)。
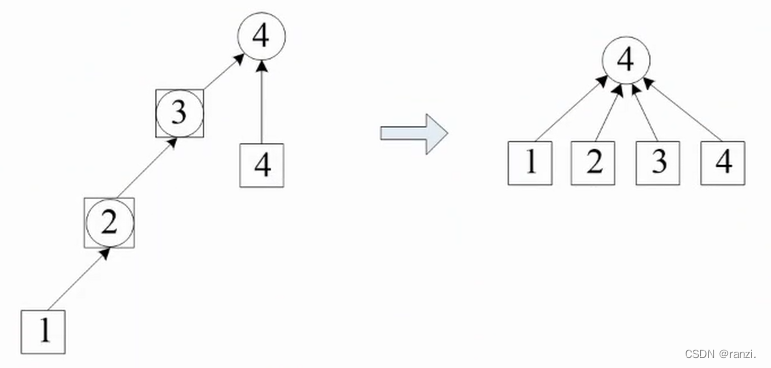
查询的优化(路径压缩):
查询程序find_set():沿着搜索路径找到根结点,这条路径可能很长。
优化:沿路径返回时,顺便把i所属的集改成根结点。下次再搜,复杂度是O(1)。
代码:

优化前后代码对比:

路径压缩总结:
路径压缩通过递归实现。
整个搜索路径上的元素,在递归过程中,从元素i到根结点的所有元素,它们所属的集都被改为根结点。
路径压缩不仅优化了下次查询,而且也优化了合并,因为合并时也用到了查询。
五、蓝桥杯真题(1135号)



六、蓝桥杯真题(1135号)

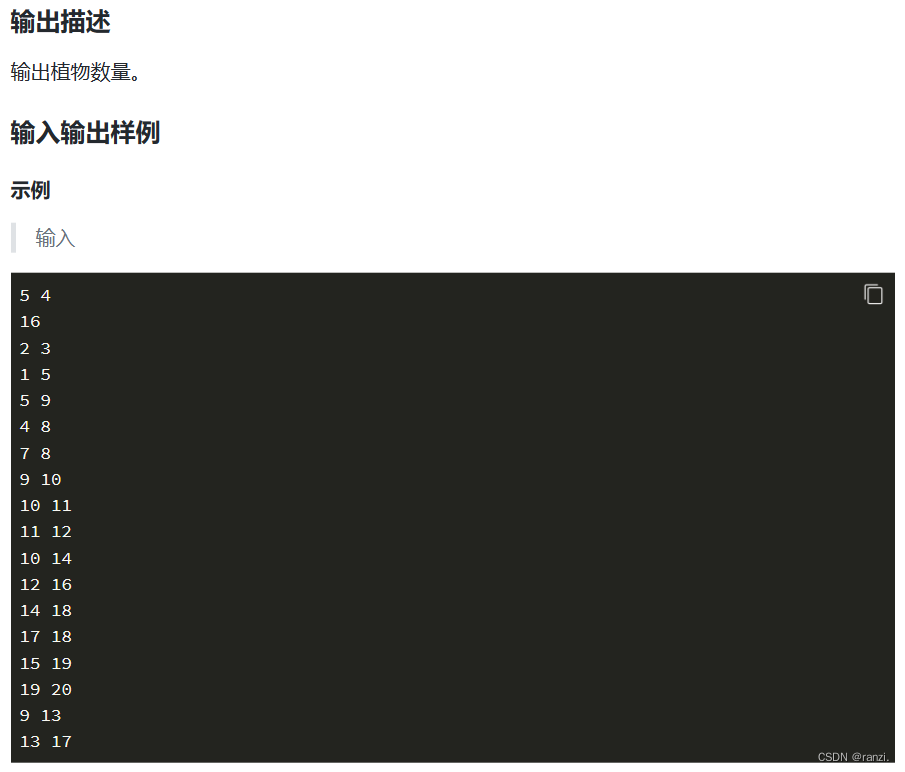
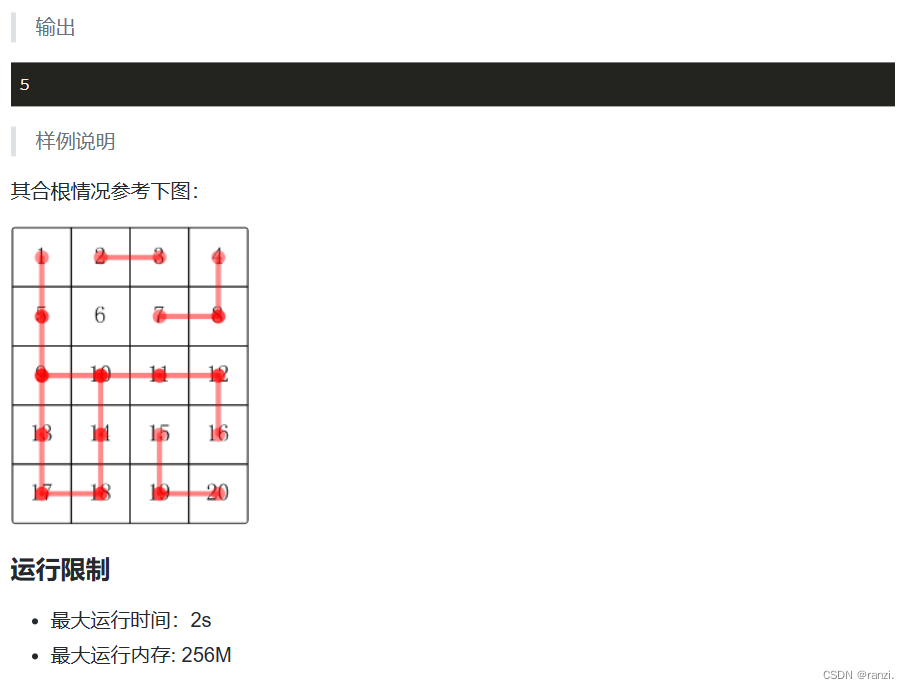

七、蓝桥杯真题(185号)


1.暴力法
1≤N≤100000
每读入一个新的数,就检查前面是否出现过,每一次需要检查前面所有的数。共有n个数,每个数检查O(n)次,总复杂度O(n^3),超时。
暴力法1

暴力法2

2.查重,hash或set()
改进,用hash。定义vis[]数组,vis[i]表示数字i是否已经出现过。这样就不用检查前面所有的数了,基本上可以在O(1)的时间内定位到。
或:直接用set判断是否重复,也是O(1)。

3.改进:记忆法
本题特殊要求:“如果新的Ai仍在之前出现过,小明会持续给Ai加1,直到Ai,没有在A1~Ai-1中出现过。”这导致在某些情况下,仍然需要大量的检查。
以5个6为例:A[ ]={6,6,6,6,6}。
第一次读A[1]=6,设置vis[6]=1。
第二次读A[2]=6,先查到vis[6]=1,则把A[2]加1,变为a[2]=7;再查vis[7]=0,设置vis[7]=1。检查了2次。
第三次读A[3]=6,先查到vis[6]=1,则把A[3]加1得A[3]=7; 再查到vis[7]=1,再把A[3]加1得A[3]=8,设置vis[8]=1; 最后查vis[8]=0,设置vis[8]=1。检查了3次。
......
每次读一个数,仍需检查O(n)次,总复杂度O(n^2)。
本题用Hash,在特殊情况下仍然需要大量的检查。
问题出在“持续给Ai加1,直到Ai没有在A1~Ai-1中出现过”。
也就是说,问题出在那些相同的数字上。当处理一个新的Ai时,需要检查所有与它相同的数字。
如果把这些相同的数字看成一个集合,就能用并查集处理。
用并查集s[i]表示访问到i这个数时应该将它换成的数字。
以A[ ]={6,6,6,6,6}为例。初始化set[i]=i。

图(1)读第一个数A[0]= 6。6的集set[6]= 6。紧接着更新set[6] = set[7] = 7,作用是后面再读到某个A[k]=6时,可以直接赋值A[k] = set[6]= 7。
图(2)读第二个数A[1]=6。6的集set[6]=7,更新A[1]= 7。紧接着更新set[7]= set[8]= 8。如果后面再读到A[k]= 6或7时,可以直接赋值A[k]= set[6]= 8或者A[k]= set[7]=8。
只用到并查集的查询,没用到合并。
必须是“路径压缩”优化的,才能加快查询速度。没有路径压缩的并查集,仍然超时。
复杂度O(n)