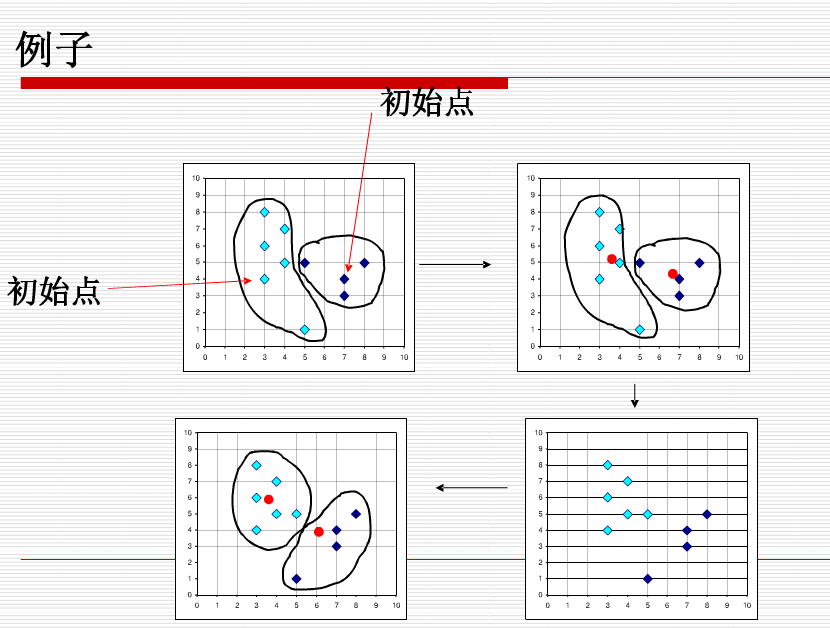
k-means算法
k-means算法,也被称为k-平均或k-均值,是一种得到最广泛应用的聚类算法。

算法首先随机选择k个对象,每个对象初始地代表了一个簇的平均值或中心。对剩余的每个对象根据其与各个簇中心的距离,将它赋给最近的簇。然后重新计算每个簇的平均值。这个过程不断重复直到准则函数收敛。
准则函数试图使生成的结果簇尽可能地紧凑和独立。
算法步骤
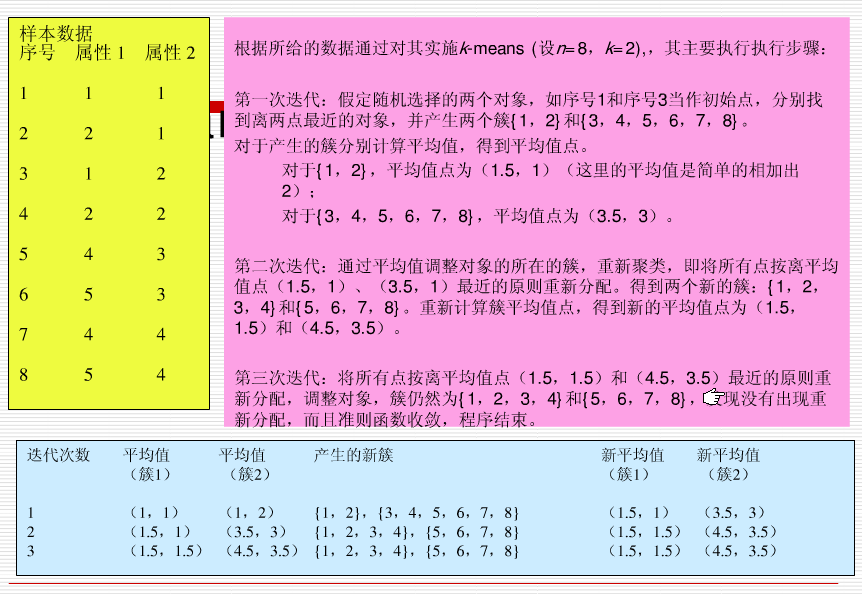
(1) 首先我们选择一些类/组,并随机初始化它们各自的中心点。中心点是与每个数据点向量长度相同的位置。这需要我们提前预知类的数量(即中心点的数量)。
(2) 计算每个数据点到中心点的距离,数据点距离哪个中心点最近就划分到哪一类中。
(3) 计算每一类中中心点作为新的中心点。
(4) 重复以上步骤,直到每一类中心在每次迭代后变化不大为止。也可以多次随机初始化中心点,然后选择运行结果最好的一个。

算法优点
(1)速度快;
(2)计算简便 ;
算法缺点
(1)我们必须提前知道数据有多少类/组;
(2)K-Medians是K-Means的一种变体,是用数据集的中位数而不是均值来计算数据的中心点。;
(3)K-Means对于“噪声”和“孤立点数据”等异常值是敏感的,K-Medians的优势是使用中位数来计算中心点不受异常值的影响;缺点是计算中位数时需要对数据集中的数据进行排序,速度相对于K-Means较慢。