摘要

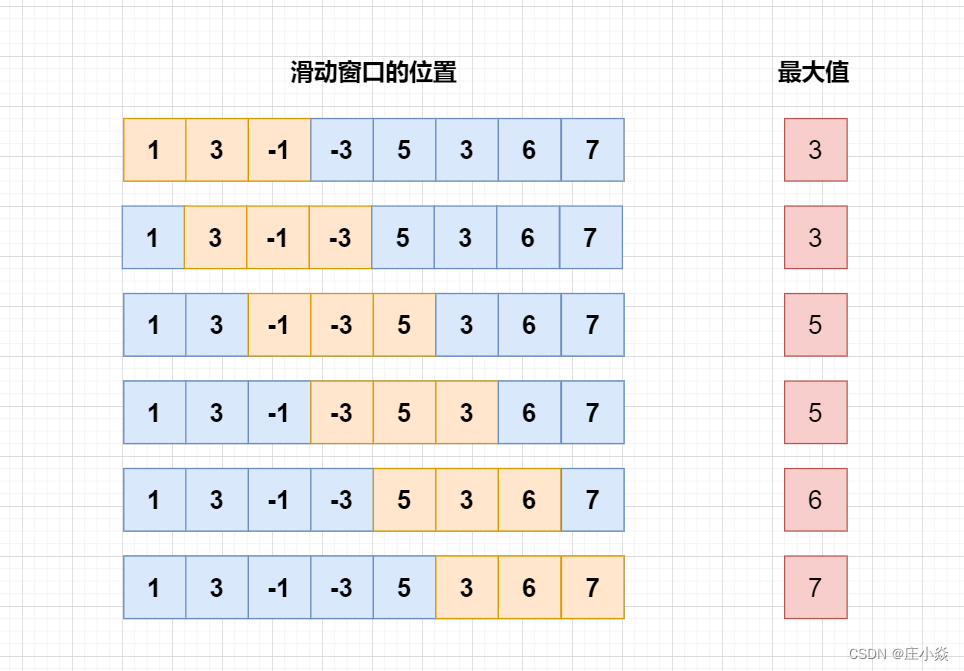
剑指 Offer 59 - I. 滑动窗口的最大值

一、大顶堆求解

对于每个滑动窗口，我们可以使用 O(k) 的时间遍历其中的每一个元素，找出其中的最大值。对于长度为n的数组 nums而言，窗口的数量为 n−k+1，因此该算法的时间复杂度为 O((n−k+1)k)=O(nk)，会超出时间限制，因此我们需要进行一些优化。

    public int[] maxSlidingWindow1(int[] nums, int k) {
        PriorityQueue<Integer> queue=new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2.compareTo(o1);
            }
        });
        int[] result=new int[nums.length-(k-1)];
        int x=0;
        // 将数据放置到queue中
        int index=0;
        while (index<nums.length){
            while (index<nums.length&&(queue.isEmpty()||queue.size()!=k)){
                queue.add(nums[index++]);
            }
            result[x++]=queue.peek();
            queue.remove(nums[index-k]);
        }
        return result;
    }

复杂度分析

时间复杂度：O(nlong(n)) ，n次遍历，log(n)每一次大顶堆的找到的最大值

空间复杂度：O(n) 存储结果数据量。

二、双端队列

我们可以想到，对于两个相邻（只差了一个位置）的滑动窗口，它们共用着 k−1个元素，而只有 1 个元素是变化的。我们可以根据这个特点进行优化。

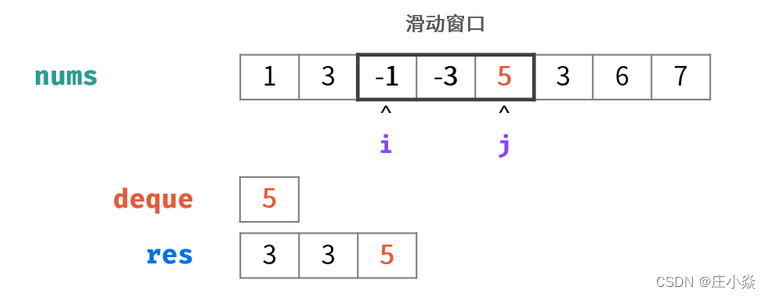
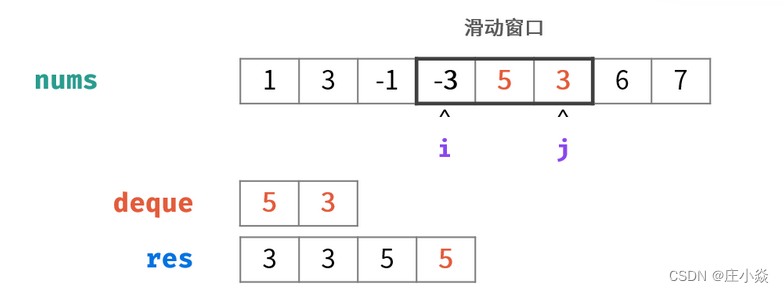
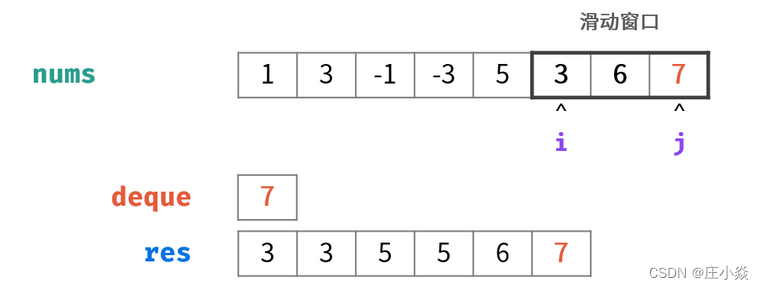
窗口对应的数据结构为双端队列 ，本题使用单调队列即可解决以上问题。遍历数组时，每轮保证单调队列 deque：

deque 内仅包含窗口内的元素⇒ 每轮窗口滑动移除了元素 nums[i−1] ，需将 deque内的对应元素一起删除。
deque内的元素非严格递减⇒ 每轮窗口滑动添加了元素 nums[j+1]，需将 deque内所有 <nums[j+1]的元素删除。

算法流程：

初始化：双端队列deque，结果列表res ，数组长度 n；
滑动窗口：左边界范围 i∈[1−k,n−k] ，右边界范围 j∈[0,n−1]；
若 i>0且队首元素deque[0]== 被删除元素 nums[i−1] ：则队首元素出队；
删除deque内所有<nums[j]的元素，以保持 deque递减；
将 nums[j]添加至deque尾部；
若已形成窗口（即 i≥0）：将窗口最大值（即队首元素 deque[0]）添加至列表 resres ；
返回值：返回结果列表res；

    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums.length == 0 || k == 0) {
            return new int[0];
        }
        // 构建一个双端队列
        Deque<Integer> deque = new LinkedList<>();
        // 表示最后的存储结果的大小
        int[] res = new int[nums.length - k + 1];
        for (int j = 0, i = 1 - k; j < nums.length; i++, j++) {
            // 删除 deque 中对应的 nums[i-1]
            if (i > 0 && deque.peekFirst() == nums[i - 1]) {
                deque.removeFirst();
            }
            // 保持 deque 递减
            while (!deque.isEmpty() && deque.peekLast() < nums[j]) {
                deque.removeLast();
            }
            deque.addLast(nums[j]);
            // 记录窗口最大值
            if (i >= 0) {
                res[i] = deque.peekFirst();
            }
        }
        return res;
    }

public int[] maxSlidingWindow3(int[] nums, int k) {
        if (nums.length == 0 || k == 0) {
            return new int[0];
        }
        // 头部是最大的值 并保持单调递减。
        Deque<Integer> deque = new LinkedList<>();
        int[] res = new int[nums.length - k + 1];
        // 未形成窗口
        for (int i = 0; i < k; i++) {
            while (!deque.isEmpty() && deque.peekLast() < nums[i]) {
                deque.removeLast();
            }
            deque.addLast(nums[i]);
        }
        res[0] = deque.peekFirst();
        // 形成窗口后
        for (int i = k; i < nums.length; i++) {
            if (deque.peekFirst() == nums[i - k]) {
                deque.removeFirst();
            }
            while (!deque.isEmpty() && deque.peekLast() < nums[i]) {
                deque.removeLast();
            }
            deque.addLast(nums[i]);
            res[i - k + 1] = deque.peekFirst();
        }
        return res;
    }

复杂度分析：