二叉树的前序遍历，非递归迭代实现

题目链接
思路：
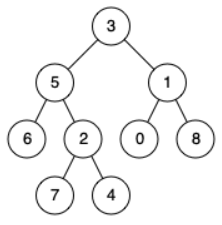
将任何一颗树分成两个部分，一部分是左路节点（3、5、6），另一部分左路节点的若干个右子树（2、7、4、1、0、8）。
先将左路结点入栈，因为是前序遍历，入一个结点，就访问一个结点，然后从栈顶开始判断这个结点是否有右子树，没有右子树就只将其从栈中pop掉，
有右子树的话先把这个结点记录一下，然后从栈中pop掉，然后再去这个结点的右子树找，把这个结点的右子树也划分为左路结点和左路结点的右子树，循环前面的过程。
在这里插入图片描述
代码：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> v;//存二叉树的数据
        stack<TreeNode*> s;//遍历二叉树的容器

        TreeNode*cur=root;
        while(cur||!s.empty())//当栈不为空或者cur不为空时循环才会继续
        //有可能一上来s是空的，此时就要拿cur来判断
        {
            //开始访问一棵树
            while(cur)
            {
                v.push_back(cur->val);//前序遍历就要先存数据
                //把左路结点依次入栈
                s.push(cur);
                cur=cur->left;
            }

            //第一次栈顶是最左下方的结点，接下来访问左路结点的右子树
            cur=s.top()->right;
            //这个结点已经用v记录了，出栈
            s.pop();
        }
        return v;
    }
};

二叉树的中序遍历，非递归迭代实现

题目链接
思路：
和前序遍历的思路差不多，就是要先把左路结点入栈，然后再访问根结点，然后再去根的右子树，把访问过的根出栈。再把右子树的左路结点入栈…，就这样循环往复，直到栈里没有元素为止。
代码：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> s;

        TreeNode*cur=root;
        while(cur||!s.empty())
        {
            
            while(cur)
            {
                s.push(cur);
                cur=cur->left;
            }

            v.push_back(s.top()->val);

            cur=s.top()->right;
            s.pop();

        }

        return v;
    }
};

二叉树的后序遍历，非递归迭代实现

题目链接
在这里插入图片描述
思路：

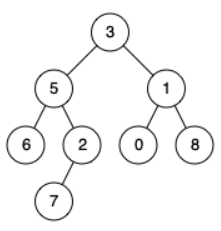
大思路和前序中序的一样，就是将一棵树的左路结点(3、5、6)先入栈，因为是后序遍历，要后访问根。
与前序和中序不一样的是：要在push_back到v的时候，s即将被pop的之前，记录一下这个结点的地址before_root，方便确定是否一个根的右子树是否已经被访问了，如果被访问了，那么才可以访问根自己。
模拟一下过程：
从小问题开始转化，从此时的栈顶6开始，如果6的右子树为空，那么才可以访问6。然后出栈。接着栈顶此时是5，看5的右子树不为空，看看before_root上一个访问的地址是谁，很显然上一次访问的是6，5的右子树没有访问，那么把右子树的左路再入栈。再划分成一个个子问题。
如果before_root记录的时候2的地址，好，那么说明5的右子树已经被访问，这时才能访问5自己。
代码：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> s;

        TreeNode*cur=root;
        TreeNode*before_root=nullptr;//记录前一个结点的变量
        while(cur||!s.empty())
        {
            
            while(cur)
            {
                
                s.push(cur);
                cur=cur->left;
            }

            
            if(s.top()->right==nullptr||before_root==s.top()->right)
            //右子树为空或者右子树已经被访问过了才能访问自己
            {
                v.push_back(s.top()->val);
                before_root=s.top();//记录一下这个节点的地址
                s.pop();
            }
            else//右子树不为空且没有被访问，要去右子树中将左路结点入栈
            {
                cur=s.top()->right;
            }

        }

        return v;
    }
};