【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波

文章目录

【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波
- 1. 前言
- 2. 符号说明
- 3. 三种滤波
- - 3.1 全通滤波
  - 3.2 低通滤波
  - - 3.2.1 平滑信号分析
    - 3.2.2 广义拉普拉斯平滑滤波器
  - 3.3 高通滤波
- 4. 总结

1. 前言

GCN：图卷积神经网络。它不同于只用于网格结构数据的传统模型：LSTM，CNN等。是一种处理广义拓扑图结构的数据，深入挖掘其特征和规律的工具。（社交网络，通信网络，蛋白质分子等），这里也捎带补充一下广义拓扑图的概念：将实体抽象成与大小形状无关的点，点之间连接成线形成的图。GCN的发展史如下：

2005年，Marco Gori等人发表了论文，首次提出了GNN的概念，在此之前，处理图数据的方法是在数据的预处理阶段将图转换为用一组向量表示。这种处理方法会丢失很多的结构信息，得到的结果会严重依赖于对图的预处理，GNN的提出能够将学习过程直接架构在图数据之上。
2009年，进一步的阐述了图神经网络，提出了一种监督的方法来训练GNN，但是，早期的研究都是以迭代的方式，通过RNN传播邻居消息，直到达到稳定的固定状态来学习节点的表示。这种计算消耗极大。
2012年，CNN在CV上取得了很好的成绩，于是开始将卷积应用在GNN中。
2013年，Bruna等人提出了GCN，这时候的GCN是基于频域卷积的。后来又有很多人对它进行改进，拓展，但是频域卷积在计算时需要同时处理整个图，并且需要承担矩阵分解时很高的时间复杂度。
2016年，Kipf等人将频域卷积的定义简化，使图卷积操作能够在空域进行，极大提高了图卷积模型的计算效率，同时，由于卷积滤波的高效性，GCN模型在很多图数据相关任务上取得了很好的成绩。
之后的近几年里，想频域卷积提出的那时候一样，更多的基于空域GCN的变体被开发出来。这类方法都统称为GNN。各种GNN模型，大大加强了对各类图数据的适应性。
2018年，该领域不约而同地同时发表3篇综述论文。
2019年，各大顶级学术会议上GNN占据很大份额。

将来GNN的趋势会只增不减，只要我们好好利用它，相信能够很好的收获。

2. 符号说明

图数据可以表示为具有节点集 V 和边集 E 的图G =（V，E），其中点集V，n=|V|是节点数。这些节点是由该特征来描述的。矩阵X∈R $^{n×f}$ ，其中 f 为节点特征的维数。G的图结构可以用邻接矩阵A∈R $^{n×n}$ 来描述，其中，如果节点 i 和节点 j 之间有一条边，则为 $A_{ij}$ = 1，否则为0。对角度矩阵记为 D=diag（d1，···，dn），其中 $d_i =\sum_j A_{ij}$ 。我们使用 $\tilde A=A+I$ 来表示添加了自循环的邻接矩阵和 $\tilde D=D+I$ 。传统的图拉普拉斯矩阵为： $\tilde D - \tilde A$ 。然后归一化的邻接矩阵是 $\hat{\tilde{A}} = \tilde D ^{−1/2}\tilde A \tilde D ^{−1/2}$ 。相应地， $\tilde L = I − \hat{\tilde{A}}$ 是归一化对称正半定图拉普拉斯矩阵。

3. 三种滤波

$I$ 、 $\hat {\tilde{A}}$ 、 $\tilde L$ ，分别对应有全通、低通、高通滤波的算子（图卷积核/滤波器）**

3.1 全通滤波

公式为： $Z_{all} = IX$
全通滤波也即所有的信号都可以通过，即不对图信号做处理。

3.2 低通滤波

公式为： $Z_{low} = \hat {\tilde{A}} X$
低通滤波本质上就是为了使图上的特征变得光滑。下面进行解释：

图学习的基本假设是，图上相邻的节点应该是相似的，因此在图域上的节点特征应该是平滑的。本节首先解释了平滑的意思；然后给出了广义拉普拉斯平滑滤波器的定义，并证明了它是一个平滑算子；最后回答了如何设计一个最优的拉普拉斯平滑滤波器。

3.2.1 平滑信号分析

从图信号处理的角度来解释平滑开始。以 $x\in R^n$ 作为图上的信号，节点 $i$ 的信号就是一个标量，也就是 $x_i$ 。滤波矩阵为 $H$ ，为了测量图信号 $x$ 的平滑度，可以计算出图的拉普拉斯算子 $L$ ( $L = D - A$ )和 $x$ 上的瑞利商：

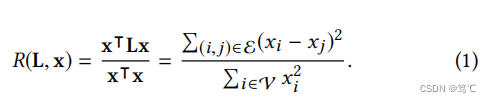
这个商实际上是 $x$ 的标准化方差分数。如上所述，平滑信号应该在相邻节点上分配相似的值。因此，瑞利商越低，则图上的信号越平滑。

考虑图拉普拉斯 $L=UΛU^{−1}$ 的特征分解，其中 $\in R^{n\times n}$ 包含特征向量， $Λ = d ia g (λ 1 ， λ 2 ， \cdot\cdot\cdot ， λn)$ 是特征值的对角矩阵。随后可以给出了特征向量 $u_i \in U$ 的光滑性:

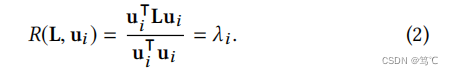
上式表示较平滑的特征向量与较小的特征值相关联，即频率较低。因此，基于等式基于 $L$ 分解信号 $x$ 基于公式（1）和（2）:

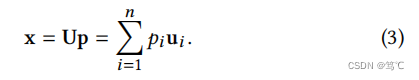
其中 $p_i$ 是特征向量 $u_i$ 的系数。那么 $x$ 的平滑度就变成了：

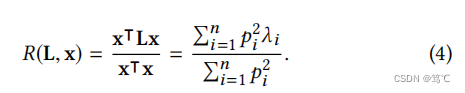
因此，为了获得更平滑的信号，滤波器的目标是：在保留低频分量的同时，滤掉高频分量。由于其高计算效率和令人信服的性能，拉普拉斯平滑滤波器经常被用于这一目的（保留低频分量的同时，滤掉高频分量）。

3.2.2 广义拉普拉斯平滑滤波器

广义拉普拉斯平滑滤波器定义为：

其中 $k$ 是实值的。采用 $H$ 作为滤波器矩阵，滤波后的信号 $\tilde{x}$ 被表示为:

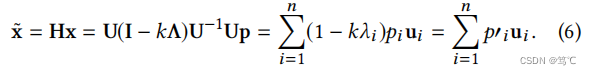
因此，为了实现低通滤波，频率响应函数 $1 - kλ$ 应该是一个递减和非负函数。因为需要使特征值 λ 越大，对应的 $p^{'} i$ 系数就越小，这样可以使得图上的瑞丽商变小，进而光滑，进而实现低通（频率低的特征通过，频率低也就意味着光滑）。
注意，该过滤器是不含有参数的。

3.3 高通滤波

公式为： $Z_{high} = \tilde L X$
说完低通滤波，高通滤波则与之相反。即不对这个函数进行限制。
此时，上述的公式（6）就变成了：
$\tilde x = Hx = UΛU^{-1}Up = \sum^{n}_{i=1} λ_i p_i u_i$
此时， $u_i$ 对应的图信号频率越高，其特征值 λ 越大，这样频率也就越大了，从而图上高频信号变多，进而实现了高通。