并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中。其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
并查集是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的合并及查询问题。常常在使用中以森林来表示。
并查集操作:(1)将两个集合合并;(2)询问两个元素是否在一个集合中。并查集可以在近乎O(1)的时间复杂度内支持这两种操作。
一、并查集基本原理
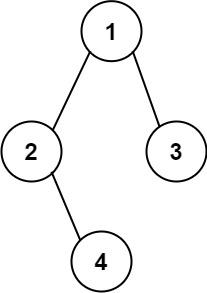
并查集的核心思想是用一棵树来表示一个集合。树根的编号就是整个集合的编号。有一个p数组,存储每个节点的父节点,p[x] = a表示节点x的父节点是节点a。
解决并查集问题需要解决如下几个子问题:
(1)如何让判断找到了树根(停止回溯):if(p[x] == x),表示树根的父节点用本身表示,除了树根之外,任何节点的父亲