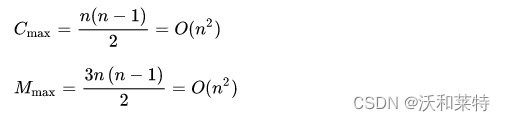前言

上一篇文章 PHP学习笔记（观隅反三）分享了数组的知识，这篇文章接着分享和数组相关的算法。

算法效率

算法效率分为两种：第一种是时间效率，第二种是空间效率。时间效率被称为时间复杂度，而空间效率被称作空间复杂度。时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间。

`冒泡排序`

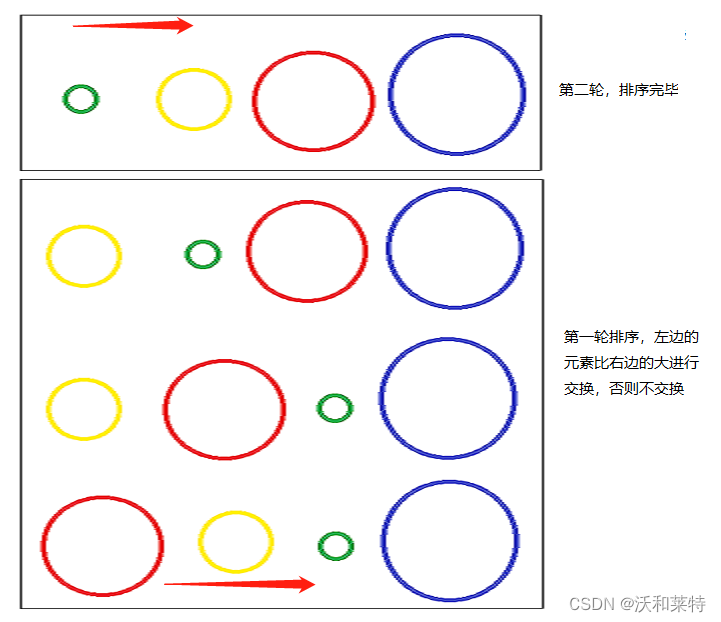
冒泡排序算法的原理如下：
比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

$arr1=array(1,2,4,3,5,0,8);
for($j=0;$j<count($arr1);$j++){
    for($i=0;$i<count($arr1)-1-$j;$i++){
        if($arr1[$i]>$arr1[$i+1]){
            $temp=$arr1[$i];
            $arr1[$i]=$arr1[$i+1];
            $arr1[$i+1]=$temp;
        }
    }   
}
echo '<pre>';
print_r($arr1);
//Array ( [0] => 0 [1] => 1 [2] => 2 [3] => 3 [4] => 4 [5] => 5 [6] => 8 )

时间复杂度

若文件的初始状态是正序的，一趟扫描即可完成排序。所需的关键字比较次数C和记录移动次数M均达到最小值：C_min=n-1 ; M_min=0 ；
所以，冒泡排序最好的时间复杂度为O(n) 。
若初始文件是反序的，需要进行 n-1 趟排序。每趟排序要进行 n-i 次关键字的比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值：

冒泡排序的最坏时间复杂度为 O(n²)。
综上，因此冒泡排序总的平均时间复杂度为 O(n²)。 [1]

稳定性

冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较，交换也发生在这两个元素之间。所以，如果两个元素相等，是不会再交换的；如果两个相等的元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，所以相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。

`选择排序`

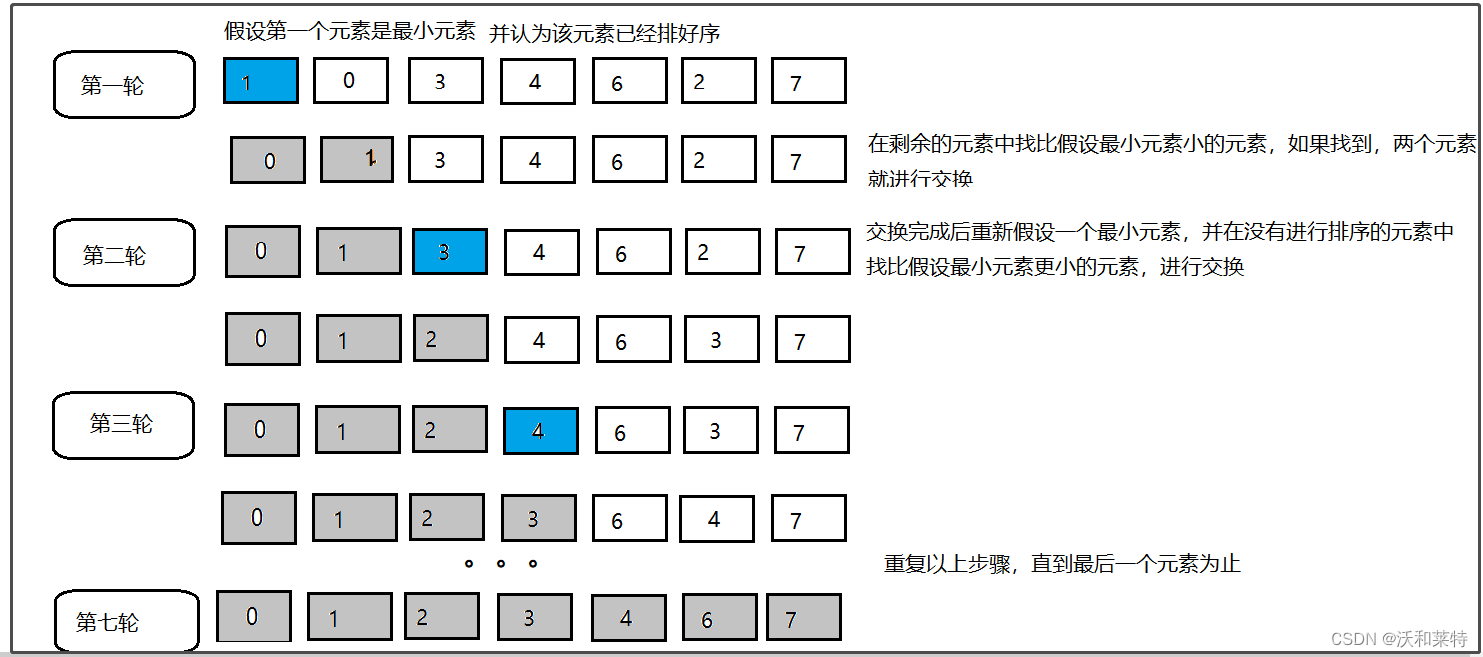
选择排序原理如下：
第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

$arr2=array(1,0,3,4,6,2,7);
for($i=0;$i<count($arr2);$i++){
    // 选定一个元素下标，假定其为最小元素下标，将其存储在变量$min中
    $min=$i;
    for($j=$i+1;$j<count($arr2);$j++){
        if($arr2[$j]<$arr2[$min]){
            $min=$j;
        }
    }
    // 如果选定的最小值不等于实际最小值，就进行交换
    if($min !=$i){
        $temp =$arr2[$i];
        $arr2[$i]=$arr2[$min];
        $arr2[$min]=$temp;
    }
}
print_r($arr2);
//Array ( [0] => 0 [1] => 1 [2] => 2 [3] => 3 [4] => 4 [5] => 6 [6] => 7 )

时间复杂度

选择排序的交换操作介于0 和 (n - 1)次之间。选择排序的比较操作为n (n - 1） / 2次之间。选择排序的赋值操作介于 0 和 3 (n - 1）次之间。比较次数O(n^2），比较次数与关键字的初始状态无关，总的比较次数N=(n-1）+(n-2）+…+1=n*(n-1）/2。交换次数O(n），最好情况是，已经有序，交换0次；最坏情况交换n-1次，逆序交换n/2次。交换次数比冒泡排序少多了，由于交换所需CPU时间比比较所需的CPU时间多，n值较小时，选择排序比冒泡排序快。

稳定性

在一趟选择，如果一个元素比当前元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。因此选择排序是一个不稳定的排序算法。

`插入排序`

插入排序:
通常称之为直接插入排序，当进行少量数据的排序中，还可以使用插入排序的方法，插入排序的方法是将一个数据插入到已经排好序的有序数据中，以此得到一个新的个数加一的数组，该方法比较稳定。

$arr3=array(1,0,3,4,6,2,7);
for($i=1,$len=count($arr3);$i<$len;$i++){
    // 选出要插入元素
    $temp = $arr3[$i];
    //选出有序数列，将待插入元素和有序数列进行比较，若前者比后者小，就将待插入元素插入到指定位置，待插入元素后的原有序数列往后移，补上待插入元素的空位
    for($j=$i-1;$j>=0;$j--){
        if($arr3[$j]>$temp){
            $arr3[$j+1]=$arr3[$j];
            $arr3[$j]=$temp;
        }else{
            // 如果当前需要插入的元素要比前面的元素大，位置正确跳出循环
            break;
        }
        
    }
}
print_r($arr3);
//Array ( [0] => 0 [1] => 1 [2] => 2 [3] => 3 [4] => 4 [5] => 6 [6] => 7 )

时间复杂度

在插入排序中，当待排序数组是有序时，此时是最优情况，即只需要和前一个数比较即可，这时比较只需要进行一次，时间复杂度是O（N）；
最坏的情况是待排序数组是逆序的，此时需要比较的次数是最多的，即插入排序最坏情况的时间复杂度是 O(N²)；
通常情况下，插入排序在平均情况下运行时间和最坏情况运行时间一样。

空间复杂度

插入排序的空间复杂度是常数阶 O（1）。

稳定性

如果待排序的序列中存在两个或两个以上具有相同关键词的数据，排序后这些数据的相对次序保持不变，即如果排序后两个相同的数的相对顺序不会发生改变，则该算法是稳定的；
如果排序后，数据的相对次序发生了变化，则该算法是不稳定的。关键词相同的数据元素将保持原有位置不变，所以该算法是稳定的。

`归并排序`

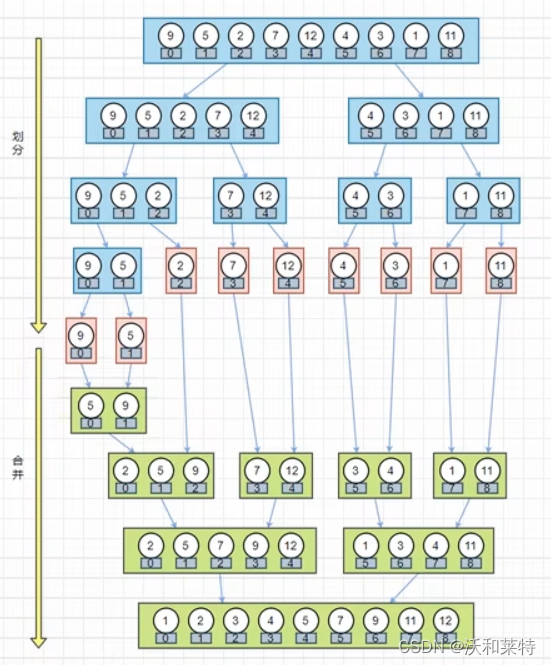
归并排序的原理：
将数组拆成两个数组；申请一个空间用于存放合并后的数组；
假设两个数组已经排好序列，设置两个指针，指针指向的位置分别是两个已经排好序的有序数列的数组的起始位置；
两指针分别指向两个数组的起始元素，并比较两个指针所指的元素，将较小的元素放入申请的空间；
然后将指针移动到下一位置；最后将另一个序列所剩的元素直接复制到合并序列中。

二路归并

$nums1=array(1,3,5);
$nums2=array(2,4,6);
// 申请空间用于存放合并后的数组
$nums3=array();
// 当需要合并的数组中含有元素，就进入循环
while(count($nums1) && count($nums2)){
    // 取出每个数组的第一个元素进行比较：array_shift() 函数删除数组中的第一个元素，并返回被删除元素的值。
    $nums3[]=$nums1[0]<$nums2[0]?array_shift($nums1):array_shift(($nums2));
}
// array_merge() 将一个或多个数组的单元合并起来，一个数组中的值附加在前一个数组的后面。返回作为结果的数组。
print_r(array_merge($nums3,$nums2,$nums1));//其中$nums1  $num2的顺序可颠倒
Array ( [0] => 1 [1] => 2 [2] => 3 [3] => 4 [4] => 5 [5] => 6 )

归并排序

通过二路归并的例子，归并排序就更容易理解了：

$arr4=array(2,4,1,3,6,5,0);
		function merge($arr4){
    $len=count($arr4);
    if($len<=1) return $arr4;
    $mid=floor($len/2);
// array_slice() 函数返回数组中的选定部分。
    $left=array_slice($arr4,0,$mid);
    $right=array_slice($arr4,$mid);
    // 如果分成的两个数组没有排好序，由于是奇数个元素的数组，无法均分成两个相同元素个数的数组
    // 最后在进行二路合并的时候就会乱序，因此需要对$left  $right进行排序
    // 调用merge函数  
    $left=merge($left);
    $right=merge($right);
    $arr5=array();
    while(count($left) && count($right)){
        $arr5[]=$left[0]<$right[0]?array_shift($left):array_shift($right);
    }
    return array_merge($arr5,$left,$right);
}
print_r(merge($arr4));
//Array ( [0] => 0 [1] => 1 [2] => 2 [3] => 3 [4] => 4 [5] => 5 [6] => 6 )

时间复杂度

归并排序比较占用内存，但却是一种效率高且稳定的算法。
改进归并排序在归并时先判断前段序列的最大值与后段序列最小值的关系再确定是否进行复制比较。如果前段序列的最大值小于等于后段序列最小值，则说明序列可以直接形成一段有序序列不需要再归并，反之则需要。所以在序列本身有序的情况下时间复杂度可以降至O(n)。

稳定性

归并排序是稳定的排序.即相等的元素的顺序不会改变

`查找算法`

顺序查找

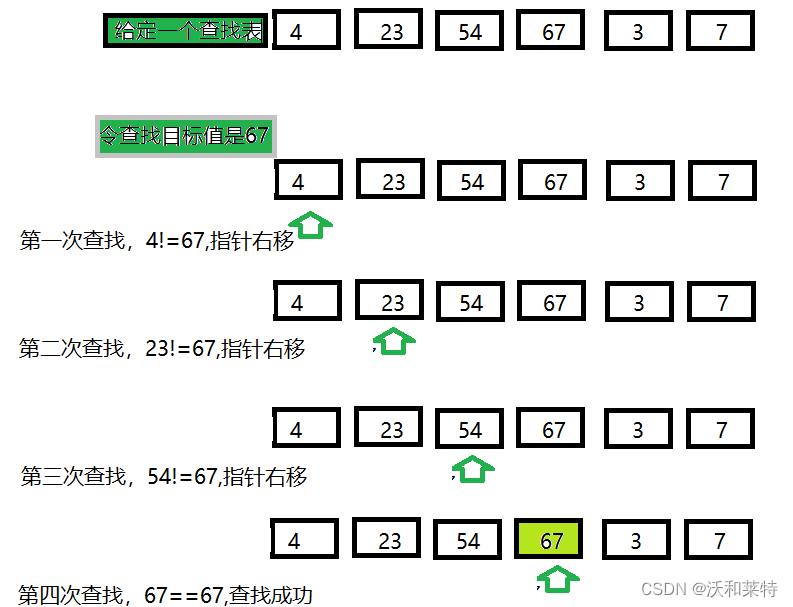
顺序查找也叫做线性查找，对于任意一个序列以及一个给定的元素，将给定元素与序列中元素依次比较，直到找出与给定关键字相同的元素，或者将序列中的元素与其都比较完为止。

$arr2=array(4,23,54,67,3,7);
function check($arr2,$num){
    for($i=0;$i<count($arr2);$i++){
        if($arr2[$i]==$num){
            return $arr2[$i];
        }
    }
    return false;
}
var_dump(check($arr2,3));
//int(3)

二分查找算法

//二分查找
		$arr=array(1,4,2,3,6,5,7);
		//得到数组边界
		$right = count ($arr);
		$left = 0;
		$res = 3;
		//循环匹配
		while($left <= $right){
		//得到中间位置
		$middle = floor(($right - $left) /2);
		//进行查找匹配
		if($arr[$middle] == $res){
			echo $middle + 1;
			break;
			}
		if($arr[$middle]<$res{
				$left =$middle + 1;
			}else{
			$right=$middle -  1;
			}
		}