1.数据的进制转化
- 进制的表示:二进制、十六进制,二进制符号位0b,一般表示为0b0011,十六进制符号位0x或H,可以表示为0x18F或18F
- R进制整数转十进制:位权展开法,用R进制数的每一位乘以R的n次方,n是变量,从R进制数的整数最低位开始,依次为0,1,2,…累加
- 十进制转R进制:十进制整数除以R倒取余数,用十进制数除以R,记录每次所得的余数,若商不为0,则继续除以R,直至商为0,然后将所有余数从下到上记录,排列成从左到右顺序,即转换后的R进制数
- m进制转n进制:先将m进制数转化为十进制数,再将十进制数转化为n进制数,中间需要通过十进制中转
- 二进制转八进制:每三位二进制数转换为一位八进制数,二进制数位个数不是三的倍数,则在前面补0(原则是数值不变),如二进制数01101有五位,前面补一位0就有六位,即001101,每三位转换为一位八进制数,即001=1,101=1+4=5,即01101=15
- 二进制转十六进制:每四位二进制数转换为一位十六进制数,二进制位数不是四的倍数,则在前面补0,如二进制数101101有六位,前面补两个0就有八位,即00101101,每四位数转换为一位十六进制,0010=2,1101=13=D,即101101=2D
2.数的表示
机器数:各种数值在计算机中表示的形式,其特点是使用二进制计数制,数的符号位0和1表示,小数点则隐含,不占位置
机器数有符号数和无符号数之分,无符号数表示整数,没有符号位,带符号数的最高位为符号位,整数符号位为0,负数符号位为1
定点表示法分为纯小数和纯整数两种,其中小数点不占存储位,而是按照以下约定:
纯小数:约定小数点的位置在机器数的最高位数值位之前
纯整数:约定小数点的位置在机器数的最低位数值为之后
真值:机器数对应的实际数值
3.数的编码方式
原码: 一个数的正常的二进制表示,最高位为符号,整数0的原码有两种形式:+0(0 0000000)和-0(10000000)
反码:正数的反码即原码;负数的反码是在原码的基础上,除符号位外,其他各位按位取反。数值0的反码也有两种形式:+0(00000000),-0(11111111)
补码:正数的补码即原码;负数的补码是在原码的基础上,除符号位外,其他各位按位取反,然后末位+1,若有进位则产生进位,因此数值0的补码只有一种形式:+0=-0=00000000
移码:用作浮点运算的阶码,无论是正数负数,都是将补码的首位(符号位)取反得到移码
机器字长为n时各种码制表示的符号位数的取值范围(差别在与0的表示,原码和反码分+0和-0,补码只有一个0,因此可以多表示一个)
例:若机器字长为8,请给出45和-45的原码、反码、补码和移码
| 真值 | 原码 | 反码 | 补码 | 移码 |
|---|---|---|---|---|
| 45 | 00101101 | 00101101 | 00101101 | 10101101 |
| -45 | 10101101 | 11010010 | 11010011 | 01010011 |
4 浮点数表示
浮点数:表示方法为N=F2E,其中E为阶码,F称为尾数,类似于十进制的科学计数法,如85.125=0.85125*102,二进制如:101.011=0.1010112^3
在浮点数的表示中,阶码为带符号的纯整数,尾数为带符号的纯小数,要注意符号位占最高位(正数0负数1),其表示格式如下:
很明显,与科学计数法类似,一个浮点数的表示方法不是唯一的,浮点数能表示数值范围由阶码确定,所表示的数值精度由尾数确定
尾数的表示采用规格化方法,即带符号尾数的补码必须为1.0xxx(负数)或者0.1xxx(正数),其中x可以为0或者1
浮点数运算步骤
- 对阶(使两个数的阶码相同,小阶向大阶看齐,叫嚣阶码增加即为,尾数就右移几位)
- 尾数计算(相加,若是减运算,则加负数)
- 结果规格化(即尾数表示规格化,带符号尾数转换为1.0xxx或者0.1xxx)
5 算数运算和逻辑运算
数与数之间的算术运算包括加减乘除等基本算术运算
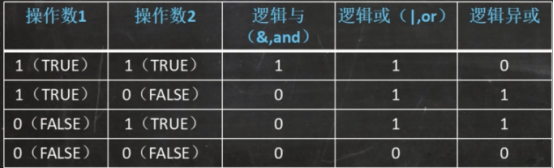
逻辑运算包括逻辑与&、逻辑或|、逻辑异或、逻辑左移<<、逻辑右移>>

逻辑与(又称为逻辑乘,类似于且,and):两个操作同时为真则为真,其中有一个为假则为假。
逻辑或(又称为逻辑加,类似于或,or):两个操作数只要其中一个为真,即为真。
逻辑异或:相异为真,相同为假。
逻辑非(NOT,类似于取反,!-):操作数为真,则结果为假;操作数为假,则结果为真。
真题:要判断字长为16位的整数a的低四位是否全为0,则(A)
- 将a与0x000F进行“逻辑与”运算,然后判断运算结果是否等于0
- 将a与0x000F进行“逻辑或”运算,然后判断运算结果是否等于F
- 将a与0xFFF0进行“逻辑异或”运算,然后判断运算结果是否等于0
- 将a与0xFFF0进行“逻辑与”运算,然后判断运算结果是否等于F
0x000F表示是十六进制,F也就是15,000F换成十六进制就是:0000 0000 0000 1111
0xFFF0换成十六进制即为:1111 1111 1111 0000。
一、先看A选项,a的高位为未知数,通过然后判断运算结果是否等于0,得出判断低四位是否全为0
(1)a与 0x000F逻辑与运算中,0x000F表示是十六进制,F也就是15,000F换成十六进制就是:0000 0000 0000 1111。又因为0和任何数作逻辑与运算都为0,所以a的高位与000F的高位作与运算,高位肯定是0(即000?)。
(2)看低位逻辑与运算,如果a的低四位有1,那么与000F中的F逻辑与运算,肯定是有1。如果a的低四位全是0,那么0000与F逻辑与,则全为0。
(3)选项A当选。
二、看B选项,a的高位为未知数,通过然后判断运算结果是否等于F,得出判断低四位是否全为0。
(1)a与 0x000F逻辑或运算中,任何数与1 作逻辑或运算都为1,a的高位与000F的高位作逻辑或运算中,高位不确定,可能是1,也可能是0。
(2)低四位与1111逻辑或运算中,同理不能确定,可能是1,也可能是0。排除B
三、先看C选项,a的高位为未知数,通过然后判断运算结果是否等于0,得出现在是判断低四位是否全为0。
(1)a与 0xFFF0逻辑异或运算中,0xFFF0换成十六进制即为:1111 1111 1111 0000
(2)相同为0,相异为1,高位不清楚,无法判断,排除C。
四、先看D选项,a的高位为未知数,通过然后判断运算结果是否等于F,得出判断低四位是否全为0。
(1)a与 0xFFF0逻辑与运算中,0xFFF0换成十六进制即为:1111 1111 1111 0000
(2)0xFFF0的低位是0,0与任何数逻辑与运算都为0,无法判断a的低位,排除D。
真题:对于逻辑表达式“x and y or not z”,and 、or、not分别是逻辑与、或、非运算,优先级从高到低位not、and、or,and、or为左结合,not为右结合,若进行短路计算,则(C)
- x为真时,整个表达式的值即为真,不需要计算y和z的值
- x为假时,整个表达式的值即为假,不需要计算y和z的值
- x为真时,根据y的值决定是否需要计算z的值
- x为假时,根据y的值决定是否需要计算z的值
(x and y)or (not z)
看选项A。A为真的时候,需要看Y的值决定,排除。
看选项B。A为假的时候,需要看z的值决定,排除。
看选项C。x为真的时候,需要看Y的值决定是否计算z,如果y为真,则不需要计算z。如果y为假,那么需要判断z是否为真,如果z为假,not z则为真,计算值。当选。
看选项D。X为假的时候,不需要看y的值(无论真假,都需要计算z的值),错误,排除。
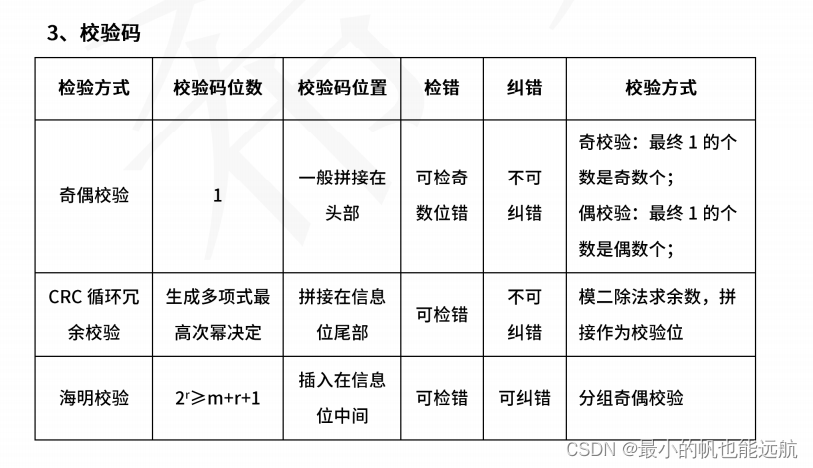
6.校验码