数值稳定性和模型初始化
- 数值稳定性
- 梯度不稳定的影响
- 推导
- 什么是梯度消失?
- 什么是梯度爆炸?
- 如何解决数值不稳定问题?——参数初始化
- 参数初始化的几种方法
- 默认初始化
- Xavier初始化
- 小结
当神经网络变得很深的时候,数值特别容易不稳定。
我们实现的每个模型都是根据某个预先指定的分布来初始化模型的参数。
初始化方案的选择在神经网络学习中起着举足轻重的作用, 它对保持数值稳定性至关重要
数值稳定性
梯度不稳定的影响
糟糕初始化参数可能会导致我们在训练时遇到梯度爆炸或梯度消失。
不稳定梯度带来的风险不止在于数值表示; 不稳定梯度也威胁到我们优化算法的稳定性。
- 梯度爆炸(gradient exploding)问题: 参数更新过大,破坏了模型的稳定收敛;
- 梯度消失(gradient vanishing)问题: 参数更新过小,在每次更新时几乎不会移动,导致模型无法学习。
推导
考虑一个具有
L
L
L层、输入
x
x
x和输出
o
o
o的深层网络。每一层
l
l
l由变换
f
l
f_l
fl定义, 该变换的参数为权重
W
(
l
)
W^{(l)}
W(l), 其隐藏变量是
h
(
l
)
h^{(l)}
h(l)(令
h
0
=
x
h^{0} = x
h0=x)。
该网络可以表示为:
h
(
l
)
=
f
l
(
h
(
l
−
1
)
)
因此
o
=
f
L
∘
…
∘
f
1
(
x
)
.
\mathbf{h}^{(l)} = f_l (\mathbf{h}^{(l-1)}) \text{ 因此 } \mathbf{o} = f_L \circ \ldots \circ f_1(\mathbf{x}).
h(l)=fl(h(l−1)) 因此 o=fL∘…∘f1(x).
如果所有隐藏变量和输入都是向量, 我们可以将
o
\mathbf{o}
o关于任何一组参数
W
(
l
)
\mathbf{W}^{(l)}
W(l)的梯度写为下式:
∂
W
(
l
)
o
=
∂
h
(
L
−
1
)
h
(
L
)
⏟
M
(
L
)
=
d
e
f
⋅
…
⋅
∂
h
(
l
)
h
(
l
+
1
)
⏟
M
(
l
+
1
)
=
d
e
f
∂
W
(
l
)
h
(
l
)
⏟
v
(
l
)
=
d
e
f
.
\partial_{\mathbf{W}^{(l)}} \mathbf{o} = \underbrace{\partial_{\mathbf{h}^{(L-1)}} \mathbf{h}^{(L)}}_{ \mathbf{M}^{(L)} \stackrel{\mathrm{def}}{=}} \cdot \ldots \cdot \underbrace{\partial_{\mathbf{h}^{(l)}} \mathbf{h}^{(l+1)}}_{ \mathbf{M}^{(l+1)} \stackrel{\mathrm{def}}{=}} \underbrace{\partial_{\mathbf{W}^{(l)}} \mathbf{h}^{(l)}}_{ \mathbf{v}^{(l)} \stackrel{\mathrm{def}}{=}}.
∂W(l)o=M(L)=def
∂h(L−1)h(L)⋅…⋅M(l+1)=def
∂h(l)h(l+1)v(l)=def
∂W(l)h(l).
该梯度是
L
−
l
L-l
L−l个矩阵
M
(
L
)
⋅
…
⋅
M
(
l
+
1
)
\mathbf{M}^{(L)} \cdot \ldots \cdot \mathbf{M}^{(l+1)}
M(L)⋅…⋅M(l+1)与梯度向量
v
(
l
)
\mathbf{v}^{(l)}
v(l)的乘积。
因此,我们容易受到数值下溢问题的影响. 当将太多的概率乘在一起时,这些问题经常会出现。
什么是梯度消失?
激活函数sigmoid函数,
1
/
(
1
+
exp
(
−
x
)
)
1/(1 + \exp(-x))
1/(1+exp(−x)),类似于阈值函数。 由于早期的人工神经网络受到生物神经网络的启发, 神经元要么完全激活要么完全不激活(就像生物神经元)的想法很有吸引力。 然而,它却是导致梯度消失问题的一个常见的原因:
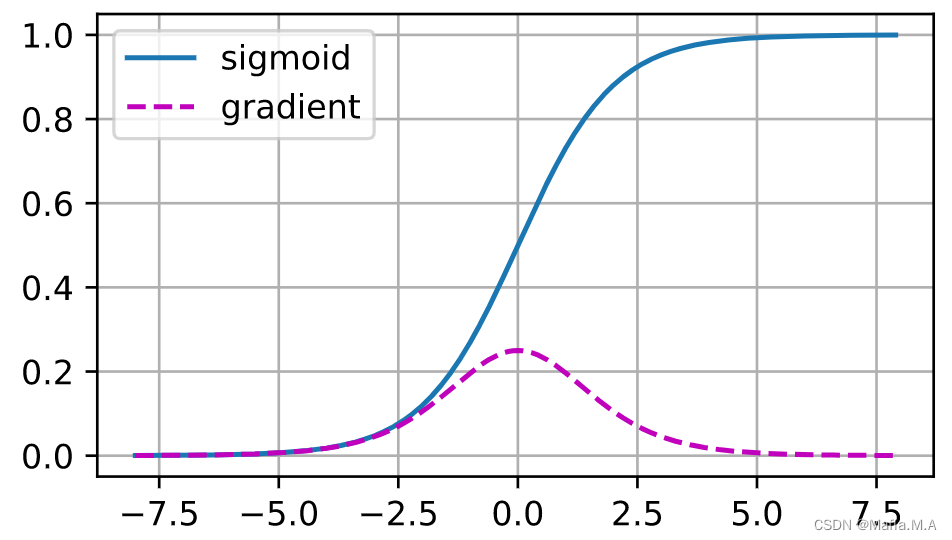
当sigmoid函数的输入很大或是很小时,它的梯度都会消失。当反向传播通过许多层时,除非我们在刚刚好的地方, 这些地方sigmoid函数的输入接近于零,否则整个乘积的梯度可能会消失。
当我们的网络有很多层时,除非我们很小心,否则在某一层可能会切断梯度。
更稳定的ReLU系列函数已经成为从业者的默认选择。
什么是梯度爆炸?
矩阵乘积发生了爆炸,这种情况是由于深度网络的初始化导致的,没有机会让梯度下降优化器收敛。
#pytorch
M = torch.normal(0, 1, size=(4,4))
print('一个矩阵 \n',M)
for i in range(100):
M = torch.mm(M,torch.normal(0, 1, size=(4, 4)))
print('乘以100个矩阵后\n', M)

如何解决数值不稳定问题?——参数初始化
参数初始化是解决(或至少减轻)上述问题的一种方法, 优化期间的注意和适当的正则化也可以进一步提高稳定性。
参数初始化的几种方法
默认初始化
如果我们不指定初始化方法, 框架将使用默认的随机初始化方法,对于中等难度的问题,这种方法通常很有效。
Xavier初始化
某些没有非线性的全连接层输出(例如,隐藏变量)
o
i
o_{i}
oi的尺度分布。 对于该层
n
i
n
n_\mathrm{in}
nin输入
x
j
x_j
xj及其相关权重
w
i
j
w_{ij}
wij,输出由下式给出
o
i
=
∑
j
=
1
n
i
n
w
i
j
x
j
.
o_{i} = \sum_{j=1}^{n_\mathrm{in}} w_{ij} x_j.
oi=j=1∑ninwijxj.
现在标准且实用的Xavier初始化的基础, 它以其提出者 (Glorot and Bengio, 2010) 第一作者的名字命名。 通常,Xavier初始化从均值为零,方差
σ
2
=
2
n
i
n
+
n
o
u
t
\sigma^2 = \frac{2}{n_\mathrm{in} + n_\mathrm{out}}
σ2=nin+nout2的高斯分布中采样权重。 我们也可以将其改为选择从均匀分布中抽取权重时的方差。 注意均匀分布
U
(
−
a
,
a
)
U(-a, a)
U(−a,a)的方差为
a
2
3
\frac{a^2}{3}
3a2。 将
a
2
3
\frac{a^2}{3}
3a2代入到
σ
2
\sigma^2
σ2的条件中,将得到初始化值域:
U
(
−
6
n
i
n
+
n
o
u
t
,
6
n
i
n
+
n
o
u
t
)
.
U\left(-\sqrt{\frac{6}{n_\mathrm{in} + n_\mathrm{out}}}, \sqrt{\frac{6}{n_\mathrm{in} + n_\mathrm{out}}}\right).
U(−nin+nout6,nin+nout6).
尽管在上述数学推理中,“不存在非线性”的假设在神经网络中很容易被违反, 但Xavier初始化方法在实践中被证明是有效的。
小结
- 梯度消失和梯度爆炸是深度网络中常见的问题。在参数初始化时需要非常小心,以确保梯度和参数可以得到很好的控制。
- 需要用启发式的初始化方法来确保初始梯度既不太大也不太小。
- ReLU激活函数缓解了梯度消失问题,这样可以加速收敛。
- 随机初始化是保证在进行优化前打破对称性的关键。
- Xavier初始化表明,对于每一层,输出的方差不受输入数量的影响,任何梯度的方差不受输出数量的影响。