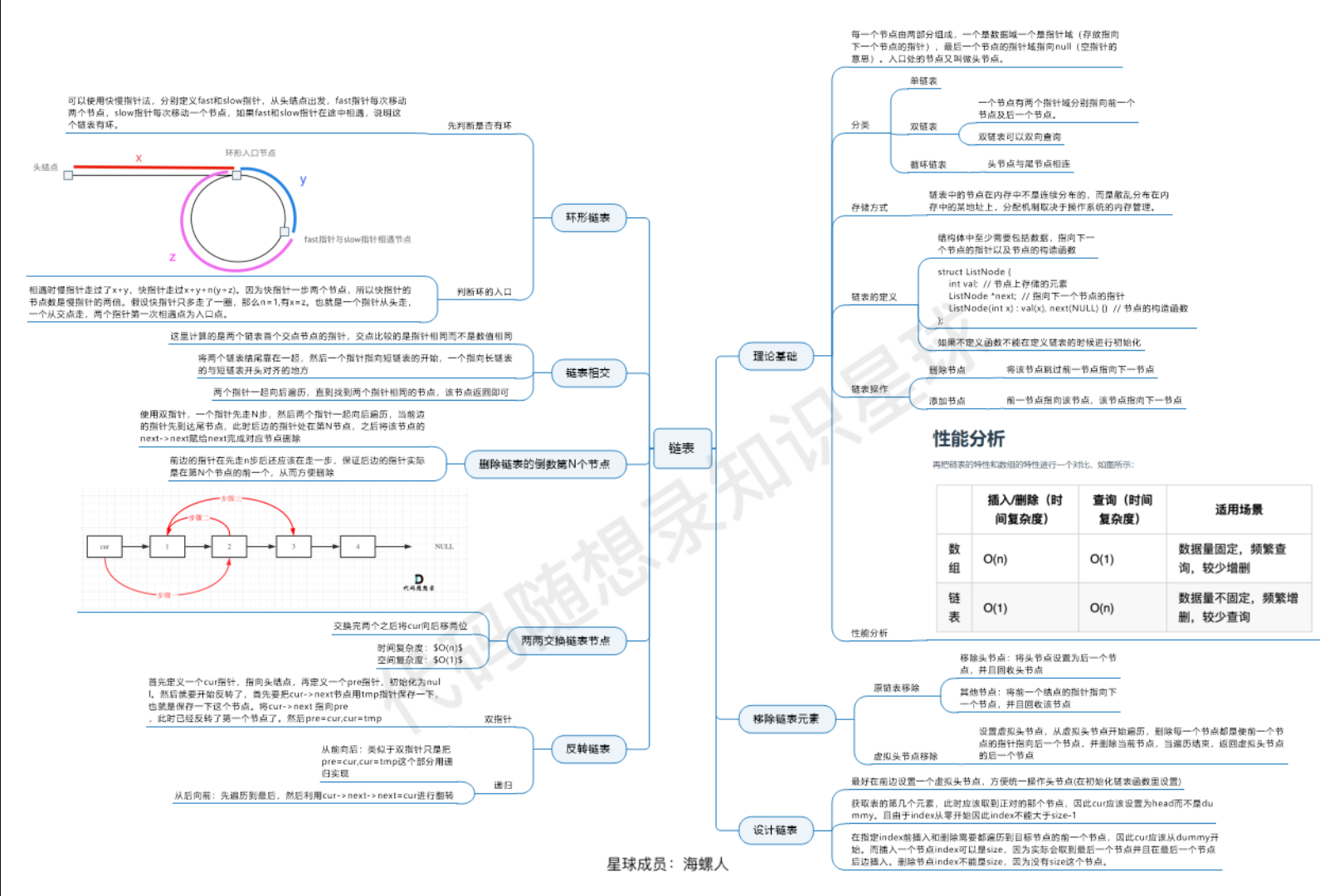
二叉树的种类
在我们解题过程中二叉树有两种主要的形式:满二叉树和完全二叉树
满二叉树
满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
如图所示:

这棵二叉树为满二叉树,也可以说深度为k,有2^k-1个节点的二叉树。
完全二叉树
什么是完全二叉树?
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。
大家要自己看完全二叉树的定义,很多同学对完全二叉树其实不是真正的懂了。
我来举一个典型的例子如题:
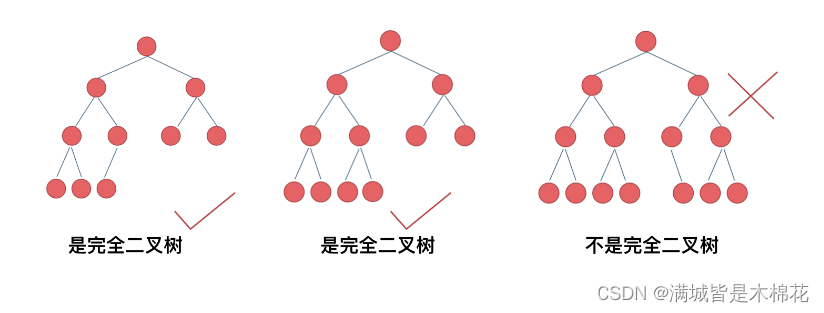
相信不少同学最后一个二叉树是不是完全二叉树都中招了。
之前我们刚刚讲过优先级队列其实是一个堆,堆就是一棵完全二叉树,同时保证父子节点的顺序关系。
二叉搜索树
前面介绍的树,都没有数值的,而二叉搜索树是有数值的了,二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
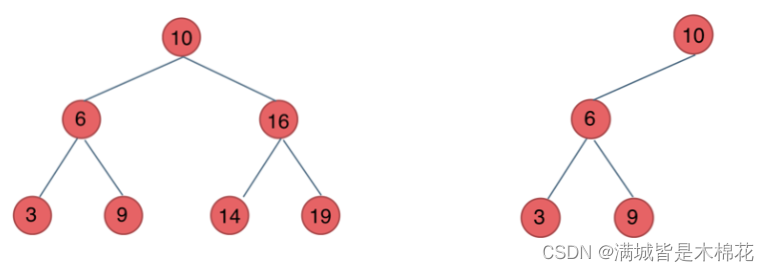
下面这两棵树都是搜索树
平衡二叉搜索树
平衡二叉搜索树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
如图:
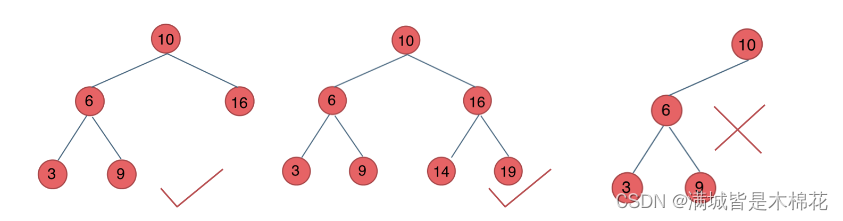
最后一棵 不是平衡二叉树,因为它的左右两个子树的高度差的绝对值超过了1。
C++中map、set、multimap,multiset的底层实现都是平衡二叉搜索树,所以map、set的增删操作时间时间复杂度是logn,注意我这里没有说unordered_map、unordered_set,unordered_map、unordered_map底层实现是哈希表。
所以大家使用自己熟悉的编程语言写算法,一定要知道常用的容器底层都是如何实现的,最基本的就是map、set等等,否则自己写的代码,自己对其性能分析都分析不清楚!
二叉树的存储方式
二叉树可以链式存储,也可以顺序存储。
那么链式存储方式就用指针, 顺序存储的方式就是用数组。
顾名思义就是顺序存储的元素在内存是连续分布的,而链式存储则是通过指针把分布在各个地址的节点串联一起。
链式存储如图:
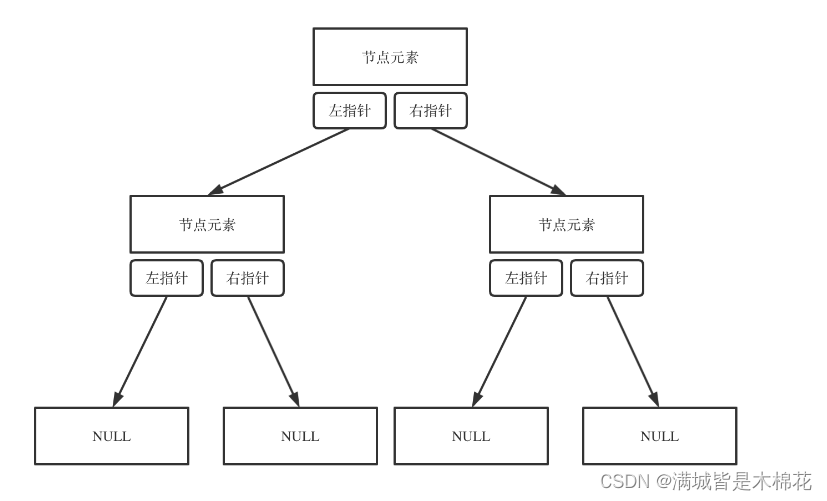
链式存储是大家很熟悉的一种方式,那么我们来看看如何顺序存储呢?
其实就是用数组来存储二叉树,顺序存储的方式如图:
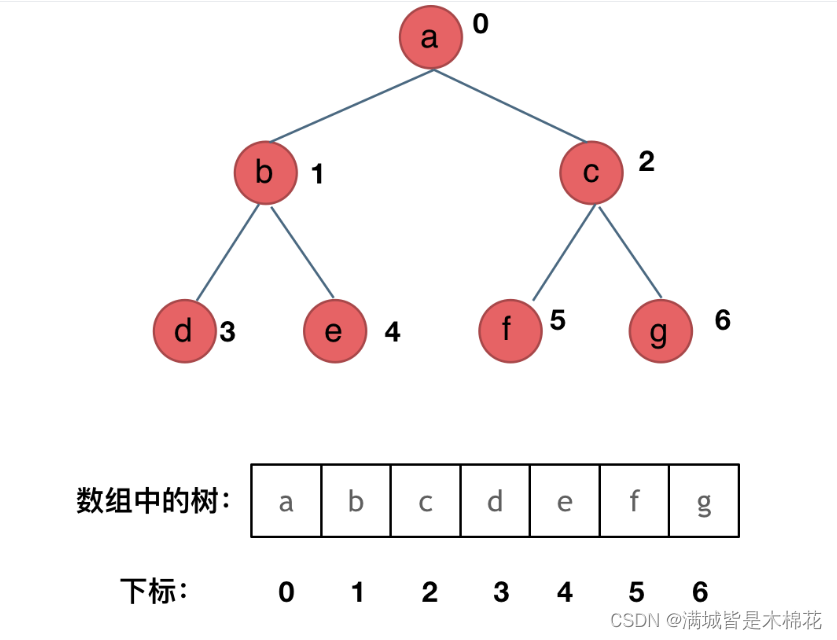
用数组来存储二叉树如何遍历的呢?
如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
但是用链式表示的二叉树,更有利于我们理解,所以一般我们都是用链式存储二叉树。
所以大家要了解,用数组依然可以表示二叉树。
二叉树的遍历方式
关于二叉树的遍历方式,要知道二叉树遍历的基本方式都有哪些。
一些同学用做了很多二叉树的题目了,可能知道前中后序遍历,可能知道层序遍历,但是却没有框架。
我这里把二叉树的几种遍历方式列出来,大家就可以一一串起来了。
二叉树主要有两种遍历方式:
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历。
这两种遍历是图论中最基本的两种遍历方式,后面在介绍图论的时候 还会介绍到。
那么从深度优先遍历和广度优先遍历进一步拓展,才有如下遍历方式:
- 深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历
- 层次遍历(迭代法)
在深度优先遍历中:有三个顺序,前中后序遍历, 有同学总分不清这三个顺序,经常搞混,我这里教大家一个技巧。
这里前中后,其实指的就是中间节点的遍历顺序,只要大家记住 前中后序指的就是中间节点的位置就可以了。
看如下中间节点的顺序,就可以发现,中间节点的顺序就是所谓的遍历方式
- 前序遍历:中左右
- 中序遍历:左中右
- 后序遍历:左右中
大家可以对着如下图,看看自己理解的前后中序有没有问题。
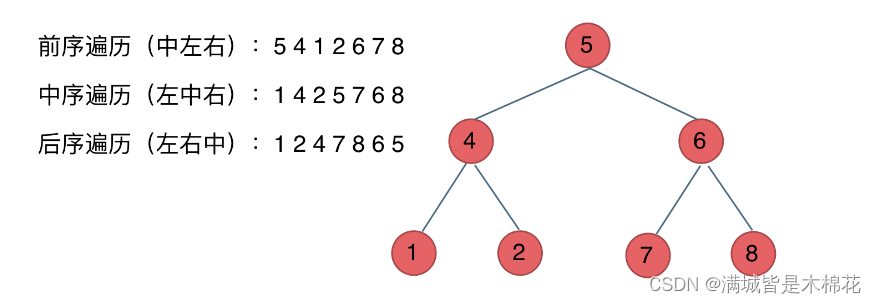
最后再说一说二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
之前我们讲栈与队列的时候,就说过栈其实就是递归的一种实现结构,也就说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。
而广度优先遍历的实现一般使用队列来实现,这也是队列先进先出的特点所决定的,因为需要先进先出的结构,才能一层一层的来遍历二叉树。
这里其实我们又了解了栈与队列的一个应用场景了。
具体的实现我们后面都会讲的,这里大家先要清楚这些理论基础。
二叉树的定义
刚刚我们说过了二叉树有两种存储方式顺序存储,和链式存储,顺序存储就是用数组来存,这个定义没啥可说的,我们来看看链式存储的二叉树节点的定义方式。
C++代码如下:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};大家会发现二叉树的定义 和链表是差不多的,相对于链表 ,二叉树的节点里多了一个指针, 有两个指针,指向左右孩子。
这里要提醒大家要注意二叉树节点定义的书写方式。
在现场面试的时候 面试官可能要求手写代码,所以数据结构的定义以及简单逻辑的代码一定要锻炼白纸写出来。
因为我们在刷leetcode的时候,节点的定义默认都定义好了,真到面试的时候,需要自己写节点定义的时候,有时候会一脸懵逼!
其他语言版本
JavaScript:
function TreeNode(val, left, right) {
this.val = (val===undefined ? 0 : val)
this.left = (left===undefined ? null : left)
this.right = (right===undefined ? null : right)
}Java:
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}Python:
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None