🚀write in front🚀
📜所属专栏：
🛰️博客主页：睿睿的博客主页
🛰️代码仓库：🎉VS2022_C语言仓库
🎡您的点赞、关注、收藏、评论，是对我最大的激励和支持！！！
关注我，关注我，关注我，你们将会看到更多的优质内容！！

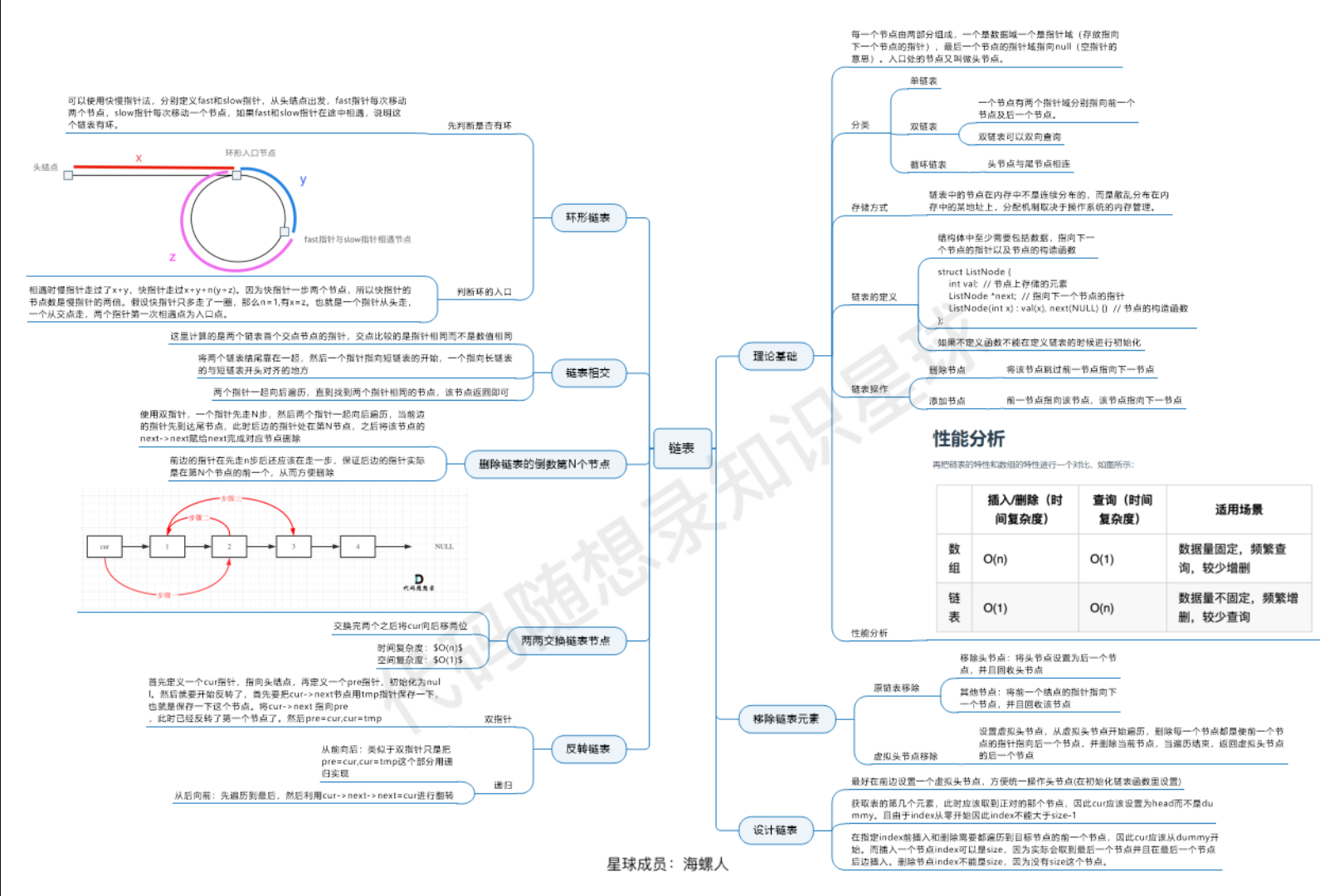
1.数据类型介绍

我们知道，数据类型的意义是：

• 类型决定了开辟内存空间的大小。

• 类型决定了看待内存空间的视角（后面整形和浮点在内存中存储的差异就可以看出）

1.1类型的基本归类：

整形家族：

char unsigned
char signed char

short
unsigned short [int]
signed short [int]

int unsigned
int signed int

long unsigned long [int] signed long [int]

注意：
char虽然是字符形式，但是存储的确实ASCII码值，而ASCII码是整形，所以char归于整形。

浮点型家族：

float
double

指针类型：

int pi;
char pc;
float pf;
void pv;

2.整形在内存中的存储

2.1原码，反码，补码：

  计算机中的整数有三种2进制表示方法，即 原码、反码和补码 。

原码
直接将数值按照正负数的形式翻译成二进制就可以得到原码。
反码
将原码的符号位不变，其他位依次按位取反就可以得到反码。
补码
反码+1就得到补码。

注意：

1.三种表示方法均有符号位和数值位两部分，符号位都是用 0表示“正”，用 1表示“负”，而数值位
2正数的原、反、补码都相同。
3.负整数的三种表示方法各不相同。

对于整形来说，数据存放在内存中存的是补码，为什么呢？

原来，在计算机系统中，数值一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统
一处理；
同时，加法和减法也可以统一处理（CPU只有加法器）此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

2.2原码，反码，补码的相互转换：

我们只要记住:取反+1即可实现原码与补码的相互转换:

举一个例子：

int a = 20;
正数的原码反码补码相同
原码：00000000 00000000 00000000 00010100
反码：00000000 00000000 00000000 00010100
补码：00000000 00000000 00000000 00010100
int b = -10;
原码：10000000 00000000 00000000 00001010
反码：11111111 11111111 11111111 11110101 ----符号位不变，其他按位取反
补码：11111111 11111111 11111111 11110110 ----反码+1

2.3.大小端介绍：

  我们知道栈区是从高地址往低地址开始存变量，那么整形变量里的四个字节是怎么排序的呢，这里就涉及到了大小端的介绍。

大端（存储）模式，是指数据的低位保存在内存的高地址中，而数据的高位，保存在内存的低地址
中；
小端（存储）模式，是指数据的低位保存在内存的低地址中，而数据的高位,，保存在内存的高地址中。

我们来看看vs2022的小端模式就会清楚很多！

我们知道a的16进制是00 00 00 14，由图我们可以看出，数据的低位存在了内存的低地址，高位则存在了高地址，这就是小端的处理。

2.4如何判断大小端（百度笔试题）

  我们可以通过1存入内存中在大小端字节存储的差异来判断大小端，我们知道，指针的类型决定了他能访问的空间，我们用char类型数组访问，小端的访问出01，大端访问出00，这就是区别所在，我们来看看代码：

int check_sys()
{
	int a = 1;
    //char *p=(char*)&a;
    //return *p;
	return *(char*)&a;
}
int main()
{
	int ret = check_sys();
	if (1 == ret)
	{
		printf("小端\n");
	}
	else
	{
		printf("大端\n");
	}
	return 0;
} 

3.表达式求值

3.1.隐式类型转换：

表达式中的字符和短整形操作数在使用之前都会被转换为普通整形（int)类型，这种转换称为整形提升。

那么电脑是如何整形提升的呢？

负数和正数的整形提升：
补最高位
eg:
char c=-1;
11111111
111111111111111111111111111111111111111
char b=1;
0000001
0000000000000000000000000000000001
无符号的整形提升：
高位补0

例子1：

int main()
{
char a = 0xb6;
short b = 0xb600;
int c = 0xb6000000;
if(a==0xb6)
printf("a");
if(b==0xb600)
printf("b");
if(c==0xb6000000)
printf("c");
return 0;
}

实例1中的a,b要进行整形提升,但是c不需要整形提升

a的二进制是 0000 0000 1001 0110

截断后是 1001 0110

整形提升后是1111 1111 1001 0110

反码1000 0000 0110 1001

原码1000 0000 0110 1010

a,b整形提升之后,变成了负数,结果是假,但是c不发生整形提升,则表达式的结果是真.
所程序输出的结果是:c

例子2：

int main()
{
char c = 1;
printf("%u\n", sizeof(c));
printf("%u\n", sizeof(+c));
printf("%u\n", sizeof(-c));
return 0;
}

  实例2中的,c只要参与表达式运算,就会发生整形提升,表达式 +c ,就会发生提升,所以 sizeof(+c) 是4个字节.
  表达式 -c 也会发生整形提升,所以 sizeof(-c) 是4个字节,但是 sizeof c ,就是1个字节

3.2算术转化：

如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。如果某个操作数的类型在上面这个列表中排名较低，那么首先要转换为另外一个操作数的类型后执行运算。排名顺序如下：

4.整形存储的例子

例子1：

a和b都是有符号char
10000000000000000000000000000001
11111111111111111111111111111110
11111111111111111111111111111111
11111111 - a 截断
11111111111111111111111111111111 - 提升
c是无符号char，提升的时候补0
10000000000000000000000000000001
11111111111111111111111111111110
11111111111111111111111111111111
00000000000000000000000011111111
答案是a=-1，b=-1，c=255

注意：

  %d在读取时会读取符号位，而%u在读取时不会读取符号位！

例子2：

-128的原反补如下：
10000000000000000000000010000000
11111111111111111111111101111111
11111111111111111111111110000000 -128的补码
10000000 - a
整形提升后：
11111111111111111111111110000000
以%u的视角读取时，不会读出符号位，所以答案是一个很大的数字4,294,967,168。

例子3：

128的原反补如下：
00000000000000000000000010000000
01111111111111111111111101111111
01111111111111111111111110000000 -128的补码
10000000 - a
整形提升后：
11111111111111111111111110000000
以%u的视角读取时，不会读出符号位，所以答案是一个很大的数字4,294,967,168。

例子4：

int i = -20
10000000000000000000000000010100
11111111111111111111111111101011
11111111111111111111111111101100
unsign int j=10；
00000000000000000000000000001010
相加得：
11111111111111111111111111110110 - 补码
11111111111111111111111111110101
10000000000000000000000000001010
答案是-10

例子5：

我们知道unsigned int的范围一定是大于等于0的，所以当无符号的i=0时–会得到非常大的数字，会变成一个死循环，
因为0-1等于-1，
-1的补码为1111111111111111
而无符号数不看符号位，所以是很大的数4,294,967,295
具体循环为：
9 8 7 6 5 4 3 2 1 0 4,294,967,295 4,294,967,294…

例子6：

补充：

我们知道有符号char的范围是-128到127并且是一个轮回（因为超出范围后截断，还是在这个范围内）

  所以这一题目的循环是-1 -2…-128 127 126 125…0 -1 -2 -3…-128 127—而我们知道，strlen在发现\0就会停止，所以a数组的长度为255.

例子7：

一样的，我们知道无符号char的范围是0到255，所以当i=255时再加1，会进1，使截断后全为0，所以255+1以后又变成0，又是一个死循环了。

总结

本站主要讲解了数据的基本类型、原码反码补码、大小端和整型的存储

这里我们额外要记住的是：

整型提升补的数字是又变量类型决定的，%d和%u只是决定了读取的时候是否读取符号位。

如果对你有帮助，不要忘记点赞加收藏哦！！！

想获得更多优质的博客，一定不要忘记关注我哦！！！

  更新不易，辛苦各位小伙伴们动动小手，👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要！最后，本文仍有许多不足之处，欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正！

专栏订阅：
每日一题
c语言学习
算法
智力题
更新不易，辛苦各位小伙伴们动动小手，👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要！最后，本文仍有许多不足之处，欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正！