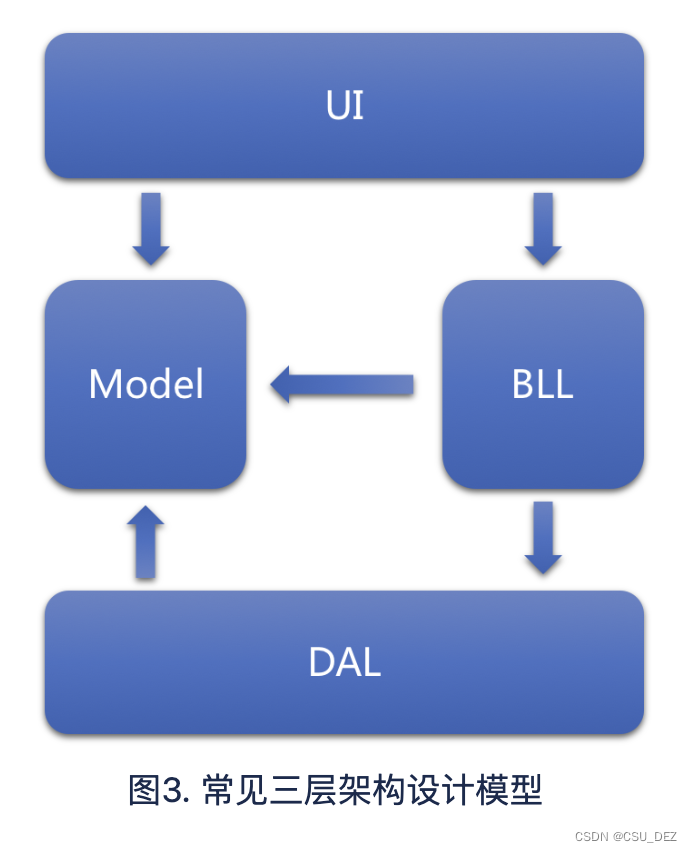
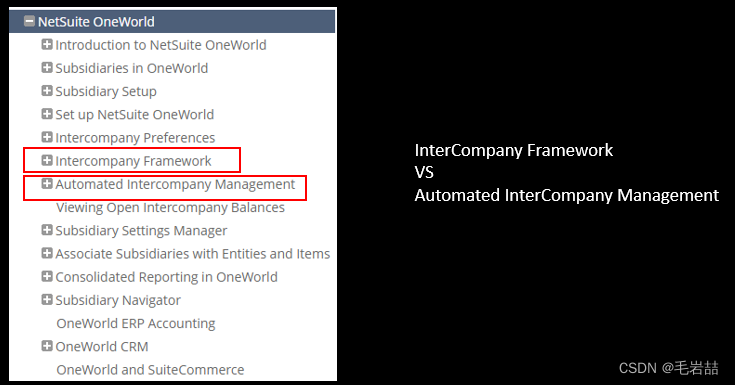
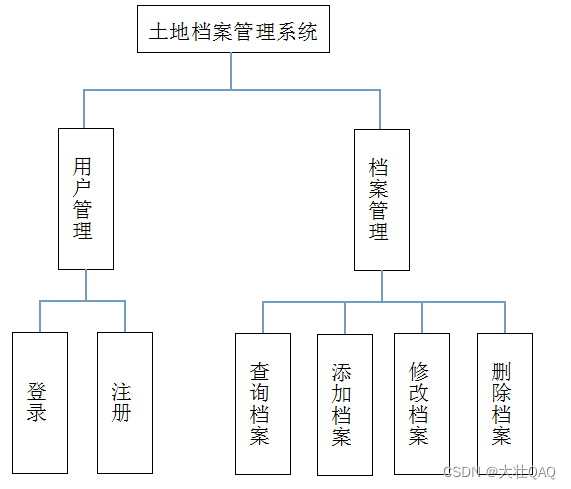
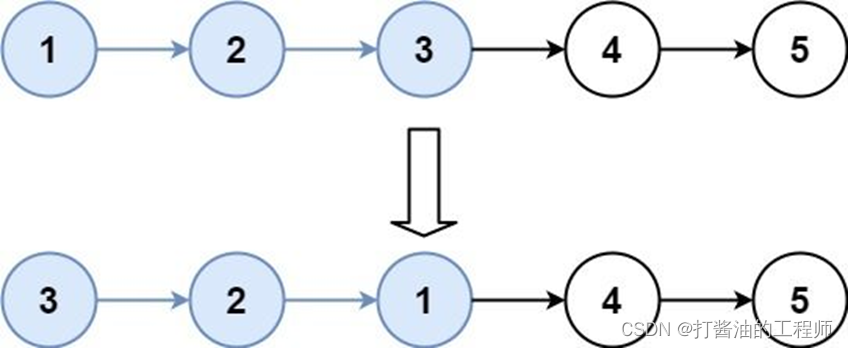
各种文本编辑器的"查找"功能(Ctrl+F),大多采用Boyer-Moore算法,效率非常高。
算法简介
在 1977 年,Robert S. Boyer (Stanford Research Institute) 和 J Strother Moore (Xerox Palo Alto Research Center) 共同发表了文章《A Fast String Searching Algorithm》,介绍了一种新的快速字符串匹配算法。这种算法在逻辑上相对于现有的算法有了显著的改进,它对要搜索的字符串进行倒序的字符比较,并且当字符比较不匹配时无需对整个模式串再进行搜索。
Boyer-Moore 算法的主要特点有:
对模式字符的比较顺序时从右向左;
预处理需要 O(m + σ) 的时间和空间复杂度;
匹配阶段需要 O(m × n) 的时间复杂度;
匹配阶段在最坏情况下需要 3n 次字符比较;
最优复杂度 O(n/m);
在 Naive 算法中,对文本 T 和模式 P 字符串均未做预处理。而在 KMP 算法中则对模式 P 字符串进行了预处理操作,以预先计算模式串中各位置的最长相同前后缀长度的数组。Boyer–Moore 算法同样也是对模式 P 字符串进行预处理。
我们知道,在 Naive 算法中,如果发现模式 P 中的字符与文本 T 中的字符不匹配时,需要将文本 T 的比较位置向后滑动一位,模式 P 的比较位置归 0 并从头开始比较。而 KMP 算法则是根据预处理的结果进行判断以使模式 P 的比较位置可以向后滑动多个位置。Boyer–Moore 算法的预处理过程也是为了达到相同效果。
Boyer–Moore 算法在对模式 P 字符串进行预处理时,将采用两种不同的启发式方法。这两种启发式的预处理方法称为:
坏字符(Bad Character Heuristic):当文本 T 中的某个字符跟模式 P 的某个字符不匹配时,我们称文本 T 中的这个失配字符为坏字符。
好后缀(Good Suffix Heuristic):当文本 T 中的某个字符跟模式 P 的某个字符不匹配时,我们称文本 T 中的已经匹配的字符串为好后缀。
Boyer–Moore 算法在预处理时,将为两种不同的启发法结果创建不同的数组,分别称为 Bad-Character-Shift(or The Occurrence Shift)和 Good-Suffix-Shift(or Matching Shift)。当进行字符匹配时,如果发现模式 P 中的字符与文本 T 中的字符不匹配时,将比较两种不同启发法所建议的移动位移长度,选择最大的一个值来对模式 P 的比较位置进行滑动。
此外,Naive 算法和 KMP 算法对模式 P 的比较方向是从前向后比较,而 Boyer–Moore 算法的设计则是从后向前比较,即从尾部向头部方向进行比较。
图例分析
例子来源于阮一峰的 字符串匹配的Boyer-Moore算法
下面,我根据Moore教授自己的例子来解释这种算法。

假定字符串为"HERE IS A SIMPLE EXAMPLE",搜索词为"EXAMPLE"。

首先,"字符串"与"搜索词"头部对齐,从尾部开始比较。
这是一个很聪明的想法,因为如果尾部字符不匹配,那么只要一次比较,就可以知道前7个字符(整体上)肯定不是要找的结果。
我们看到,"S"与"E"不匹配。这时,"S"就被称为"坏字符"(bad character),即不匹配的字符。我们还发现,"S"不包含在搜索词"EXAMPLE"之中,这意味着可以把搜索词直接移到"S"的后一位。

依然从尾部开始比较,发现"P"与"E"不匹配,所以"P"是"坏字符"。但是,"P"包含在搜索词"EXAMPLE"之中。所以,将搜索词后移两位,两个"P"对齐。
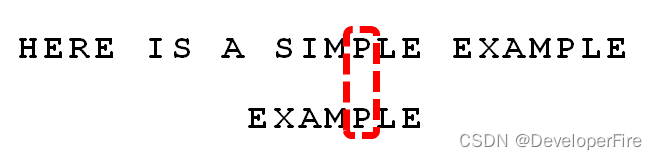
我们由此总结出"坏字符规则":
后移位数 = 坏字符的位置 - 搜索词中的上一次出现位置
如果"坏字符"不包含在搜索词之中,则上一次出现位置为 -1。
以"P"为例,它作为"坏字符",出现在搜索词的第6位(从0开始编号),在搜索词中的上一次出现位置为4,所以后移 6 - 4 = 2位。再以前面第二步的"S"为例,它出现在第6位,上一次出现位置是 -1(即未出现),则整个搜索词后移 6 - (-1) = 7位。

依然从尾部开始比较,"E"与"E"匹配。
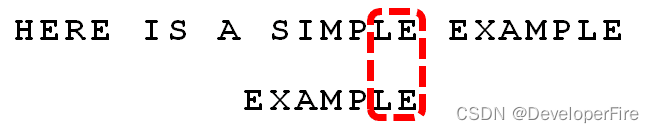
比较前面一位,"LE"与"LE"匹配。
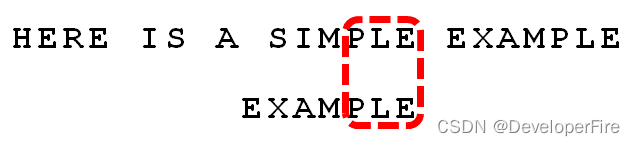
比较前面一位,"PLE"与"PLE"匹配。

比较前面一位,"MPLE"与"MPLE"匹配。我们把这种情况称为"好后缀"(good suffix),即所有尾部匹配的字符串。注意,"MPLE"、"PLE"、"LE"、"E"都是好后缀。
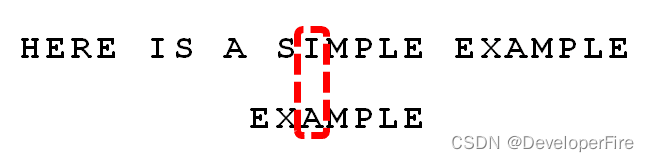
比较前一位,发现"I"与"A"不匹配。所以,"I"是"坏字符"。
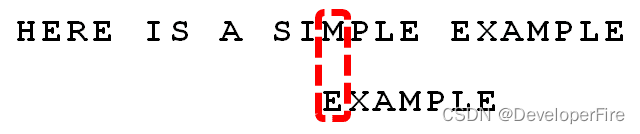
根据"坏字符规则",此时搜索词应该后移 2 - (-1)= 3 位。问题是,此时有没有更好的移法?

我们知道,此时存在"好后缀"。所以,可以采用"好后缀规则":
后移位数 = 好后缀的位置 - 搜索词中的上一次出现位置
举例来说,如果字符串"ABCDAB"的后一个"AB"是"好后缀"。那么它的位置是5(从0开始计算,取最后的"B"的值),在"搜索词中的上一次出现位置"是1(第一个"B"的位置),所以后移 5 - 1 = 4位,前一个"AB"移到后一个"AB"的位置。
再举一个例子,如果字符串"ABCDEF"的"EF"是好后缀,则"EF"的位置是5 ,上一次出现的位置是 -1(即未出现),所以后移 5 - (-1) = 6位,即整个字符串移到"F"的后一位。
这个规则有三个注意点:
"好后缀"的位置以最后一个字符为准。假定"ABCDEF"的"EF"是好后缀,则它的位置以"F"为准,即5(从0开始计算)。
如果"好后缀"在搜索词中只出现一次,则它的上一次出现位置为 -1。比如,"EF"在"ABCDEF"之中只出现一次,则它的上一次出现位置为-1(即未出现)。
如果"好后缀"有多个,则除了最长的那个"好后缀",其他"好后缀"的上一次出现位置必须在头部。比如,假定"BABCDAB"的"好后缀"是"DAB"、"AB"、"B",请问这时"好后缀"的上一次出现位置是什么?回答是,此时采用的好后缀是"B",它的上一次出现位置是头部,即第0位。这个规则也可以这样表达:如果最长的那个"好后缀"只出现一次,则可以把搜索词改写成如下形式进行位置计算"(DA)BABCDAB",即虚拟加入最前面的"DA"。
回到上文的这个例子。此时,所有的"好后缀"(MPLE、PLE、LE、E)之中,只有"E"在"EXAMPLE"还出现在头部,所以后移 6 - 0 = 6位。

可以看到,"坏字符规则"只能移3位,"好后缀规则"可以移6位。所以,Boyer-Moore算法的基本思想是,每次后移这两个规则之中的较大值。
更巧妙的是,这两个规则的移动位数,只与搜索词有关,与原字符串无关。因此,可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时,只要查表比较一下就可以了。

继续从尾部开始比较,"P"与"E"不匹配,因此"P"是"坏字符"。根据"坏字符规则",后移 6 - 4 = 2位。

从尾部开始逐位比较,发现全部匹配,于是搜索结束。如果还要继续查找(即找出全部匹配),则根据"好后缀规则",后移 6 - 0 = 6位,即头部的"E"移到尾部的"E"的位置。
从上面的示例描述可以看出,Boyer–Moore 算法的精妙之处在于,其通过两种启示规则来计算后移位数,且其计算过程只与模式 P 有关,而与文本 T 无关。因此,在对模式 P 进行预处理时,可预先生成 "坏字符规则之向后位移表" 和 "好后缀规则之向后位移表",在具体匹配时仅需查表比较两者中最大的位移即可。