项目场景一：

• 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

• 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

---

问题描述

• 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

• 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

---

示例分析：

• 输入： 3
• 输出： 3
• 解释： 有三种方法可以爬到楼顶。1. 1 阶 + 1 阶 + 1 阶2. 1 阶 + 2 阶3. 2 阶 + 1 阶

---

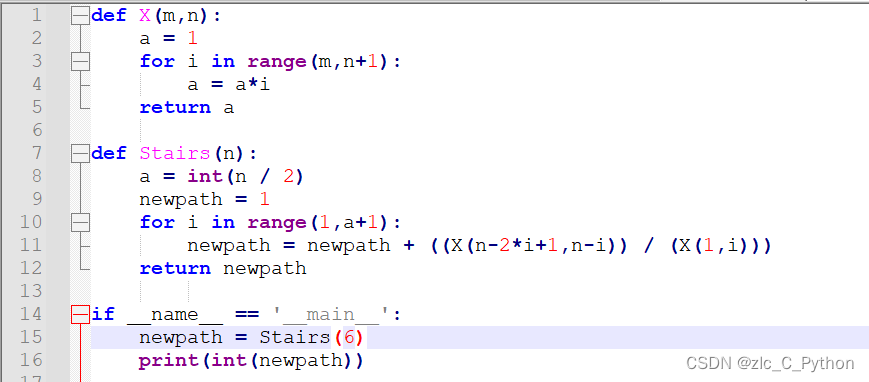
解决代码：

def X(m,n):
    a = 1
    for i in range(m,n+1):
        a = a*i
    return a
        
def Stairs(n):
    a = int(n / 2)
    newpath = 1
    for i in range(1,a+1):
        newpath = newpath + ((X(n-2*i+1,n-i)) / (X(1,i)))
    return newpath
            
if __name__ == '__main__':
    newpath = Stairs(6)
    print(int(newpath))
    

 

---

 项目场景二：

• 一条包含字母 A-Z 的消息通过以下映射进行了 编码 ：
• ‘A’ -> 1’B’ -> 2…‘Z’ -> 26
• 要 解码 已编码的消息，所有数字必须基于上述映射的方法，反向映射回字母（可能有多种方法）。例如，“11106” 可以映射为：
• “AAJF” ，将消息分组为 (1 1 10 6)
• “KJF” ，将消息分组为 (11 10 6)
• 注意，消息不能分组为 (1 11 06) ，因为 “06” 不能映射为 “F” ，这是由于 “6” 和 “06” 在映射中并不等价。
• 给你一个只含数字的 非空 字符串 s ，请计算并返回 解码 方法的 总数 。
• 题目数据保证答案肯定是一个 32 位 的整数。

---

问题描述

• 输入：s = “12”
• 输出：2
• 解释：它可以解码为 “AB”（1 2）或者 “L”（12）。

---

示例分析：

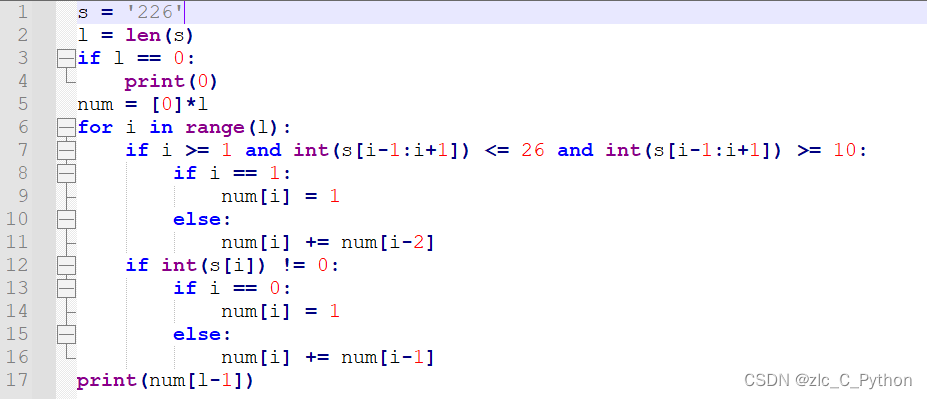
• 输入：s = “226”
• 输出：3
• 解释：它可以解码为 “BZ” (2 26), “VF” (22 6), 或者 “BBF” (2 2 6) 。

---

解决代码：

s = '226'
l = len(s)
if l == 0:
    print(0)
num = [0]*l
for i in range(l):
    if i >= 1 and int(s[i-1:i+1]) <= 26 and int(s[i-1:i+1]) >= 10:
        if i == 1:
            num[i] = 1
        else:
            num[i] += num[i-2]
    if int(s[i]) != 0:
        if i == 0:
            num[i] = 1
        else:
            num[i] += num[i-1]
print(num[l-1])