一

1.类型
有监督：分类、回归
无监督：聚类、降维
2.挑战：
过拟合：泛化能力弱
欠拟合：模型过于简单

二、

1.开发流程
数据收集->数据清洗->特征工程->数据建模
2.选择性能指标：
回归问题 均方根误差rmse

平均绝对误差 mae

rmse 对异常值更加敏感
3.寻找相关性
区间是-1 到 1，靠近0为没有线性相关性
4.数据清理
处理缺失值
5.处理文本和分类属性
将文本转到数字；
有序类别：“坏”“好”“平均”等
无序类别：创建独热向量
6.特征缩放
目标值不缩放，同比例缩放所有属性的两种常用方法是最大最小缩放（归一化）和标准化
7.归一
将值重新缩放使其最终范围在0~1间
实现方法是将值减去最小值并除以最大值和最小值的差
提供转化器
8.标准
首先减去平均值（所以标准化值的均值总是零），然后除以方差，从而使得结果的分布具备单位方差。
标准化不将数值绑定到特定范围。
受异常值影响更小
9.k-折交叉验证
防止过拟合，在训练数据中分出一部分作为验证数据
它将训练集随机分割成k个不同的子集，每个子集称为一个折叠，然后对模型进行k次训练和评估——每次挑选1个折叠进行评估，使用另外的k-1个折叠进行训练。产生的结果是k次评估分数

三、

1.混淆矩阵
行表示实际类别，列表示预测类别

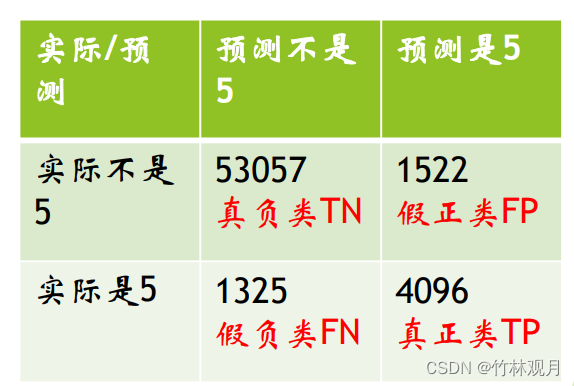
2.精度与召回率

预测与实际相符就是真
预测正面为正

正类预测的准确率是精度：真正占正类的概率
正确检测到的正类实例的比率是召回率：

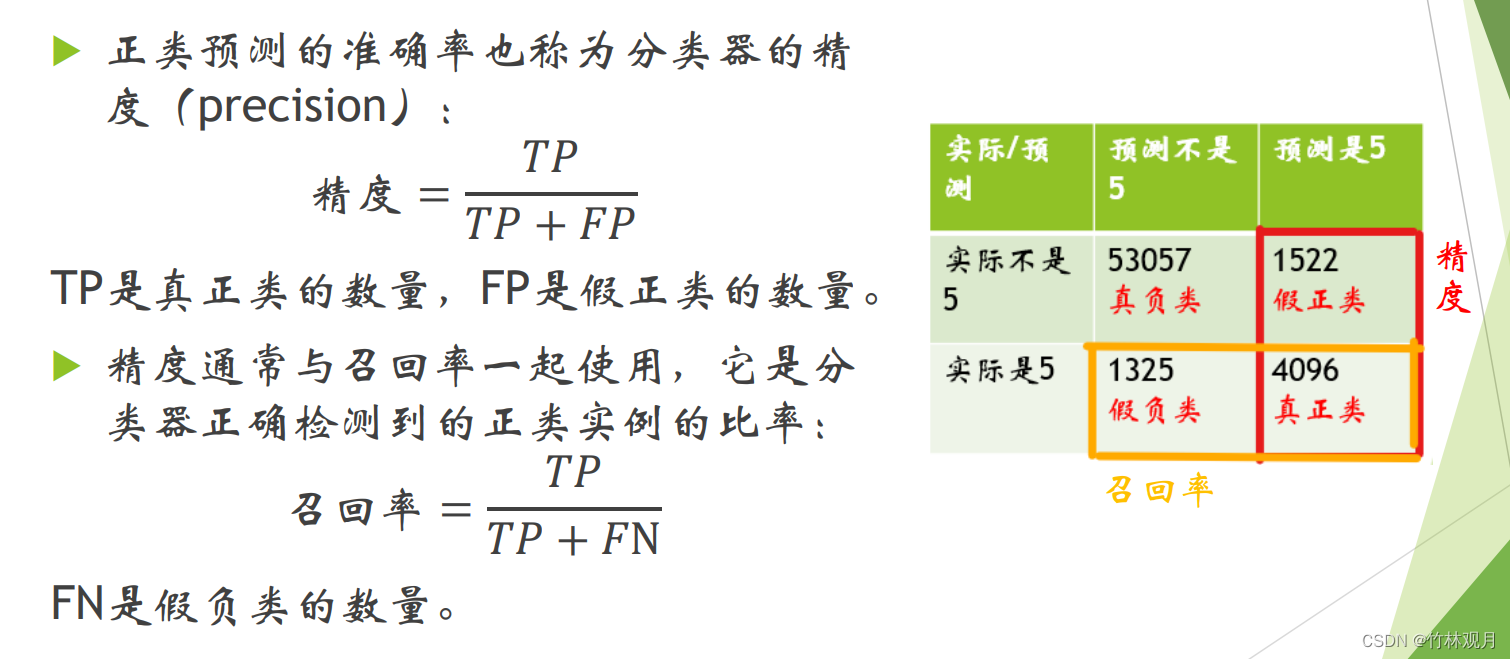
	预测不是	预测是
实际不是	真负	假正
实际是	假负	真正

3.F1分数
$$F_1=\frac{2}{\frac{1}{精度}+\frac{1}{召回率}}$$
F1分数是精度和召回率的谐波（harmonic mean）平均值。
正常的平均值平等对待所有的值，而谐波平均值会给予低值更高的权重。因此，只有当召回率和精度都很高时，分类器才能得到较高的F1分数
4.精度/召回率权衡
基于决策函数计算出一个分值，高于他为正

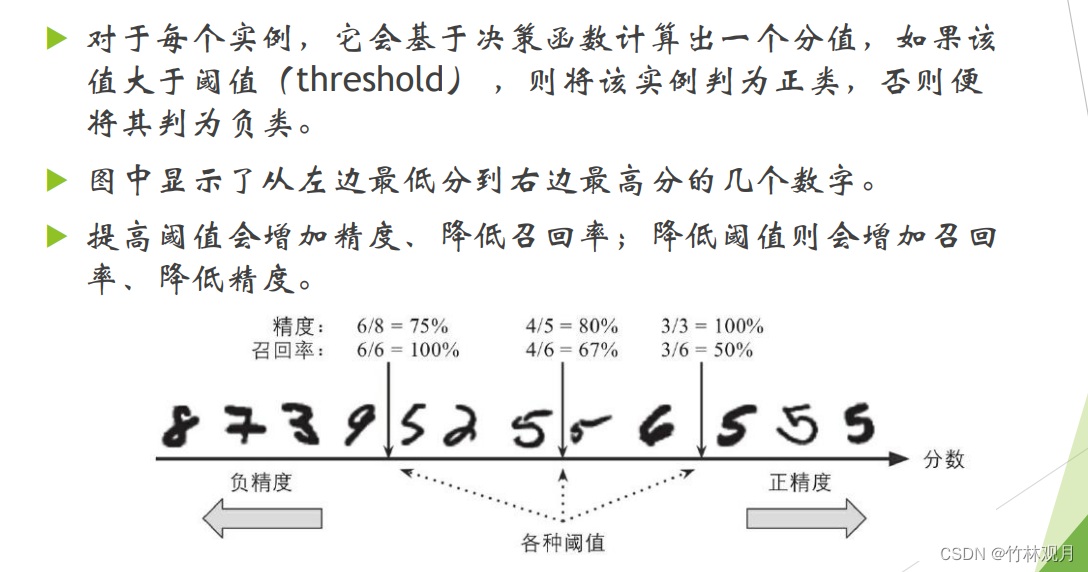
5.roc曲线
绘制的真正类率和假正类率
虚线表示春随机分类器的ROC曲线、优秀的分类器应该远离该曲线（向左上角）
比较方法：测量曲线下面积(AUC)完美的分类器ROC AUC 等于1，纯随机等于0.5

四、

1.梯度下降
优化算法，能够为大范围的问题找到最优解。中心思想：迭代地调整参数从而是成本函数最小化。
调整参数向量相关的误差函数的局部梯度，并不断沿着降低梯度的方向调整直到梯度降为零，达到最小值。
先使用一个随机的θ，然后逐步改进，知道收敛出一个最小值

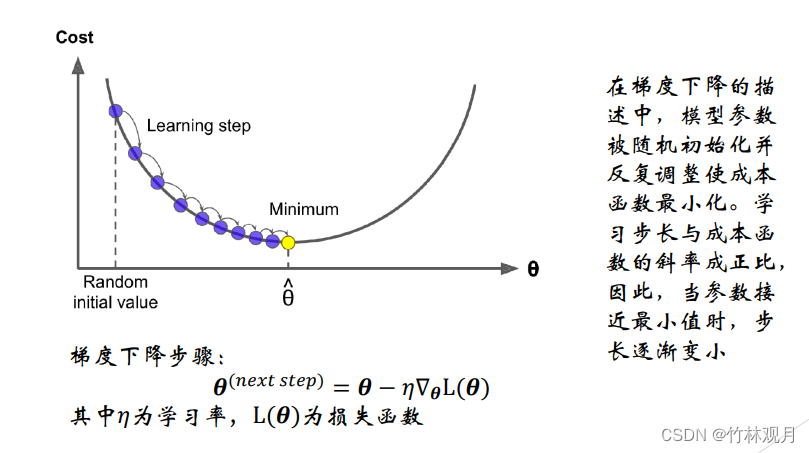
学习率太高太低

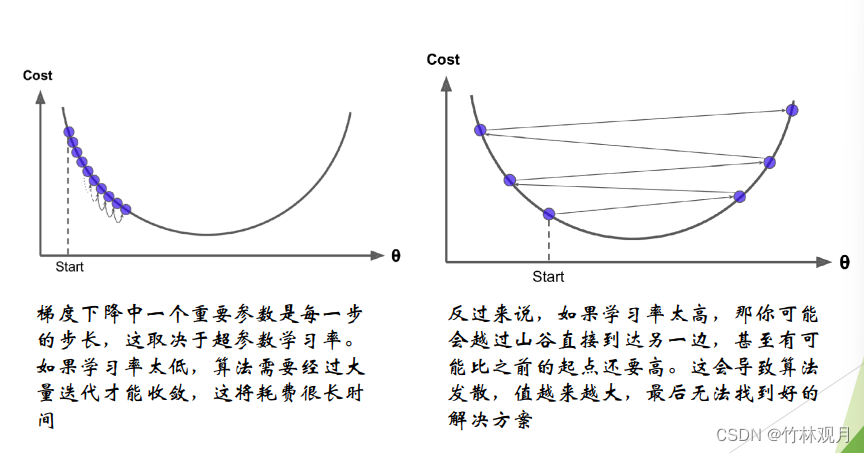
应用梯度下降时，需要保证所有特征值的大小比例都差不多
2.随机梯度下降
随机性的好处在于可以逃离局部最优，缺点是定位不出最小值。
解决方法：逐步降低学习率。开始的步长大然后越来越小。叫做：模拟退火
确定每个迭代学习率的函数叫作学习率调度。
学习率降的太快：可能会陷入局部最小值，甚至是停留在走向最小值的半途中。
太慢：需要太长时间才能跳到差不多最小值附近，如果提早结束训练，可能只得到一个次优的解决方案
3.多项式回归
可以使用线性模型来拟合非线性数据，一个简单的方法就是将每个特征的幂次方添加为一个新特征，然后在此扩展特征集上训练一个线性模型

4.学习曲线
用来估计模型的泛化性能：该曲线绘制的是模型在训练集和验证集上关于训练集大小（或训练迭代）的性能函数
要生成这个曲线，只需要在不同大小的训练子集上多次训练模型即可
5.代码实现
当训练集中只有一个或两个实例时，模型可以很好地拟合它们。随着将新实例添加到训练集中，模型不可能完美拟合。因为有噪声和他不是线性的，训练数据上的误差会一直上升到平稳的状态。
训练模型时，无法正确泛化，最初验证误差很大，经历更多的训练示例，开始学习，验证错误逐渐降低。误差最终达
到一个平稳的状态，非常接近另外一条曲线
与线性回归模型相比，训练时据上的误差会小很多。
曲线之间存在间隙。这意味着该模型在训练数据上的性能要比在验证数据上的性能好得多，这是过拟合模型的标志。如果使用更大的训练集，则两条曲线会继续接近
6.正则化线性模型
减少过拟合的一个好方法是对模型进行正则化（即约束模型）：它拥有的自由度越少，则过拟合数据的难度就越大。
包括岭回归，Lasso回归，弹性网络
7.岭回归
成本函数：

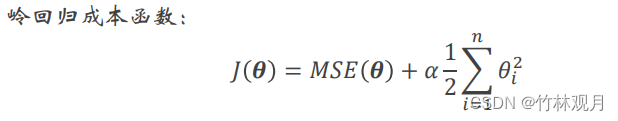
将正则化项添加到成本函数，迫使学习算法不仅拟合数据，而且还使模型权重尽可能小
超参数α控制要对模型进行正则化的程度。如果α=0，则岭回归仅是线性回归。如果α非常大，则所有权重最终都非常接近于零，结果是一条经过数据均值的平线
偏置项𝜃0没有进行正则化
在执行岭回归之前缩放数据（例如使用StandardScaler）很重要，因为它对输入特征的缩放敏感。大多数正则化模型都需要如此
8.Lasso回归

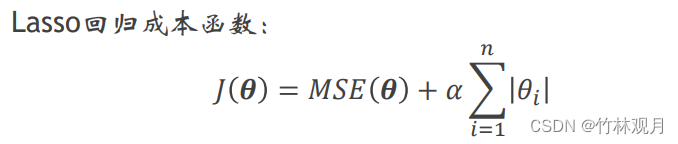
线性回归的另一种正则化叫作最小绝对收缩和选择算子回归
Lasso回归的一个重要特点是它倾向于完全消除掉最不重要特征的权重

7.逻辑回归
被广泛用于估算一个实例属于某个特定类别的概率，是一个二元分类器。
模型：

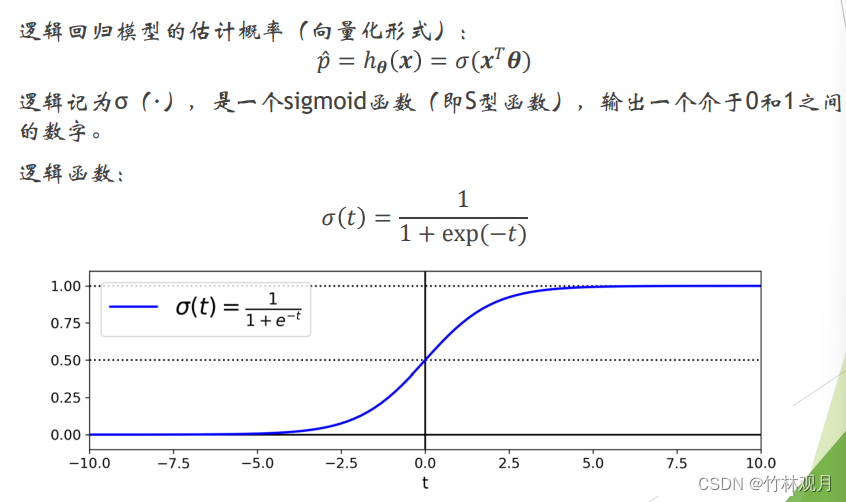
说出介于0和1之间
预测：
估算出实例x属于正类的概率𝑝= ℎ𝜽(𝒙)，就可以做出预测𝑦

8.Softmax回归
经过推广，可以支持多个类别，且不需要训练并组合多个二元分类器
给定一个实例x，Softmax回归模型首先计算出每个类k的分数𝑠𝑘(𝑥)，然后对这些分数应用softmax函数（也叫归一化指数），估算出每个类的概率

五、

1.硬间隔支持向量机

2.非线性支持向量机

六、

决策树模型
1.分类树、回归树
2.基本思想：减少不缺定性
3.度量不确定性的指标：
分类错误率
熵：

基尼指数：

4.结束划分：
预设或无法再分

七、

1.bagging
给定一个训练集，基于自助采样法采样出T个含有m个训练样本的采样集；
基于采样机训练一个基学习器，将这些基学习器进行结合；
每个预测器使用费的算法相同，当时在不同的训练集随机子集上进行训练

2.boosting
增加前一个基学习器在训练过程中预测错误样本的权重，使得后续基学习器更加关注这些打标错误的训练样本，尽可能纠正这些错误，一直向下串行直至产生需要的T个基学习器，Boosting最终对这T个学习器进行加权结合，产生集成学习器。
特点：串行 序列化
3.区别
样本选择：
bagging：训练集在原始集是有放回选取的
boosting：每一轮的训练集不变，只是每个样例的权重发生变化
样例权重：
bagging：权重相等
boosting：根据失误率不服按调整样例的权值，错误率越大权重越大
预测函数：
bagging：所有预测函数的权重相等
boosting：每个弱分类器都有对应的权重，对于分类误差小的分类器权重更大
并行计算：
bagging：可以并行
boosting：只能顺序生成

九、

1.主成分分析
需要找到一种合理的方法，在减少需要分析的指标同时，尽量减少原指标包含信息的损失，以达到对所收集数据进行全面分析的目的。
由于各变量之间存在一定的相关关系，因此可以考虑将关系紧密的变量变成尽可能少的新变量，使这些新变量是两两不相关的，那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。
降维算法
2.概念
PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。
PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。
第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。
通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。
于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。
3.基于特征值分解协方差矩阵实现PCA算法