常见的六大聚类算法
https://blog.csdn.net/m0_57656758/article/details/127653402?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522167669020916782425666238%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=167669020916782425666238&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-3-127653402-null-null.blog_rank_default&utm_term=聚类&spm=1018.2226.3001.4450

PAM算法基本思想

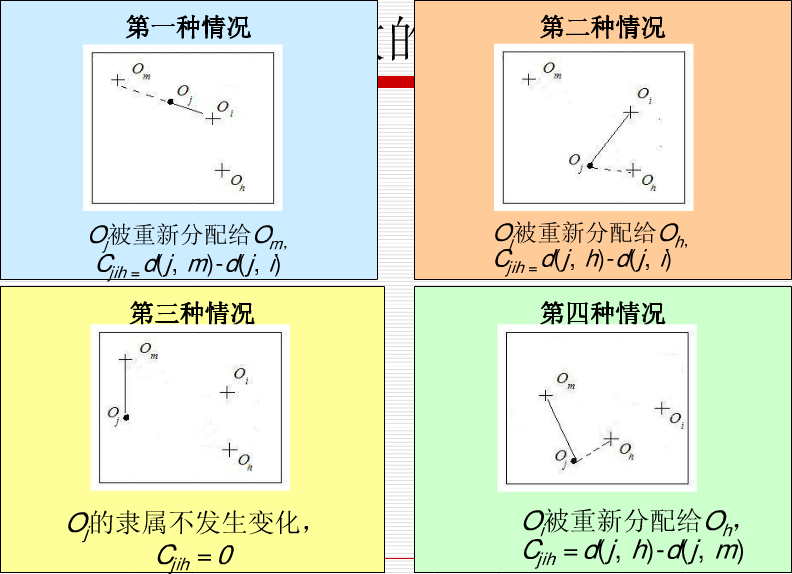
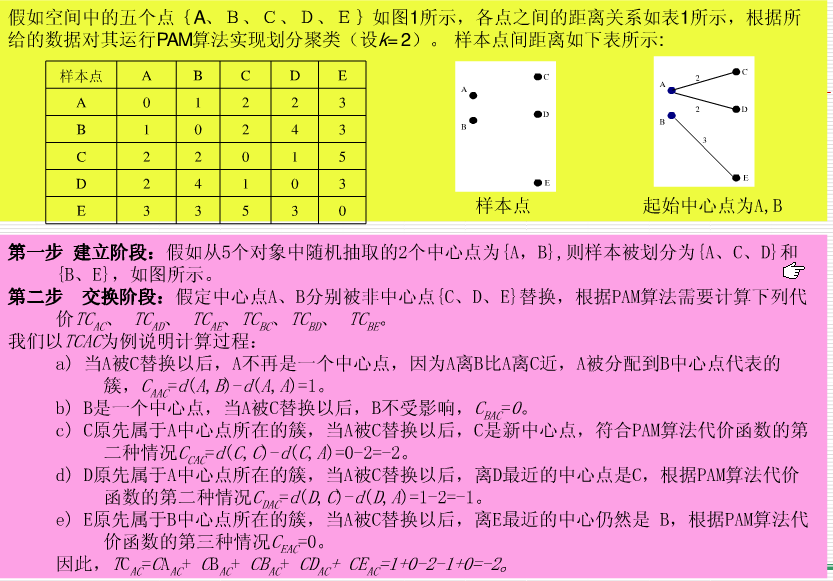
PAM作为最早提出的k-中心点算法之一，它选用簇中位置最中心的对象作为代表对象，试图对n个对象给出k个划分。

代表对象也被称为是中心点，其他对象则被称为非代表对象。

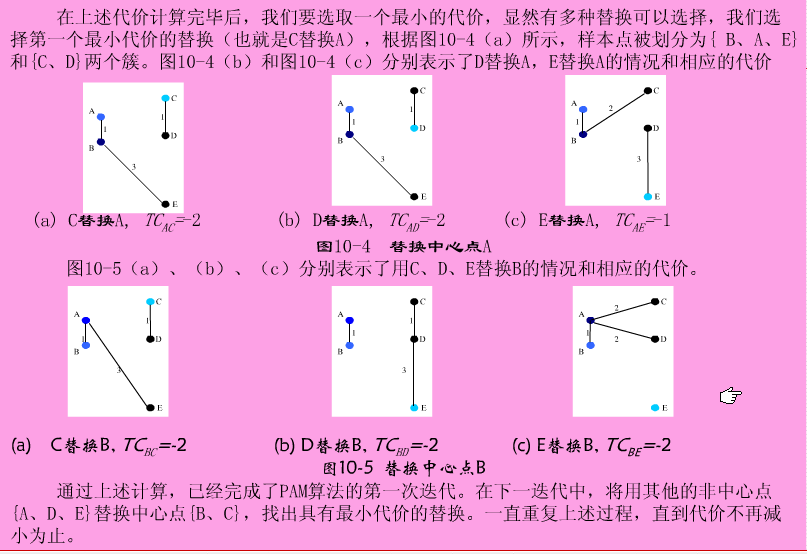
最初随机选择k个对象作为中心点，该算法反复地用非代表对象来代替代表对象，试图找出更好的中心点，以改进聚类的质量。

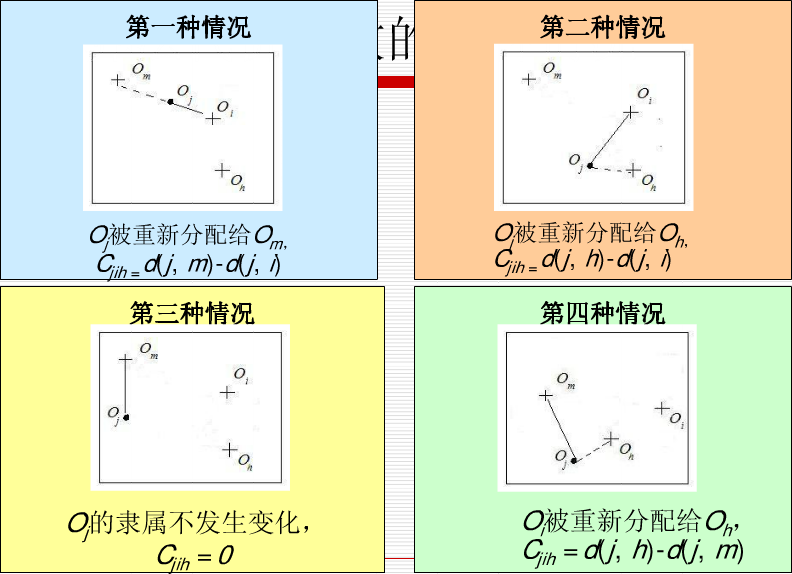
在每次迭代中，所有可能的对象对被分析，每个对中的一个对象是中心点，而另一个是非代表对象。

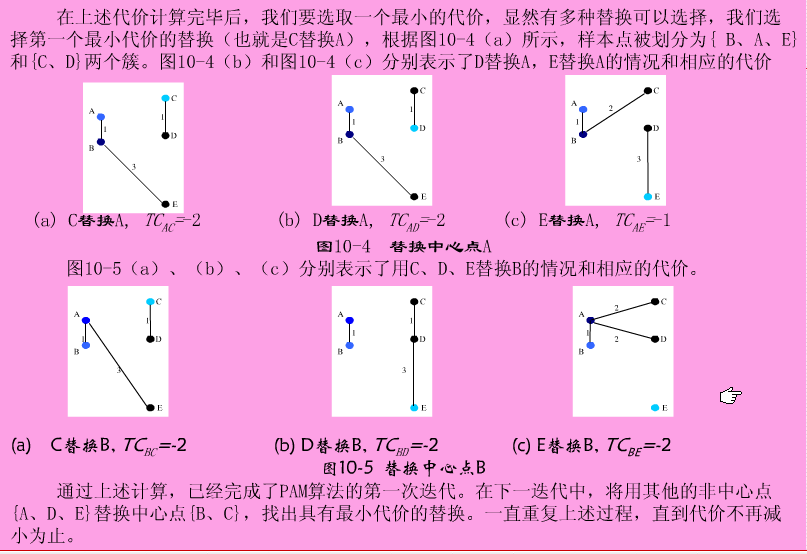
对可能的各种组合，估算聚类结果的质量。一个对象Oi被可以产生最大平方-误差值减少的对象代替。在一次迭代中产生的最佳对象集合成为下次迭代的中心点。

常用来肠型分析

bilibili视频网址： https://www.bilibili.com/video/BV1KF411E7XV/?spm_id_from=333.337.search-card.all.click&vd_source=deb12d86dce7e419744a73045bc66364

无监督聚类PAM（中心法划分）和DMM（狄利克雷多项混合模型）是两种重要机器学习无监督聚类算法，应用肠道微生物分型和代谢组聚类等。

目前流行的肠型分析计算方法有2种：一种是基于样品间的Jensen-Shannon距离，利用围绕中心点划分算法(PAM)进行聚类，最佳分类数目通过Calinski-Harabasz(CH)等指标确定；另一种是直接基于物种丰度，利用狄利克雷多项混合模型(DMM)进行肠型分析，基于最低的拉普拉斯近似分数(laplace)来确定合适的聚类数。

CH指标

导入肠道微生物分布数据，CH指标(Calinski-Harabas)通过计算类中各点与类中心的距离平方和来度量类内的紧密度，CH越大代表着类自身越紧密，CH小即代表类与类之间越分散，存在更优的聚类结果。

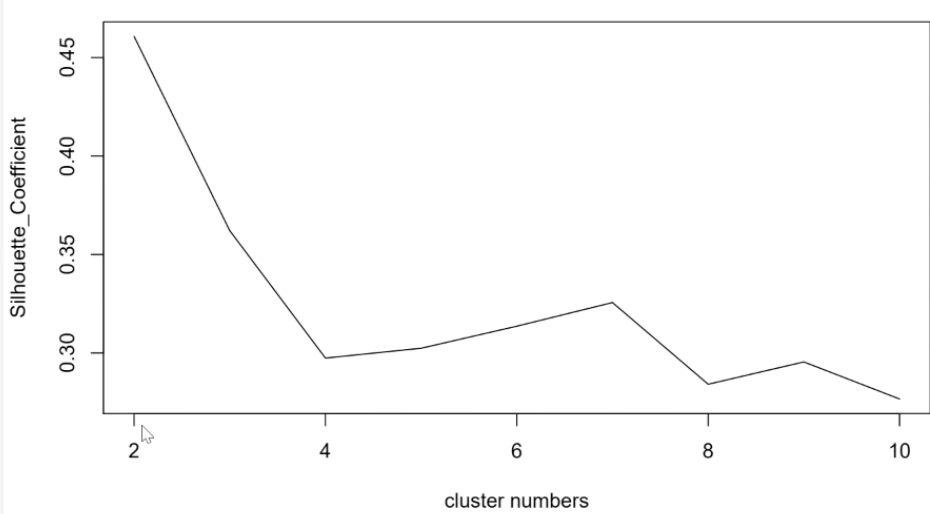
轮廓系数

轮廓系数(Silhouette Cofficient)是聚类效果好坏的一种评价方式，值越大，聚类效果越好。 

拉普拉斯近似分数

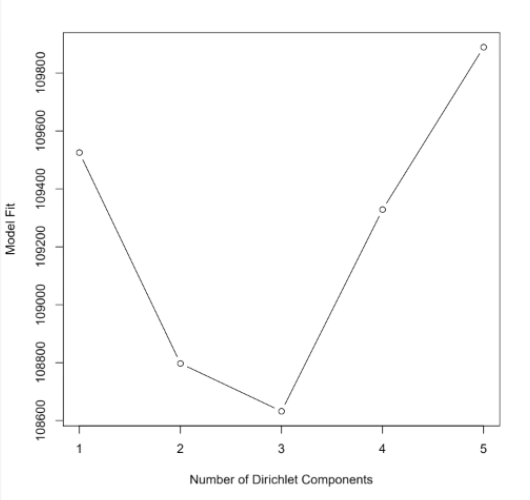
k clusters

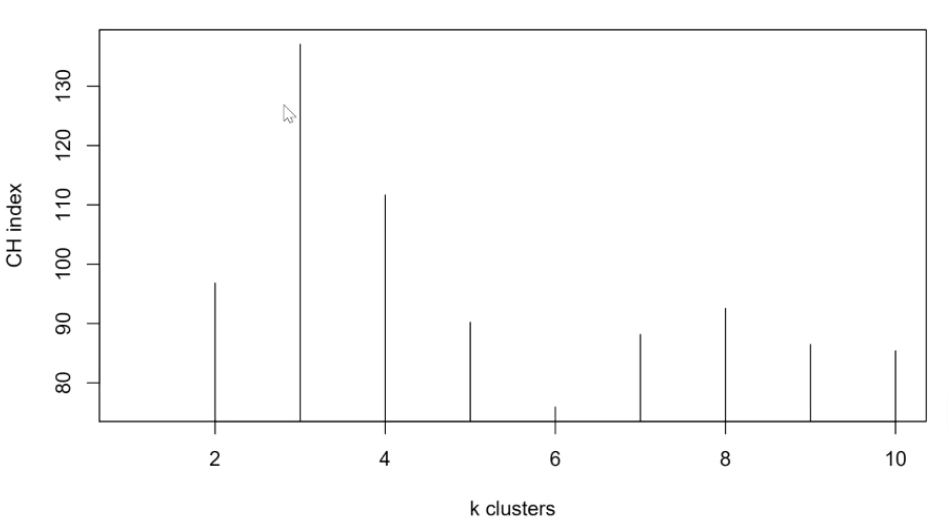
k=3，聚类效果最好。

https://blog.csdn.net/zd200572/article/details/85338360?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522167668849716800222823119%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=167668849716800222823119&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~rank_v31_ecpm-2-85338360-null-null.142^v73^insert_down3,201^v4^add_ask,239^v2^insert_chatgpt&utm_term=肠型分析PAM&spm=1018.2226.3001.4187