👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 文献来源
🌈4 Matlab代码实现
💥1 概述
本文为可再生能源渗透率高的联合电力和天然气系统的能源和储备调度制定了两阶段随机程序。数据驱动的分布式鲁棒机会约束确保了不存在高概率的甩负荷和可再生溢出。我们使用条件风险值近似和线性决策规则有效地解决了这个问题。样本外实验表明,该模型在没有机会约束的情况下主导了相应的随机程序,该程序明确地模拟了甩负荷和可再生能源溢出的影响。
风能、太阳能和潮汐能等可再生能源的增加部署极大地改变了发电结构。可再生能源虽然有利于可持续发展,但由于其间歇性和有限的可预测性,会损害输电系统的稳定性[27]。因此,广泛建造柔性燃气发电厂(GFPP),以取代退役的热电厂或核电站,以平衡不稳定的可再生能源发电,因此,电力和天然气系统的紧密耦合是可以预见的[28]。这种观点促使我们同时研究这两个系统在存在不确定的可再生能源的情况下,如果实际的可再生能源产量与其预测值不符,则日前调度可能无法实施。在这种情况下,传统发电厂需要实时调整其生产水平。如果在某些极端情况下,这些发电厂不够灵活,无法恢复输电系统的完整性,那么可再生能源泄漏或甩负荷可能变得必要。然而,这种激烈的措施带来了高昂的经济成本。
能源和储备调度问题可以通过鲁棒优化[3]、随机规划[26]和机会约束规划[24]的方法来解决。稳健的优化模型最大限度地降低了日前调度的成本,以及在规定的不确定性集合内最坏情况下实现可再生预测误差的纠正补救措施[4,35]。然而,对最坏情况的关注以及在线性决策规则中解决更大问题实例的必要性可能会导致过于保守的解决方案
另一方面,随机规划模型在规定的离散分布下使预期成本最小化[21,23],但除非离散点的数量随问题维度呈指数增长,否则其解决方案可能表现出较差的样本外性能。最后,机会约束规划模型不考虑可再生能源泄漏和甩负荷,但确保在没有这些严重的补救措施的情况下,系统保持高概率稳定[5,18,25]。当难以或甚至不可能以有意义的方式将追索权和不可行性货币化时,机会受限的编程公式尤其具有吸引力。不利的是,这些公式通常不能保证产生可行的可实施的第一阶段解决方案。
本文的结果表明,为了最小化样本外成本,解决分布式鲁棒机会约束程序可能比(看起来更现实的)两阶段分布式鲁棒优化问题更好。这可能令人惊讶,因为机会约束计划忽略了所有低概率情况,在这些情况下,电力系统的稳定性只能通过成本高昂的追索行动(如甩负荷和可再生能源泄漏)来维持,而两阶段问题说明了所有可能的情况,并真实地模拟了必要的追索行动及其成本。
📚2 运行结果
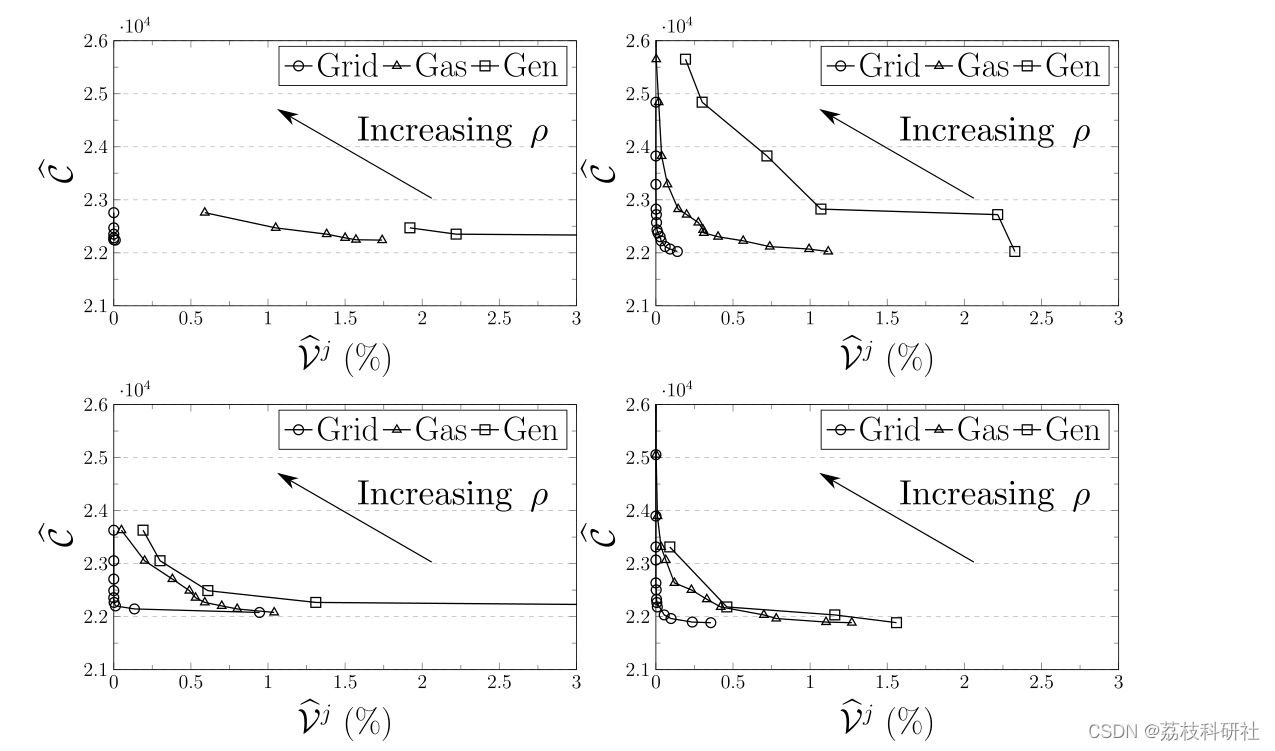
文章运行结果:
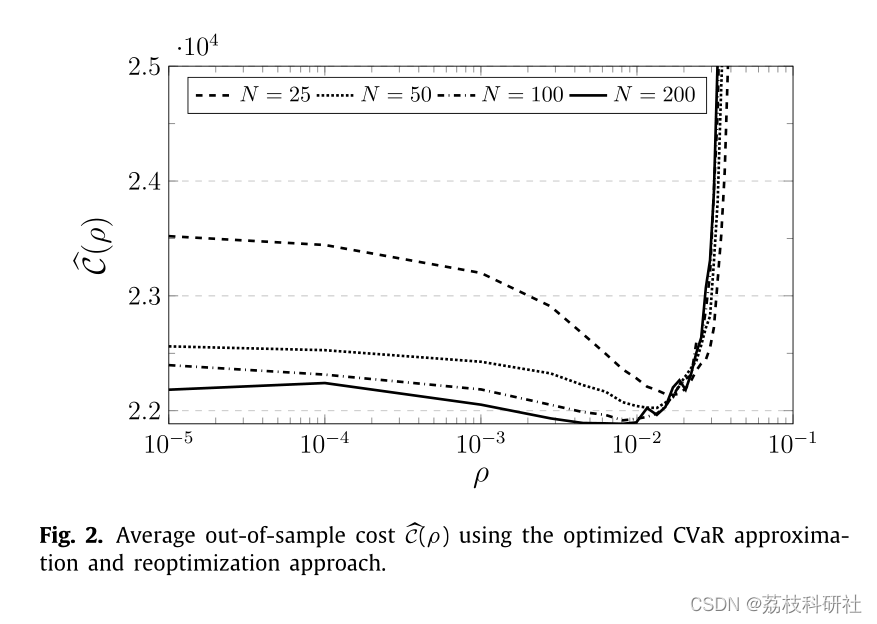
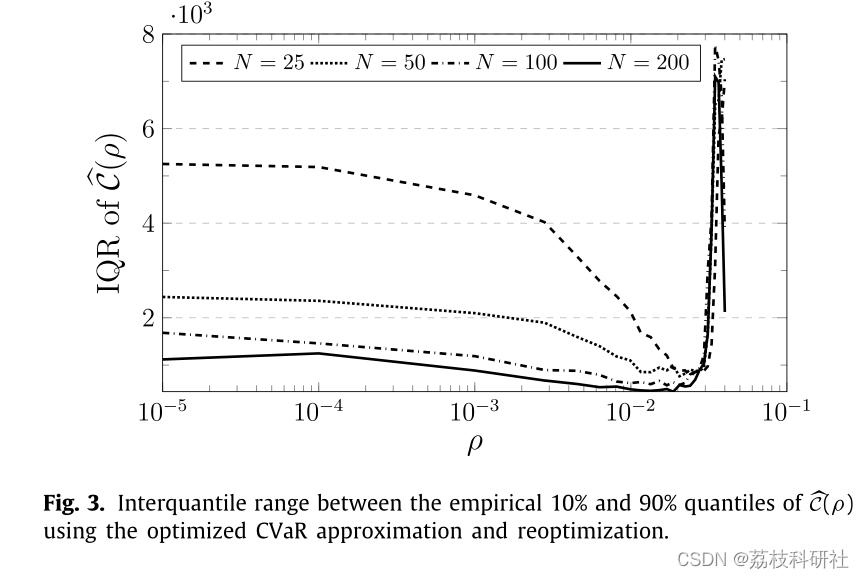
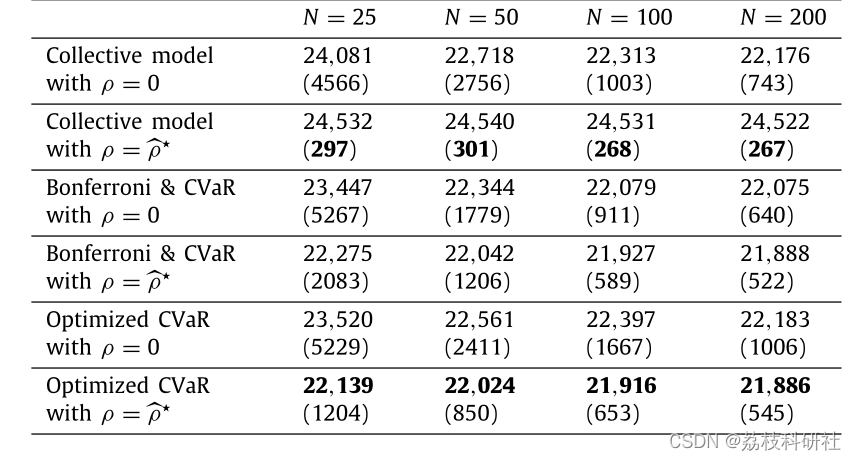
部分代码:
function[sol] = DRO_CVaR_ICC(si,DRO_param,jcc)
% This script implements the Bonferroni approximation
yalmip('clear')
% Getting the number of thermals power plants, wind farms, scenarions,
% transmission lines and nodes
Nunits = size(si.Pmax,1);
Nwind = size(si.Wmax,1);
Nscen = size(si.Wscen,2);
% Definition of variables
p = sdpvar(Nunits, 1); % Day-ahead power production from thermal power plants
ru = sdpvar(Nunits, 1); % Upward reserve dispatch from thermal power plants
rd = sdpvar(Nunits, 1); % Downward reserve dispatch from thermal power plants
Y = sdpvar(Nunits, Nwind, 'full'); % Linear decision rule for real-time power production
s_obj = sdpvar(1, Nscen); % sigma variable for obj
lambda_obj = sdpvar(1, 1); % lambda variable for obj
% create x by stacking up p, ru and rd
x = [p; ru; rd];
% Constraints set
CS = [];
% Day-ahead constraints
CS = [CS, si.Pmin <= p - rd, p + ru <= si.Pmax, 0 <= ru <= si.ResCap, 0 <= rd <= si.ResCap];
CS = [CS, sum(p) + sum(si.Wmax.*si.mu) - sum(si.D) == 0];
CS = [CS, sum(Y, 1) == -si.Wmax'];
% Run a for-loop to add the constraints related to the individual cvar
% The set of code below is generic, it can be copied and paste for any
% structure joint chance constraint of interest
% find the number of Individual chance constraints we have
nICC = 0;
for j=1:size(jcc, 1)
nICC = nICC + size(jcc{j, 1}, 1);
end
for j=1:size(jcc, 1)
A_C{j,1} = jcc{j,1};
B_C{j,1} = jcc{j,2};
C_C{j,1} = jcc{j,3};
b_C{j,1} = jcc{j,4};
end
A = cell2mat(A_C);
B = cell2mat(B_C);
C = cell2mat(C_C);
b = cell2mat(b_C);
for j=1:size(jcc, 1)
eps_C(j) = jcc{j,5}/size(jcc{j, 1}, 1);
end
eps = [repmat(eps_C(1),size(jcc{1, 1}, 1),1);repmat(eps_C(2),size(jcc{2, 1}, 1),1);repmat(eps_C(3),size(jcc{3, 1}, 1),1)];
% create variables
s = sdpvar(nICC, Nscen, 'full');
lambda = sdpvar(nICC, 1);
tau = sdpvar(nICC, 1);
for j = 1:nICC
CS = [CS, DRO_param.rho*lambda(j) + sum(s(j, :))/Nscen <= 0];
CS = [CS, tau(j) <= s(j,:)];
CS = [CS, (1 - 1/eps(j))*repmat(tau(j), 1, Nscen) + 1/eps(j)*( repmat(A(j,:)*x - b(j), 1, Nscen) + (B(j,:)*Y+C(j,:))*si.xi ) <= s(j,:) ];
CS = [CS, norm(1/eps(j)*(B(j,:)*Y + C(j,:)), DRO_param.dual_norm) <= lambda(j)];
end
% Build the objective function
Obj = si.Cr1'*ru + si.Cr2'*rd + si.C'*p + DRO_param.rho*lambda_obj + 1/Nscen * sum(s_obj);
CS = [CS, si.C'*Y*si.xi <= s_obj];
CS = [CS, norm( Y' * si.C, DRO_param.dual_norm) <= lambda_obj];
% Settings
optim_options = sdpsettings('solver', 'gurobi','gurobi.TimeLimit',1000,'gurobi.NumericFocus',3,'verbose',0);
% Solve
sol = optimize(CS, Obj, optim_options);
sol.p = value(p);
sol.Y = value(Y);
sol.ru = value(ru);
sol.rd = value(rd);
sol.Y = value(Y);
sol.fy = si.Qg*value(p) + si.Qw*si.DiagWmax * si.mu - si.Qd*si.D;
sol.fY = si.Qg*value(Y) + si.Qw*si.DiagWmax;
sol.q = si.PG * value(p);
sol.qY = si.PG * value(Y);
sol.Obj = value(Obj);
sol.Flag = sol.problem;
end
🎉3 文献来源
部分理论来源于网络,如有侵权请联系删除。