强化学习是一种机器学习方法，通过agent与environment的互动，学习适当的action policy以取得更大的奖励reward。本篇博客介绍强化学习的基础知识，与两类强化学习模型。

强化学习的基础设定

强化学习和监督学习，非监督学习一样是一种基本学习模式，在强化学习的框架中，一共有2个主体：agent与environment。environment会给agent一些状态信息state，agent可以根据state的情况进行action的选择，并从environment获得一些奖励reward。

强化学习分为2类：policy based和value based。二者并非互斥关系，存在一些模型既是policy based又是value based 例如：A3C[ICML2016]。

policy based 强化学习的目标

强化学习的目标是学习一个policy使得最终全场决策下来得到的总reward最大。具体展开而言，给定一个state，agent决策采取action的策略模型，用$\pi$表示，$\pi$的参数是$\theta$，由于policy根据state采取action，我们可以用公式：$a={\pi }_{\theta }(s)$表示。当agent做出action操作后，environment会给出一个reward并更新状态，至此一轮决策结束。多轮决策组成一个由state, action, reward组成的序列，我们定义为$\tau =(s_1,a_1,r_1,...s_T,a_T,r_T)$。$R_{\tau }$是整场决策结束后总共的奖励，$R_{\tau }={\sum }_{t=1}^T{r}_t$，强化学习的目的是最大化$R_{\tau }$。

在实际决策过程中，即便$\pi$和environment不变，每一步的action依旧有随机性，因而最终的奖励$R_{\tau }$也不会完全一致，而是具有一些随机性。因此强化学习的目标为最大化一个$\pi$下的平均$R_{\tau }$，即$E[R_{\tau }]={\sum }_{\tau }R(\tau )p(\tau |\theta )$，很显然我们无法得到准确的期望，因为我们无法把一个参数设定下所有的决策路径全都取一个遍，因而实际使用中，通过采样取平均值的方法得到一个期望的近似值。$R(\theta )\approx \frac{1}{N}{\sum }_{n=1}^{N}R({\tau }_n)$。

强化学习的优化目标即为：$R(\theta )\approx \frac{1}{N}{\sum }_{n=1}^{N}R({\tau }_n)$。

通过梯度下降提升优化目标，这一步需要求$R(\theta )$的导数。$$\begin{gathered} \nabla R_{\theta }=\sum _{\tau }R(\tau )\nabla p(\tau |\theta )=\sum _{\tau }R(\tau )p(\tau |\theta )\frac{\nabla p(\tau |\theta )}{p(\tau |\theta )}=\sum _{\tau }R(\tau )p(\tau |\theta )\nabla log(p(\tau |\theta )) \\ p(\tau |\theta )=p(s_1)p(a_1|s_1)p(s_2,r_1|s_1,a_1)...p(s_T,r_{T-1}|s_{T-1},a_T) \\ log(p(\tau |\theta ))=log(p(s_1))+\sum _{t=1}^{T}log(p(a_t|s_t,\theta ))+\sum _{t=1}^{T}log(p(r_t,s_{t-1}|s_t,a_t)) \\ \nabla log(p(\tau |\theta ))=\sum _{t=1}^T\nabla log(p(a_t|s_t,\theta )) \end{gathered}$$
最终得到$\nabla R_{\theta }$的表达式:$\nabla R_{\theta }\approx \frac{1}{N}{\sum }_{n=1}^N{\sum }_{t=1}^{T}R({\tau }_n)\nabla log(p(a_t|s_t,\theta ))$ (*)

3个注意事项

1. 为什么要构成log的形式：进行归一化，降低采样偶然性对于低reward但高频对梯度的影响
2. 由于采样具有偶然性，考虑到不被采样到的点以及$R(\tau )$有时候可能一直取正数，将公式里的$R(\tau )$替换为$R(\tau )-b$进行修正
3. (*)给每个梯度的权重只考虑了整场决策的reward，忽略了每个action的独特性，对其进行改进，我们引入advantage function：$A^{\theta }(s_t,a_t)$用于衡量$s_t$状态下采用$a_t$相对于其他action有多好的程度。

实际训练过程

给定初始化的参数${\theta }_0$，采样$N$个$\tau$计算每个$\tau$的reward,计算当前参数下的$\nabla log(p(a_t|s_t,\theta ))$，进行参数$\theta$的梯度更新得到${\theta }_1$，然后对新得到的参数进行下一轮的采样与梯度更新直至训练停止。

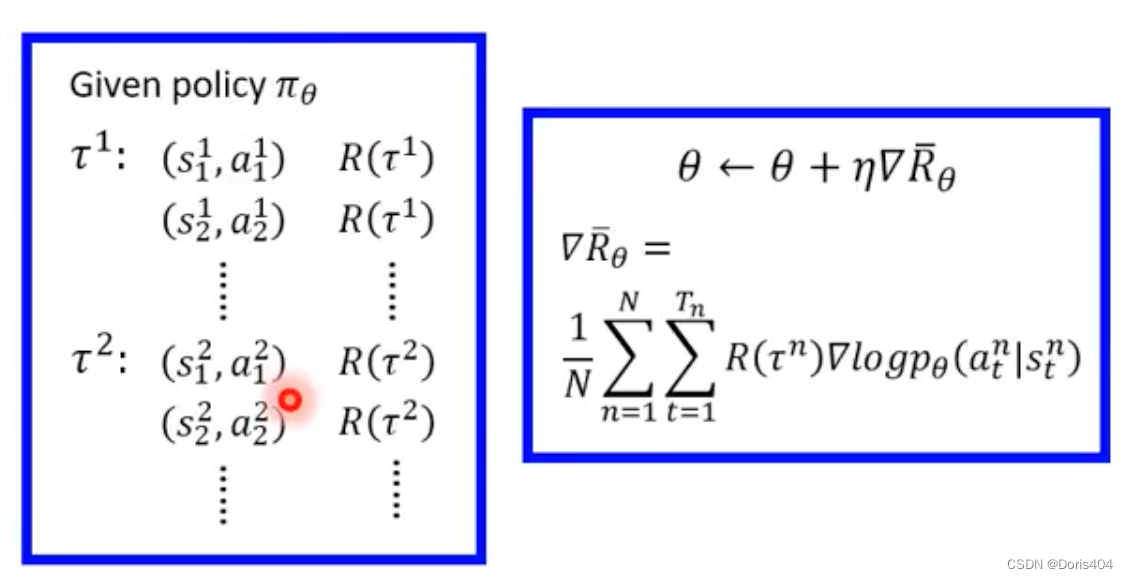
这种训练方法被有一个问题：每次更新参数都需要重新采样，消耗了大量的时间。因而提出了off policy的方法减少采样带来的时间开销。

重要性采样

重要性采样（importance sampling）方法可以减小采样的个数，极大地提升了采样的效率。其具体实现如下：假定我们有一个分布$p$，我们从分布$p$中进行采样得到$x$，我们希望计算得到函数$f(x)$的期望值，即$E_{x\sim p}[f(x)]$。一个直观的思路是我们先根据分布$p$采样$N$个点，然后计算这$N$个点的均值作为期望的估计。然而有时候我们无法直接从分布$p$进行采样，这种时候可以从一个与分布$p$接近的分布$q$进行采样，然后将结果转化为依据分布$p$采样的均值。
$$E_{x\sim p}[f(x)]=E_{x\sim q}[f(x)\frac{p(x)}{q(x)}]$$这里的分布$q$应该尽可能接近分布$p$时，公式才能在采样意义下成立。

off policy的方法使用重要性采样的方法降低了采样的次数进而减小了采样带来的时间开销。on policy方法与off policy方法最大的区别就是二者采样的方式是不同的，on policy方法使用梯度下降方法更新参数后按照新参数进行采样，而off policy方法依旧使用之前旧参数采样的结果（这里假设了参数更新并未很多因而分布变化并不大）。

on policy：$\nabla R_{\theta }=E_{\tau \sim p_{\theta }(\tau )}[R({\tau }_n)\nabla log(p_{\theta }(\tau ))]$
off policy：$\nabla R_{\theta }=E_{\tau \sim p_{{\theta }^{\prime }}(\tau )}[R({\tau }_n)\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}\nabla log(p_{\theta }(\tau ))]$

可以发现off policy在参数设定为${\theta }^{\prime }$下进行采样，梯度下降更新的是$\theta$而非${\theta }^{\prime }$，因此采样可以复用。

value based 强化学习的目标

与policy based强化学习不同，value based模型通过神经网络学习environment针对给定state以及action的reward，帮助agent进行当前state进行action的决策。value based强化学习假定存在一个类似于先知的函数$Q(s,a;\theta )$它可以在给定state的条件下计算出每个action的奖励期望是多大，并且用一个神经网络来学习它。有了这样的先知后，模型自然可以通过选择当前state下reward最高的action进行操作。

Temporal Differential learning (TD learning)

TD learning是训练上述$Q(s,a;\theta )$模型的方法，其训练思想基于监督学习，需要一个“真实标签”。但由于真实标签在这个训练场景下获取需要大量时间开销，因此我们会用TD target来拟合真实的标签即拟合真实的reward$$y_t=r_t+\max \gamma Q(s_{t+1},a_{t+1};\theta )$$，并使用梯度下降方法来使得$Q(s_t,a_t;\theta )$接近$y_t$。

参考

1. 价值学习__Value-Based_Reinforcement_Learning(ps：这个up也出了视频介绍policy-based reinforcement learning视频不长，讲的很清晰）
2. 李弘毅老师强化学习教学视频合集(ps:里面有一些视频内容是重合的可以挑着看）