题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

如下图所示： 有 9 只盘子，排成 1 个圆圈。 其中 8 只盘子内装着 8 只蚱蜢，有一个是空盘。 我们把这些蚱蜢顺时针编号为 1 ~ 8。

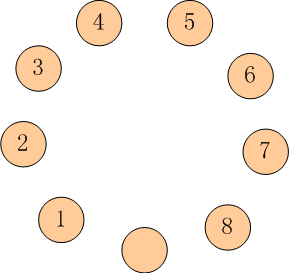
每只蚱蜢都可以跳到相邻的空盘中， 也可以再用点力，越过一个相邻的蚱蜢跳到空盘中。

请你计算一下，如果要使得蚱蜢们的队形改为按照逆时针排列， 并且保持空盘的位置不变（也就是 1−8 换位，2−7换位,...），至少要经过多少次跳跃？

思考：

从起始状态到终止状态，求最少跳跃次数最短路径问题，用BFS

建模

        ·直接让蚱蜢跳到空盘有点麻烦，因为有很多蚱蜢在跳。
        ·反过来看，让空盘跳，跳到蚱蜢的位置，简单多了，只有一个空盘在跳。
化圆为线
        ·题目是一个圆圈，不好处理，用一个建模技巧“化圆为线”，把圆形转换为线形。
        ·把空盘看成0，有9个数字{0,1,2,3,4,5,6,7,8}，一个圆圈上的9个数字，拉直成了一条线上的9个数字，这条线的首尾两个数字处理成相连的。
        ·八数码问题：有9个数字{0,1,2,3，4,5,6,7,8}，共有9！=362880种排列，不算多。

 最短路径

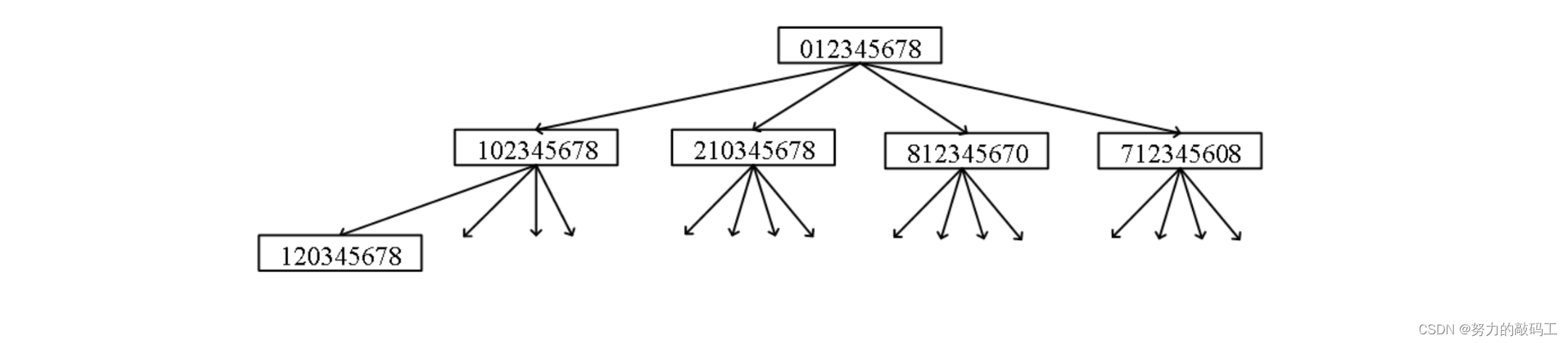
·初始状态：“012345678”，目标状态：“087654321”。·从初始状态“012345678”跳一次，有4种情况：“102345678”“210345678”、“812345670”、“712345608”。
·然后从这4种状态继续跳到下一种状态，一直跳到目标状态为止。

·用BFS扩展每一层。
·每一层就是蚱蜢跳了一次，扩展到某一层时发现终点“087654321”，这一层的深度就是蚱蜢跳跃的次数。

 

 去重

·判重：判断有没有重复跳，如果跳到一个曾经出现过的情况，就不用往下跳了。一共只有9！=362880种情况。
·代码的复杂度：在每一层，能扩展出最少4种、最多362880种情况，最后算出的答案是20层，那么最多算20*362880=7,257,600次。在代码中统计实际的计算次数，是1451452次。
·队列：最多有9！=362880种情况进入队列。

参考代码：

from collections import *
def indeque(q,dir,news,vis):
  pos=news[1]       #空盘子的位置
  status=news[0]
  zb=(pos+dir+9)%9  #处理坐标的方式
  t=list(status)    #将字符串转化为列表，便于理解
  t[pos],t[zb]=t[zb],t[pos]  #互换
  addStatus=''.join(t)   #将新的添加进
  if addStatus not in vis:
    vis.add(addStatus)    #判重
    q.append((addStatus,zb,news[2]+1))

q=deque()
q.append(("012345678",0,0)) #第一个 0 表示空盘子的位置，第二个 0 表示次数
vis=set()
vis.add("012345678")
while q:
  news=q.popleft()
  if news[0]=="087654321": #到达目标状态，输出最少步数
    print(news[2])
    break
  indeque(q,-2,news,vis) #扩展下一层的四种状态
  indeque(q,-1,news,vis)
  indeque(q,2,news,vis)
  indeque(q,1,news,vis) 
#print(20)

---

DFS判重：

 set（）判重：

字典判重：