作者:~小明学编程
文章专栏:Java数据结构
格言:目之所及皆为回忆,心之所想皆为过往
目录
简介
前序遍历
递归法
迭代法
中序遍历
递归法
迭代法
后序遍历
递归法
迭代法
简介
前面学习二叉树的时候,已经学过的二叉树的前中后序的遍历,但是当时实现功能的时候采用的都是递归法,今天把迭代法也说一下,虽然二者的时间复杂度和空间复杂度一样,但是递归可能会导致栈爆了的风险,当然对于我来说这都不是我去学习迭代法的主要原因,毕竟递归法真的太简单明了了,让我学习迭代法的原因是这段评论。
看到了吧,兄弟们,递归法太简单了,面试谁考你递归遍历呀,所以迭代还是很有必要学习学习的,在这里用力扣的代码重新给大家介绍递归法,同时补充迭代法。
前序遍历
链接:144. 二叉树的前序遍历 - 力扣(LeetCode)
递归法
class Solution {
List<Integer> list = new ArrayList<>();
private void preOrder(TreeNode root) {
if (root==null) {
return;
} else {
list.add(root.val);
preOrder(root.left);
preOrder(root.right);
}
}
public List<Integer> preorderTraversal(TreeNode root) {
preOrder(root);
return list;
}
}此时的递归法显得那么的朴实无华,简洁明了,这里我们把打印节点换成了向List中添加元素,思路很简单,我们先添加元素然后preOrder(root.left)调用自己开始递归,直到我们的节点为空节点,此时直接返回然后调用preOrder(root.right)接着进行递归。
迭代法
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> lis = new LinkedList<>();
Stack<TreeNode> stack = new Stack();
while (!stack.isEmpty() || root!=null) {
while (root != null) {
lis.add(root.val);
stack.push(root);
root = root.left;
}
root = stack.pop();
root = root.right;
}
return lis;
}
}迭代法的话就稍微复杂一点了,得用到我们的栈来实现了,先new一个List用于储存我们的数据,然后再new一个栈出来辅助我们来遍历二叉树,因为是先根遍历所以我们只要进了循环直接add向里面添加元素,然后进行压栈操作,将我们的根节点给压进去,然后root==root.left(根完了之后就是左)。
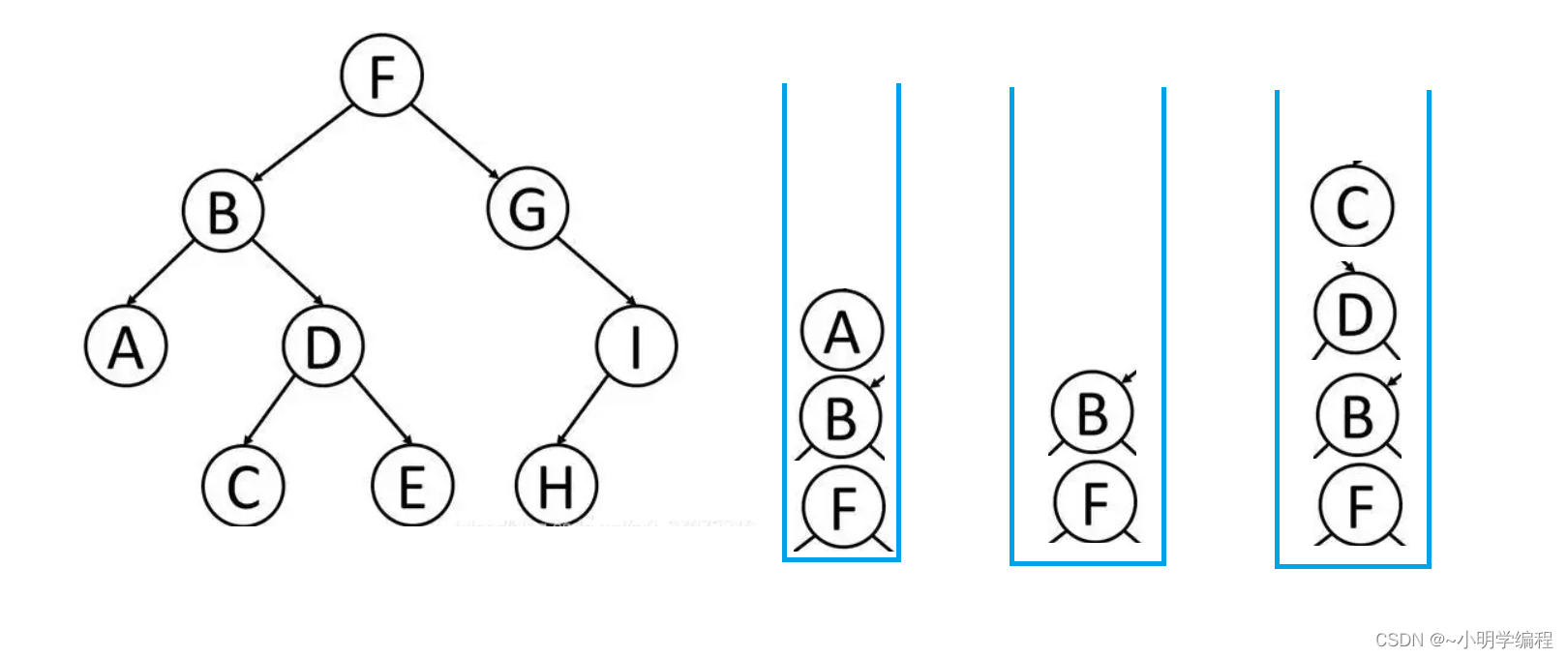
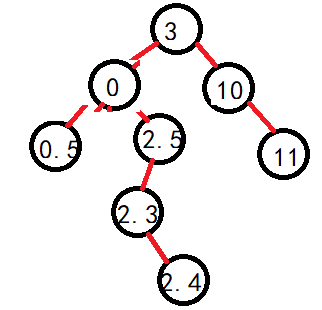
如图接着就是将栈顶元素A给出了,然后就找到A的右,A的右为空所以继续pop()就找到了B,依此类推直到我们的栈为空,但是我们的第一个循环里面加了一个root!= null,这是因为刚开始我们的栈是空的,不然刚开始我们进不去循环。
中序遍历
递归法
class Solution {
List<Integer> list = new ArrayList<>();
private void minOrder(TreeNode root) {
if (root==null) {
return;
}
minOrder(root.left);
list.add(root.val);
minOrder(root.right);
}
public List<Integer> inorderTraversal(TreeNode root) {
minOrder(root);
return list;
}
}与先序遍历相比,中序遍历只需要将add(0的位置改为在root.left和root.right的中间就行了。
迭代法
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
while (root!=null || !stack.isEmpty()) {
while (root!=null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
list.add(root.val);
root = root.right;
}
return list;
}
}与先序遍历相比中序遍历的迭代也只是改变了add()的位置,因为只有我们的左完了也就是我们的内部的while()循环结束了,我们在弹出元素的时候才能add()同时抢在root=root.right的前面。
后序遍历
递归法
class Solution {
List<Integer> list = new ArrayList<>();
private void beOrder(TreeNode root) {
if (root==null) {
return;
}
beOrder(root.left);
beOrder(root.right);
list.add(root.val);
}
public List<Integer> postorderTraversal(TreeNode root) {
beOrder(root);
return list;
}
}后序遍历的递归法同上我们只需要把add()放在root.right的后面就行了。
迭代法
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
TreeNode prev = null;
while (root!=null || !stack.isEmpty()) {
while (root!=null) {
stack.push(root);
root = root.left;
}
TreeNode ret = stack.peek();
if (ret.right != null && ret.right != prev) {
root = ret.right;
} else {
list.add(ret.val);
stack.pop();
prev = ret;
}
}
return list;
}
}后序遍历的迭代法相对而言就比较麻烦一点,因为我们不能参考前面直接的把add()加在root.right的后面这样的话我们的原root就被弹出去了,然后也不会再次遍历它了,我们找到的只是root的right。
所以这时候我们用了一个ret用于接受我们的栈顶元素,如果我们栈顶元素的所在的节点的右为空的话,因为我们是左右根遍历的,既然右没了那就不需要再去找右了直接把当前的左给list.add()了,如果有右的话就接着 root=root.right 往右传接着探索,这时我们要注意一个bug。
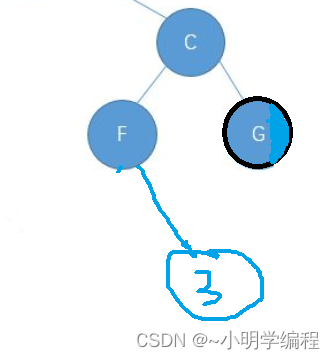
当遇到这种情况的时候,当我们3节点弹出的时候会对F进行操作然后F节点的右不为空又要push()3这个节点,然后就会陷入死循环,这时候就会凸显出来我们prve的作用了,记录上一个弹出的节点只有我们roo.right的节点不是prev我们才会接着遍历它,否则就弹出,同时我们弹出的时候要用prev标记一下这个节点。